Энергия гармонических колебаний

Чтобы придать материальной точке колебательное движение, нужно вывести ее из положения равновесия. Для этого выполняют определенную работу против вращающей силы. Эта работа будет мерой потениальной энергии, сообщенной точке извне:

П=

Потенциальная энергия точки в колебательном движении пропорциональна квадрату смещения.

После остановки действия внешней силы точка будет возвращаться в положение равновесия под действием квазиупругой силы. По мере уменьшения смещения, соответственно закону сохранения энергии , потенциальная энергия точки превращается в кинетическую.

Поскольку смещение точки x= Asin ωt и коэффициент квазиупругой силы k=m ω², то потенциальную энергию точки в колебательном движении можно определить по формуле:

П=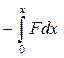=mv₀²x²/2=mA²ω₀²/2·cos²(ω₀t+φ)

П=mA² ω₀²/2[1+cos2(ω₀t+φ)]

E=П+Т=mA²ω₀²/2 Е=const

Кинетическая энергия колеблющейся материаль­ной точки равна:

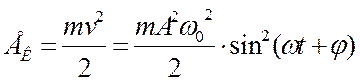
В положении крайнего смещения потенциальная энергия максимальная, а кинетическая равна 0. С движением к положению равновесия потенциальная энергия уменьшается, а кинетическая увеличивается; в момент равновесия потенциальная энергия равна 0, а кинетическая приобретает максимальное значение. За счет кинетической энергии точка дальше смещается в противоположный бок. Такие периодические колебания потенциальной и кинетической энергии происходят в процессе гармонических колебаний.

Полная энергия точки в колебательном движении состоит из суммы потенциальной и кинетической энергии:

Е=П+К=1/2 m ω² А² sin² ωt + 1/2 m ω² А² cos² ωt, или Е= ½ m ω² А²

То есть, энергия точки в колебательном движении пропорциональна квадрату амплитуды и квадрату частоты. Если система изолирована от других внешних вмешательств и точка колеблется без трения, то согласно закону сохранения энергия Е колебательного движения остается постоянной.

Электрический колебательный контур –это электрическая цепь, состоящая из последовательно включенных катушки индуктивности L, конденсатора емкостью С и резистора, сопротивлением R.

По закону Ома для участка цепи IR= φ₁- φ₂ + ЭДС или IR = -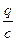-L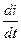, где q и φ₁- φ_{2 =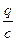} -- заряд конденсатора и вольный момент времени t, R-электрическое сопротивление колебательного контура, ЭДС –ЭДС самоиндукции.

.В момент времени t=0 зарядим конденсатор, при этом на обкладках конденсатора появляются заряды ±Q, следовательно, между обкладками конденсатора имеется электрическое поле, энергия которого равна:

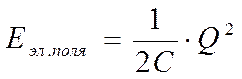
Если конденсатор замкнут на катушку индук­тив­ности L, то он начинает разряжаться и в контуре начинает протекать ток I, который возрастает со временем. При этом заряд конденсатора уменьшается, а энергия магнитного поля: 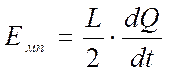возрастает.

Полная энергия контура является суммой этих энергий и постоянна:

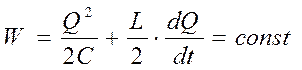
В момент времени t=1/4Т конденсатор полностью разрядится, энергия электрического поля равна 0, а энергия магнитного поля , а следовательно, и ток, достигнут максимума.

Начиняя с момента времени t=1/4Т, ток в контуре уменьшается, магнитное поле начинает ослабевать и в катушке индуцируется ток, который по правилу Ленца течет в том же направлении, что и ток разрядки конденсатор. Конденсатор начнет разряжаться, воз­никнет электрическое поле, ослабляющее ток, кото­рый в конечном счете достигнет 0, и в этот момент заряд на обкладках достигнет максимума. Теперь конденсатор перезаряжен и после этого процессы начнут протекать в обратном направлении и система к моменту времени t=Т вернется в первоначальное состояние.

После этого повторно начнется процесс переза­рядки конденсатора, то есть возникнут электрические колебания, сопровождающиеся превращениями энер­гий электрического и магнитного полей.

Если R=0, то дифференциальное уравнение свободных гармонических колебаний заряда в контуре описывается:

А заряд Q совершает гармонические колебания, которые описываются выражением:

Q=Q_maxcos(ω₀t+φ)

Q_max — максимальный заряд на обкладках конденсатора (амплитуда заряда),

ω₀ — собственная частота колебательного контура.

Она равна:

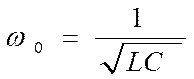
Отсюда период Т=2π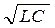- формула Томсона.