Дифференциальное уравнение вынужденных колебаний. Амплитуда и фаза вынужденных колебаний. Резонанс.

Вынужденные колебания — незатухающие колебания реальной колебательной системы, в которой потери энергии компенсируются с помощью каких-либо периодических действующих факторов х(t), причем их действие происходит по гармоническому з-ну:

х=Acos(ω₀t+φ)

В случае механических колебаний роль х(t) выполняет внешняя сила F:

F=F₀-cosωt

Теперь закон движения пружинного маятника принимает вид:

mx′′=-kx-rx′+ F₀cos ωt

Однако, δ=r/2m ω₀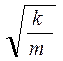

x′′+2δx′+ ω₀²x=(F₀/m)cosωt

В случае эл. колебаний контура роль х(t) выполняет переменноt напряжение:

U=U_mcosωt

δ=R/2L, а ω₀=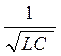

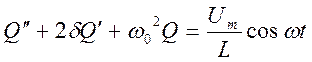
Сводятся к линейному однородному дифферен­ци­альному уравнению типа:

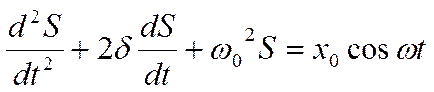
В случае мех. колебаний х₀=F₀/m, а в случае эл. колебаний х₀=U_m/L.

Решение этого уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

S=A₀e^-δtcos(ω₁t+φ₁) — общее решение

S=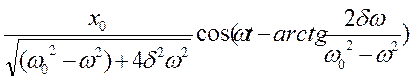— частное решение

Первое слагаемое играет существенную роль в начальной стадии процесса, то есть при установлении колебаний, пока амплитуда вынужденных колебаний не достигнет определенного значения.

На стадии установившихся колебаний А вынуж­денных колебаний достигает значений, определяемых выражением:

А=

На стадии установившихся колебаний они являются гармоническими, происходит с частотой ω, а фаза этих колебаний описывается уравнением:

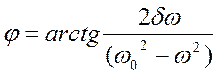
Амплитуда и фаза колебаний зависят от частоты ω.

Из выражения для амплитуды можно сделать вывод, что А имеет максимум. Частота, при которой А достигает максимума значения, называется резо­нанснойи обозначается ω_рез.

Резонанс– явление возрастания амплитуды установившихся вынужденных колебаний до макс. Значения при приближении частоты изменения внешней силы к частоте свободных колебаний сис-мы.

Если продифференцировать подкоренное выраже­ние по ω и для нахождения максимума приравнять его к 0, получим выражение, определяющее ω_рез.

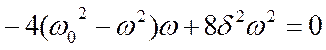
Отсюда

ω_рез=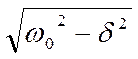

Если δ²<<ω₀², то ω_рез совпдает с собственной частотой ω₀.

Если подставить это выражение в выражение для амплитуды, то получим А в момент резонанса:

А_рез=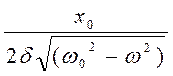

По мере увеличения δ максимум зависимости А от ω смещается в область меньших частот. Высота максимума падает, а сам максимум уширяется.