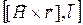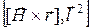Задачи по квантовой механике.
1. Доказать, что оператор градиента является антиэрмитовым на базисе функций, обращающихся в нуль на бесконечности.
2. Доказать равенство [L´L] = iL,где L – оператор орбитального момента.
3. Доказать равенство (s×a)(s ×b)=(a×b)+i(s×[a´b]), где s– матрицы Паули, aиb– произвольные векторы.
4. Рассчитать коммутаторы следующих операторов:
 - некоторый постоянный вектор,
- некоторый постоянный вектор, 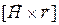 - векторное произведение.
- векторное произведение.
5. Найти среднее значение кинетической энергии в n-состоянии линейного гармонического осциллятора.
6. Найти среднее значение потенциальной энергии в n-состоянии линейного гармонического осциллятора.
7. Найти матрицу оператора x3 на базисе |n> функций линейного гармонического осциллятора.
8. Найти матрицу оператора px3 на базисе |n> функций линейного гармонического осциллятора.
9. Частица находится в потенциальной яме ширины 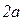 глубины
глубины 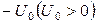 . Определить энергетический спектр, волновые функции локализованных состояний.
. Определить энергетический спектр, волновые функции локализованных состояний.
10. Частица с энергией 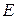 падает на потенциальный барьер высоты
падает на потенциальный барьер высоты 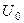
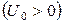 . Определить коэффициент отражения, коэффициент прохождения при
. Определить коэффициент отражения, коэффициент прохождения при 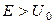 .
.
11. Частица с энергией 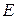 падает на потенциальный барьер высоты
падает на потенциальный барьер высоты 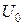
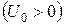 . Определить коэффициент отражения, коэффициент прохождения при
. Определить коэффициент отражения, коэффициент прохождения при 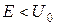 .
.
12. Найти энергетический спектр и волновые функции частицы, движущейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками:
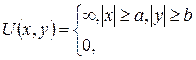
если x<a, y<b.
13. Рассчитать коммутатор [H, r], где H – одночастичный оператор Гамильтона, r - радиус-вектор частицы.
14. Найти распределение вероятностей различных значений импульса в основном состоянии частицы в бесконечно глубокой потенциальной яме.
15. Частица находится в бесконечно глубокой потенциальной яме ширины а: найти вероятность обнаружения частицы в области a/3 £x£2a/3.
16. Волновая функция частицы имеет вид
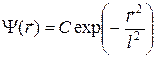 ,
, 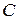 - нормировочная постоянная. Определить распределение вероятностей различных значений импульса в этом состоянии.
- нормировочная постоянная. Определить распределение вероятностей различных значений импульса в этом состоянии.
17. Доказать, что в одномерной потенциальной яме конечной глубины и ширины всегда есть, хотя бы один локальный уровень.
18. Найти энергетический спектр и волновые функции двумерного гармонического осциллятора, описываемого гамильтонианом
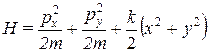 .
.
19. Проверить непосредственным расчётом справедливость теоремы вириала для линейного гармонического осциллятора.
20. Построить оператор, эрмитово сопряжённый к (∂/∂r), где r – радиальная переменная в сферической системе координат.
21. Частица помещена в трёхмерную бесконечно глубокую потенциальную яму (U(x, y, z) = ∞, |x| > a, |y| > b, |z| > c).Определить среднее давление частицы на стенки ямы. Указание: рассмотреть выражение для работы, совершаемой при бесконечно малом изменении объёма области, доступной для частицы.
22. Линейный одномерный гармонический осциллятор, несущий заряд Q, помещён в однородное электрическое поле с напряжённостью E. Найти среднее значение координаты осциллятора в n-м состоянии.
23. Найти среднее значение x2 для линейного гармонического осциллятора, находящегося в своём третьем возбуждённом состоянии.
24. Найти с.з. и нормированные с.ф. оператора ∂/∂j, где j - угловая переменная в полярной системе координат.
25. Определить энергетические уровни дискретного спектра частицы в потенциальной яме: U(x) = ∞, x < 0; 0, 0<x<a; U0, x>a.
26. Вычислить среднее значение оператора 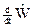 в n-м стационарном состоянии jn гамильтониана:
в n-м стационарном состоянии jn гамильтониана: 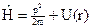 , где
, где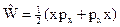 - оператор вириала. Получить отсюда соотношение между средней кинетической и потенциальной энергией для случая U(x) ~ xa (теорема вириала). Указание: учесть, что, по определению, H jn = En jn
- оператор вириала. Получить отсюда соотношение между средней кинетической и потенциальной энергией для случая U(x) ~ xa (теорема вириала). Указание: учесть, что, по определению, H jn = En jn
27. Частица, помещённая в бесконечно глубокую потенциальную яму ширины a (0<x<a), находится в состоянии с волновой функцией Y = A x (x - a). Найти для неё распределение различных значений энергии и среднюю энергию, определив константу A из условия нормировки. Указание: для нахождения распределения энергий рассмотреть ‹Y|jn›, где jn – в.ф. n-го стационарного состояния.
28. Частица, помещённая в бесконечно глубокую потенциальную яму ширины a (0<x<a), находится в состоянии с волновой функцией Y = A sin2(px/a). Найти для неё распределение различных значений энергии и среднюю энергию, определив константу A из условия нормировки. Указание: для нахождения распределения энергий рассмотреть ‹Y|jn›, где jn – в.ф. n-го стационарного состояния.
29. Вычислить коэффициент отражения от потенциального барьера: U = 0, x<0; U0, x>0.
30. Оператор спина электрона (в единицах ħ) имеет вид: 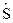 = ½ s, где s=(sx, sy, sz), si – матрицы Паули. Составить оператор Sn проекции спина на ось n. Найти среднее значение Sn в состояниях с Sz = ± ½ ? Каковы вероятности проекций Sn = ± ½ в указанных состояниях?
= ½ s, где s=(sx, sy, sz), si – матрицы Паули. Составить оператор Sn проекции спина на ось n. Найти среднее значение Sn в состояниях с Sz = ± ½ ? Каковы вероятности проекций Sn = ± ½ в указанных состояниях?
31. Проверить непосредственным расчётом справедливость теоремы вириала для линейного гармонического осциллятора.
32. В одномерной потенциальной яме сколь угодно малой глубины всегда имеется по крайней мере одно связанное состояние (один уровень дискретного спектра). Доказать эту теорему для случая симметричной прямоугольной ямы.
33. Рассчитать среднюю величину произведения неопределённостей DxDp для основного состояния линейного гармонического осциллятора (DA = ‹A2› - ‹A›2).
34. Рассчитать среднюю величину произведения неопределённостей DxDp для основного состояния частицы в бесконечно глубокой симметричной потенциальной яме ширины a (DA = ‹A2› - ‹A›2).
35. Найти среднее значение электрического квадрупольного момента в 2pz-состоянии атома водорода.
36. Найти “среднеквадратичное” значение радиуса “орбиты” электрона в 1s-состоянии атома водорода.
37. Рассчитать матрицу электрического дипольного момента электрона на базисе состояний атома водорода с n=2.
38. Найти распределение вероятностей различных значений импульса в основном состоянии атома водорода.
39. Найти средний потенциал поля, создаваемого ядром и электроном в основном состоянии атома водорода.
40. Найти с.з. и с. ф. спинового оператора (S=1)
a)VS= DSz2 +E(Sx2-Sy2)
b)VS= SxSy+SySx (S=1)
c)VS= SxSz+SzSx (S=1)
d)VS= SzSy+SySz (S=1)
41. Найти собственные значения и собственные функции спинового оператора VS= I(S1×S2) (I – «обменный» интеграл).
42. Найти собственные значения и собственные функции спинового оператора VS= D[S1´S2] (D – вектор Дзялошинского) для S1=S2=1/2.
43. Найти собственные функции квадрата и z-компоненты полного момента, являющегося суммой двух моментов S1=S2=1/2.
44. Найти расщепление и волновые функции nl-электрона атома водорода в кристаллическом поле, образованном точечными зарядами: а) 2p-электрон атома, находящегося в центре квадрата из точечных зарядов; б) 2p-электрон атома, находящегося в центре равностороннего треугольника из точечных зарядов; в) 3d-электрон атома, находящегося в центре квадрата из точечных зарядов (см., А.С. Москвин, Ю.Д. Панов, Атомы в кристаллах, УРГУ, 1999) ; г) 3d-электрон атома, находящегося в центре октаэдра из точечных зарядов (см., А.С. Москвин, Ю.Д. Панов, Атомы в кристаллах, УРГУ, 1999) ; д) 3d-электрон атома, находящегося в центре куба из точечных зарядов (см., А.С. Москвин, Ю.Д. Панов, Атомы в кристаллах, УРГУ, 1999) ; е) 3d-электрон атома, находящегося в центре тетраэдра из точечных зарядов (см., А.С. Москвин, Ю.Д. Панов, Атомы в кристаллах, УРГУ, 1999).
45. Рассчитать эффект Зеемана для 3dt2g-электрона с учетом спин-орбитального взаимодействия.
46. Рассчитать вероятность электродипольного 1s-2p перехода в атоме водорода, помещенном в а) однородное электрическое поле, б) неоднородное электрическое поле тетрагональной (ромбической) симметрии, в) однородное магнитное поле.
47. Рассчитать поляризуемость атома водорода в основном состоянии.
48. Найти поправки к энергии и правильные линейные комбинации для N-кратно вырожденного уровня, если матрица оператора возмущения имеет вид: <i|V|j>=d, i,j=1,2, …N (см. Ч. Китель, Введение в физику твердого тела, М., 1978, стр.757-760).