Основные задачи динамики материальной точки
В проекциях на оси декартовой системы координат векторное равенство (4.1) в общем случае криволинейного движения точки в пространстве запишется в виде
 ,
, 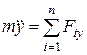 ,
, 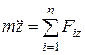 , (4.2)
, (4.2)
где 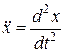 ,
, 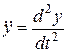 ,
,  – проекции ускорения точки
– проекции ускорения точки 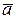 ;
; 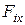 ,
, 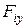 ,
, 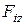 –проекции силы
–проекции силы 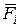 на соответствующие оси координат, которые могут быть функциями времени t положения точки x, y, z и проекцией
на соответствующие оси координат, которые могут быть функциями времени t положения точки x, y, z и проекцией 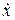 ,
, 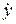 ,
, 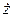 скорости
скорости 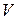 .
.
Уравнения (4.2) образуют систему дифференциальных уравнений движения материальной точки в координатной форме. При заданной траектории точки ее дифференциальные уравнения движения в проекциях на естественные оси криволинейной траектории записываются в виде
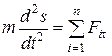 ,
, 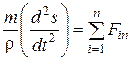 ,
,  , (4.3)
, (4.3)
где s – дуговая координата, определяющая положение точки на траектории; ρ – радиус кривизны траектории в данной точке; 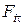 ,
, 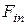 ,
, 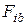 – проекции силы
– проекции силы 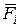 на естественные оси траектории: касательную
на естественные оси траектории: касательную 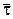 , нормаль
, нормаль 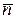 , бинормаль
, бинормаль 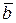 .
.
На практике выделяют две основные задачи динамики свободной материальной точки, решаемые с помощью уравнений (4.2) или (4.3):
Первая задача (прямая) – считая заданным движение материальной точки массой m, определить равнодействующую сил, вызывающих это движение.
Вторая задача (обратная) – определить движение, которое будет совершать точка массы m под действием заданных сил.
При решении прямой задачи, например с помощью уравнений (4.2), нужно дважды продифференцировать заданные уравнения движения точки, подставить полученные проекции ускорения точки в уравнения (4.2) и определить равнодействующую сил, действующих на точку.
Для решения обратной задачи необходимо найти решение дифференциальных уравнений (4.2). Аналитически обратная задача решается только в частных случаях. Если аналитическое решение невозможно, задача решается численно.
Если систему уравнений (4.2) удастся один раз проинтегрировать, то полученные новые зависимости будут включать время, координаты, их первые производные и три константы интегрирования С1, С2, С3:
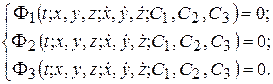 (4.4)
(4.4)
Систему (4.4) называют системой первых интегралов уравнений динамики точки.
Если систему (4.4) удастся проинтегрировать еще раз, то полученное решение будет зависеть еще от 3 констант интегрирования С4, С5, С6:
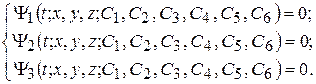 (4.5)
(4.5)
Для определения констант интегрирования используют начальные условия, которые задают начальное положение точки 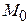 (
(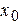 ,
, 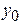 ,
, 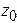 ) и ее начальную скорость
) и ее начальную скорость 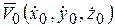 в момент времени t = t0:
в момент времени t = t0:
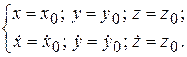 (4.6)
(4.6)
Подставляя начальные условия (4.6) в выражения (4.4) и (4.5), составляют шесть уравнений для определения констант интегрирования:
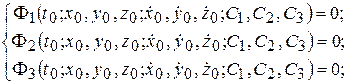
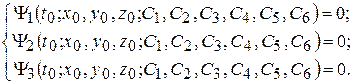
После определения констант интегрирования решение задачи, соответствующее заданным начальным условиям (4.6), записывается в виде
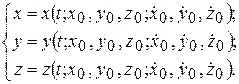
В случае несвободного движения материальной точки уравнения (4.2) и (4.3) будут содержать также неизвестные проекции реакций связей и число неизвестных в общем случае будет превышать число уравнений, Для того чтобы обратная задача была разрешимой, необходимы дополнительные сведения о характере наложенных на материальную точку связей.