Туннельный эффект
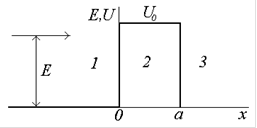
Большой интерес вызывает задача прохождения частицы через потенциальный барьер конечной протяжности. Определим коэффициент прозрачности  высокого барьера, когда
высокого барьера, когда  (рис.1.3). Частицы падают на барьер, двигаясь в положительном направлении оси
(рис.1.3). Частицы падают на барьер, двигаясь в положительном направлении оси  . Используя результаты предыдущего параграфа, определим волновую функцию в трех областях
. Используя результаты предыдущего параграфа, определим волновую функцию в трех областях
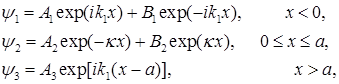 (1.93)
(1.93)
где 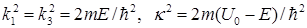 .
.
Из требования непрерывности волновой функции и ее первой производной в точках скачка потенциальной энергии ( и
и  ) получим систему алгебраических уравнений:
) получим систему алгебраических уравнений:
 (1.94)
(1.94)
Решим (1.94) относительно  :
:
 . (1.95)
. (1.95)
Амплитуда плоской волны оказывается отличной от нуля в области за барьером, невзирая на то, что энергия частицы меньше высоты барьера  . Это означает, что микрочастица с определенной вероятностью может пройти через потенциальный барьер путем туннельного перехода.
. Это означает, что микрочастица с определенной вероятностью может пройти через потенциальный барьер путем туннельного перехода.
Коэффициент прохождения микрочастиц через барьер определяется следующим образом
 . (1.96)
. (1.96)
Здесь использовано тождество
 .
.
Если  , то
, то  и выражение (1.96) упрощается
и выражение (1.96) упрощается
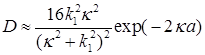 . (1.97)
. (1.97)
Основная зависимость коэффициента прохождения от высоты и ширины барьера определяется экспоненциальным множителем. Обозначив предэкспоненциальный множитель как  , имеем
, имеем
 . (1.98)
. (1.98)
| 
|
| а | б |
| Рис.1.3. Энергетическая диаграмма потенциального барьера (а) и зависимость коэффициента прозрачности барьера для электронов с энергией Е от ширины барьера (б) |
Из (1.98) видно, что вероятность прохождения микрочастицы через барьер не очень мала, если
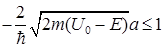 . (1.99)
. (1.99)
Это условие может выполняться только в области микромира. На рис.1.3, б приведена зависимость коэффициента  от ширины барьера.
от ширины барьера.
Формулу (1.98), полученную для прямоугольного потенциального барьера, можно обобщить на случай барьера произвольной формы  (рис.1.4).
(рис.1.4).
Такой барьер можно приближенно представить как совокупность элементарных прямоугольных барьеров шириной  и высотой
и высотой 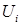 . Частица с энергией
. Частица с энергией 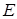 , входит в барьер в точке
, входит в барьер в точке 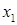 и выходит из него в точке
и выходит из него в точке 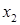 . Вероятность прохождения отдельного элементарного барьера определяется формулой (1.98)
. Вероятность прохождения отдельного элементарного барьера определяется формулой (1.98)
 .
.

|
Рис.1.4. Энергетическая диаграмма потенциального барьера произвольной формы  . .
|
Поскольку эти события независимы, вероятность прохождения всего барьера будет определяться произведением вероятностей прохождения всех его составляющих, то есть
 (1.100)
(1.100)
Перейдя в (1.100) от суммирования к интегрированию, получим
 , (1.101)
, (1.101)
где  .
.
Прохождение частиц сквозь потенциальные барьеры на первый взгляд выглядит парадоксальным. Эту парадоксальность видят в том, что частица, которая находится внутри потенциального барьера с полной энергией 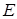 , которая меньше высоты барьера, должна иметь отрицательную кинетическую энергию
, которая меньше высоты барьера, должна иметь отрицательную кинетическую энергию 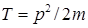 , потому что полная энергия согласно классической механике есть сумма кинетической и потенциальной
, потому что полная энергия согласно классической механике есть сумма кинетической и потенциальной
 . (1.102)
. (1.102)
В области, где  ,
, 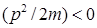 , что не имеет смысла, поскольку импульс есть действительная величина. Это те области, которые согласно законам классической механики недоступные для частицы. Согласно же законам квантовой механики частица может находиться в этой «запрещенной» области. Таким образом, выходит, что квантовая механика допускает возможность отрицательной кинетической энергии и, как следствие, мнимого импульса частицы. Этот вывод и называют «парадоксом туннельного эффекта».
, что не имеет смысла, поскольку импульс есть действительная величина. Это те области, которые согласно законам классической механики недоступные для частицы. Согласно же законам квантовой механики частица может находиться в этой «запрещенной» области. Таким образом, выходит, что квантовая механика допускает возможность отрицательной кинетической энергии и, как следствие, мнимого импульса частицы. Этот вывод и называют «парадоксом туннельного эффекта».
В действительности здесь нет никакого парадокса, а сам вывод неверен. Дело в том, что туннельный эффект представляет собой чисто квантовое явление и поэтому он может обсуждаться только в рамках квантовой механики (при переходе к классической механике (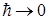 ) туннелирование исчезает). Полную энергию частицы можно рассматривать как сумму кинетической и потенциальной энергии только на основе классической механики. Формула (1.102) допускает, что мы одновременно знаем величину как кинетической
) туннелирование исчезает). Полную энергию частицы можно рассматривать как сумму кинетической и потенциальной энергии только на основе классической механики. Формула (1.102) допускает, что мы одновременно знаем величину как кинетической 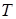 , так и потенциальной энергии
, так и потенциальной энергии  . Другими словами, мы приписываем одновременно определенное значение координате частицы
. Другими словами, мы приписываем одновременно определенное значение координате частицы  и ее импульсу
и ее импульсу 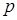 , что противоречит законам квантовой механики (принципу неопределенностей). Разделение полной энергии на потенциальную и кинетическую в квантовой механике невозможно, а, следовательно, безоснователен и сам парадокс, который базируется на возможности представить полную энергию
, что противоречит законам квантовой механики (принципу неопределенностей). Разделение полной энергии на потенциальную и кинетическую в квантовой механике невозможно, а, следовательно, безоснователен и сам парадокс, который базируется на возможности представить полную энергию 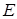 как сумму кинетической энергии (функция импульса) и потенциальной энергии (функция координат).
как сумму кинетической энергии (функция импульса) и потенциальной энергии (функция координат).
Обнаружить частицу внутри потенциального барьера действительно возможно, даже при  . Но когда фиксируется координата частицы, то при этом создается, согласно соотношению неопределенности, дополнительная дисперсия импульса
. Но когда фиксируется координата частицы, то при этом создается, согласно соотношению неопределенности, дополнительная дисперсия импульса 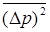 , так что уже нельзя утверждать, что энергия частицы, после того как определили ее положения, равняется
, так что уже нельзя утверждать, что энергия частицы, после того как определили ее положения, равняется 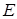 .
.
Как было показано в разд. 1.10, неопределенность энергии частицы, которая локализована в области под барьером, больше той энергии, которой ей не хватает до высоты барьера.
Туннелирование электронов сквозь потенциальный барьер объясняет известное явление автоэлектронной эмиссии. Если к металлу приложить большое электрическое поле (( ) так, чтобы он был катодом, то такое поле вырывает электроны из металла и возникает электрический ток.
) так, чтобы он был катодом, то такое поле вырывает электроны из металла и возникает электрический ток.
Возьмем за основу модель свободных электронов. Будем считать, что потенциальная энергия электронов внутри металла равняется нулю. Металл для электронов можно рассматривать как потенциальную яму, энергетические уровни которой они заполняют вплоть до уровня Ферми[28] 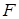 (при Т=0 К) (рис.1.4). Поскольку максимальная энергия электронов
(при Т=0 К) (рис.1.4). Поскольку максимальная энергия электронов 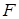 меньше глубины ямы
меньше глубины ямы  , то из-за отсутствия электрического поля электроны практически не выходят за пределы ямы (металла), потому что уровень вакуума представляет для электронов бесконечный потенциальный барьер.
, то из-за отсутствия электрического поля электроны практически не выходят за пределы ямы (металла), потому что уровень вакуума представляет для электронов бесконечный потенциальный барьер.
Приложим электрическое поле 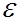 нормально к поверхности металла. Тогда потенциальная энергия электрона будет составлять
нормально к поверхности металла. Тогда потенциальная энергия электрона будет составлять
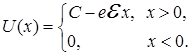 (1.103)
(1.103)

|
| Рис.1.4. Потенциальный барьер на границе металл-вакуум |
Таким образом, на границе металл-вакуум возникает потенциальный барьер треугольной формы. Вычислим коэффициент прозрачности такого барьера для электронов с энергией Ферми 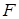 . Для этого воспользуемся формулой (1.101), обозначив показатель экспоненты как
. Для этого воспользуемся формулой (1.101), обозначив показатель экспоненты как
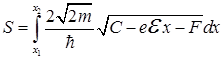 . (1.104)
. (1.104)
Первую точку поворота принимаем за нуль 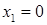 , вторая определяется из рис.1.4:
, вторая определяется из рис.1.4:
 . (1.105)
. (1.105)
Введем новую переменную  и вычислим (1.104):
и вычислим (1.104):
 . (1.106)
. (1.106)
Введя обозначение 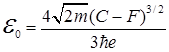 , получим для коэффициента прозрачности
, получим для коэффициента прозрачности
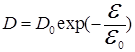 , (1.107)
, (1.107)
где  и
и 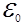 – постоянные, которые зависят от типа металла.
– постоянные, которые зависят от типа металла.
Плотность тока автоэлектронной эмиссии будет составлять
 . (1.108)
. (1.108)
Эта зависимость тока от поля подтверждается экспериментами.