Калорические коэффициенты

Внутренняя энергия системы U, будучи функцией состояния, является функцией независимых переменных (параметров состояния) системы.

В простейших системах будем рассматривать внутреннюю энергию как функцию двух переменных — объёма и температуры:

U = f (V, T) (I, 23)

Третья переменная (давление) в этом случае является зависимой переменной и однозначно определяется из уравнения состояния по значениям первых двух.

Тогда полный дифференциал dU будет равен:

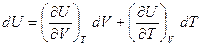(1, 24)

Подставив значение dU из уравнения (I, 24) в уравнение (I, 9), находим:

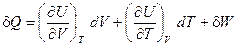(I, 25)

Если в изучаемой системе имеет место только работа расширения и отсутствуют работы электрическая, силы тяготения, поверхностных сил и т. д., то dW = PdV. Тогда

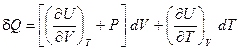(I, 26)

Обозначив коэффициенты при дифференциалах независимых переменных в уравнении (I, 26) символами l и C_V , получим:

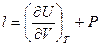(I, 27)

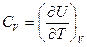(I, 28)

Тогда окончательно получим:

δQ = ldV + C_VdT (1, 29)

Коэффициент l, размерность которого совпадает с размерностью давления, складывается из внешнего давления и члена 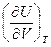, который отражает взаимное притяжение молекул. Слагаемое 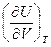мало для реальных газов и очень велико (по сравнению с обычными значениями внешнего давления) для жидкостей и твёрдых тел.

Для δQ запишем выражение, аналогичное (I, 24):

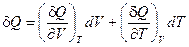(I, 30)

Т. к. в уравнениях (I, 26) и (I, 30) равны левые части, то равны и правые части:

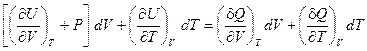
Поскольку V и T — независимые переменные, коэффициенты при соответствующих дифференциалах в правой и левой частях уравнения равны (так называемый метод сравнения коэффициентов). Следовательно:

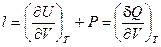и

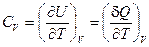
Нетрудно заметить, что C_V есть не что иное, как теплоёмкость при постоянном объёме, что следует из определения (I, 16).

Коэффициент l характеризует теплоту изотермического расширения или, иначе говоря, он равен теплоте, необходимой для изменения объёма системы на единицу при T = const.

Выбрав в качестве независимых переменных P и Т, аналогично можно получить:

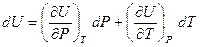
Тогда:

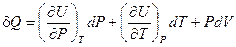(I, 31)

Чтобы избавиться от dV, объём также представим как функцию Р и Т:

V = f (P,T).

Тогда:

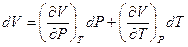(I, 32)

Подставив полученное выражение в (I,31), получим:

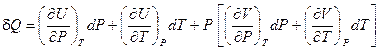
Раскрыв скобки и сгруппировав слагаемые, имеем:

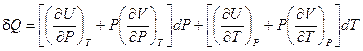(I, 33)

Введём обозначения, как мы уже делали ранее:

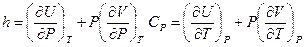(I, 34)

Тогда окончательно имеем:

dQ = hdP + C_PdT (I, 35)

Уравнение, аналогичное (I, 30) запишется в следующем виде:

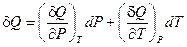
Сравнив его с уравнением (I, 33), получим:

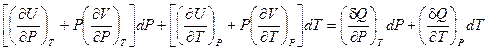
Поскольку P и T — независимые переменные, коэффициенты при соответствующих дифференциалах в правой и левой частях уравнения равны. Следовательно:

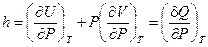и 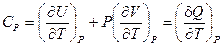(I, 36)

C_P в соответствии с определением (I, 16) есть теплоёмкость при постоянном давлении.

Коэффициент h характеризует теплоту изотермического сжатия или, иначе говоря, он равен теплоте, необходимой для изменения давления системы на единицу при T = const.

Он является существенно отрицательной величиной.

Попробуем найти ответ на ещё один важный вопрос — о соотношении между C_P и C_V . Для этого используем уравнения (I, 29) и (I, 35).

δQ = ldV + C_VdT

dQ = hdP + C_PdT

Т. к. левые части этих уравнений равны, можно приравнять и их правые части:

ldV + C_VdT = hdP + C_PdT (I, 37)

Из трёх переменных P,V и T одна есть функция двух других. Рассматривая объём V как функцию P и T (мы уже делали это ранее): 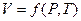, используем выражение для полного дифференциала dV (I, 32). Тогда получим:

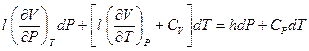
Так как P и T — независимые переменные, коэффициенты при соответствующих дифференциалах в правой и левой частях уравнения равны. Следовательно:

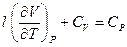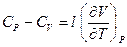или и 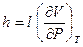(I, 38)

Следует отметить, что для конденсированных (твердых или жидких) фаз их объём очень мало зависит от температуры, следовательно, производная 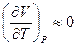и разность C_P – C_V 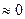, поэтому изобарная и изохорная теплоёмкости в указанном случае практически равны C_P ≈ C_V .

Коэффициенты l, h, C_V, и C_P называются калорическими коэффициентами. Имея самостоятельный физический смысл (особенно C_P, C_V и l), они являются также полезными вспомогательными величинами при термодинамических выводах и расчётах.