Формула полной вероятности и Байеса.
Пусть 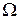 - пространство элементарных событий с алгеброй случайных событий
- пространство элементарных событий с алгеброй случайных событий 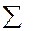 .
.
Определение. Говорят, что случайные события 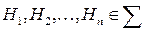 образуют полную группу событий, если они попарно несовместны (то есть
образуют полную группу событий, если они попарно несовместны (то есть 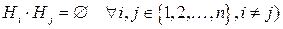 и
и
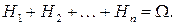
Такие случайные события называют также гипотезами. Заметим, что для полной группы событий 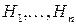 из аксиом 2, 3 следует, что
из аксиом 2, 3 следует, что
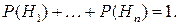
Теорема.Пусть 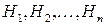 полная группа событий. Тогда
полная группа событий. Тогда
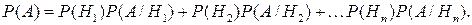 (5)
(5)
Доказательство.
Так как 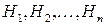 полная группа событий, то не трудно доказать, что
полная группа событий, то не трудно доказать, что
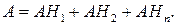
При этом события 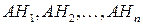 как и события
как и события 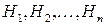 попарно несовместны. Из последнего равенства, аксиомы 3 и формулы (2) следует (5). Теорема доказана.
попарно несовместны. Из последнего равенства, аксиомы 3 и формулы (2) следует (5). Теорема доказана.
Формула (5) называется формулой полной вероятности.
Пример. В первой урне находится три белых и четыре черных шара, а во второй – пять белых и два черных. Из первой урны во вторую перекладывается один шар. Какова вероятность того, что шар, вынутый наугад из второй урны, окажется белым?
Решение.
Обозначим искомое событие через 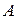 . Состав второй урны зависит от того, какой шар переложили из первой урны.
. Состав второй урны зависит от того, какой шар переложили из первой урны.
Обозначим через 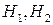 случайные события, состоящие в том, что из первой урны переложен белый и черный шары соответственно. Очевидно, что
случайные события, состоящие в том, что из первой урны переложен белый и черный шары соответственно. Очевидно, что 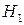 и
и 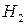 составляют полную группу событий. Найдем
составляют полную группу событий. Найдем
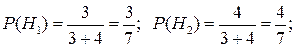
Если переложили белый шар (то есть верна гипотеза 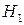 ), то во второй урне окажется 6 белых и 2 черных шара. Поэтому
), то во второй урне окажется 6 белых и 2 черных шара. Поэтому
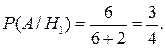
Аналогично,
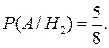
По формуле полной вероятности
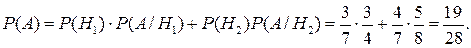
В качестве следствия из формулы полной вероятности выведем формулу Байеса, которая в некотором смысле решает обратную задачу. Пусть 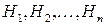 полная группа событий. Допустим, что в результате некоторого опыта наступило случайное событие
полная группа событий. Допустим, что в результате некоторого опыта наступило случайное событие 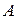 . Требуется найти вероятности выполнения гипотез
. Требуется найти вероятности выполнения гипотез 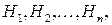 то есть вычислить
то есть вычислить
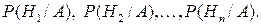
Найдем вероятность 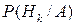 , где
, где 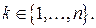 Из формулы (2) следуют равенства
Из формулы (2) следуют равенства
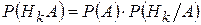 ;
; 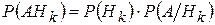 ;
;
Приравнивая правые части, получим
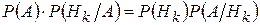 ;
; 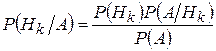 .
.
Выразив P(A) по формуле полной вероятности, выведем формулу
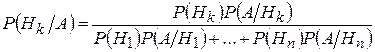 ,
,
которая называется формулой Байеса.
Тема 3: Схема Бернулли. Формулы Муавра-Лапласа.