Принятие решений в условиях определенности.
Детерминированные задачи принятия решений – задачи, в которых состояние среды известно и поэтому сводятся к определению стратегии доставляющей экстремум целевой функции, т. е. к задачам нахождения экстремума целевой функции. Такие задачи называют задачами оптимизации.
В задачах оптимизации без неопределенностей наиболее простая ситуация возникает, когда целевая функция есть функция одной переменной. В этом случае выбор осуществляется по одному критерию, и для принятия решения необходимо установить, существует ли оптимальное решение и как его найти.
Когда множество допустимых альтернатив конечно, решение существует (в конечном множестве всегда существует наибольший и наименьший элементы) и его можно найти методом прямого перебора элементов. Трудности возникают лишь из-за обширности множества альтернатив.
Когда множество альтернатив бесконечно, ответ зависит от свойств этого множества и свойств целевой функции. В приложениях задача нахождения оптимального решения сводится к задаче нахождения экстремума функции одной переменной в некоторой допустимой области. Для нахождения экстремума функции нужно продифференцировать ее по аргументам, приравнять производные нулю и решить полученную систему уравнений. В результате будут найдены критические точки функции, среди которых и находятся точки экстремума.
Таким образом, в рассматриваемом случае задача отыскания оптимального решения сводится к задаче поиска экстремума функции W, она может быть весьма сложной, но возникающие трудности не являются принципиальными, они всегда могут быть преодолены вычислительными средствами.
Поиск оптимальных решений для функций многих переменных в принципе аналогичен поиску оптимального решения для функции одной переменной, но реализация может быть существенно сложнее. В качестве примера рассмотрим задачу: необходимо найти экстремум целевой функции  в области, где
в области, где 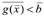 , xi ≥ 0.
, xi ≥ 0.
Максимальное значение  , если оно существует, может быть в точках, принадлежащих множеству внутренних точек области допустимых решений, в которых все частные производные функции f равны нулю, множеству точек границы допустимой области и множеству точек допустимой области, где функция не дифференцируема. Для решения таких задач не существует единого эффективного алгоритма. Поэтому алгоритмы разрабатываются для отдельных типов задач. Методы принятия решений в задачах без неопределенностей достаточно подробно рассматриваются в курсе математического анализа.
, если оно существует, может быть в точках, принадлежащих множеству внутренних точек области допустимых решений, в которых все частные производные функции f равны нулю, множеству точек границы допустимой области и множеству точек допустимой области, где функция не дифференцируема. Для решения таких задач не существует единого эффективного алгоритма. Поэтому алгоритмы разрабатываются для отдельных типов задач. Методы принятия решений в задачах без неопределенностей достаточно подробно рассматриваются в курсе математического анализа.
Рассмотрим теперь задачу нахождения оптимального решения при заданных ограничениях. Пусть требуется найти экстремум функции f (x1, x2,..., xn) при условиях

Эти условия определяют область D допустимых решений. Для решения таких задач применяют известный метод неопределенных множителей Лагранжа. Точка условного экстремума является стационарной точкой функции Лагранжа

где λj – переменные, называемые множителями Лагранжа.
Обычно предполагается, что n > m и разность n-m называют числом степеней свободы данной задачи. В прикладных задачах f (x1, x2,..., xn) часто интерпретируется как доход или стоимость, а правые части bi, i = 1,2,...,m - как затраты некоторых ресурсов. Тогда множители i – отношение единицы стоимости к единице ресурса с номером i. Они показывают, как изменится максимальный доход или стоимость, если количество ресурса с номером i увеличится на единицу.
Таким образом, для нахождения условного экстремума необходимо решить систему уравнений, полученную приравниванием нулю всех частных производных функции Лагранжа. Например, для функции f(x,y) при одном условии (ограничении) g(x,y) = 0 функция Лагранжа имеет вид
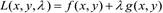
Следовательно, ищется экстремум функции f(x,y) на линии, уравнение которой g(x,y) = 0.
Система уравнений необходимая для нахождения условного экстремума имеет вид