Принятие решений в условиях конфликта.
Задачи принятия решений в условиях конфликта изучаются в теории игр. Участвующие в конфликте стороны заинтересованы в том, чтобы скрыть от противника свои намерения. Основой теории игр является формализация понятий конфликта, принятия решения в нем и полезности (оптимальности) этого решения.
Участников конфликта называют игроками, их возможные действия – стратегиями, исходы конфликта – ситуациями, заинтересованные стороны – участники конфликта, сущность заинтересованности – возможные предпочтения одной ситуации перед другой для каждого игрока. Конкретизация этих понятий приводит к разнообразным частным классам игр.
Принятием решения в теории игр считается выбор игроком своей стратегии. Вопрос о формализации понятия полезности (оптимальности) принимаемого решения является сложным. Единого представления о нем нет, и поэтому рассматриваются разные версии, но в основе каждой из них лежит интуитивное представление о полезности, как о чем-то устойчивом и справедливом. Формализация этих представлений определяется системой аксиом.
Ситуации, удовлетворяющие в игре требованиям полезности (оптимальности), называются решениями игры. Ограничимся рассмотрением игр двух участников с прямо противоположными (антагонистическими) интересами. Формально эта противоположность выражается в том, что при переходе от одной ситуации к другой увеличение выигрыша одного игрока влечет численно равное уменьшение выигрыша другого. Сумма выигрышей игроков в любой ситуации постоянна (ее можно считать равной нулю). Существует много явлений, для которых антагонистические игры являются хорошей моделью. Например, некоторые военные операции, спортивные игры, деловые решения в условиях конкуренции и т.д.
Антагонистическая игра задается множествами A и B стратегий игроков и вещественной функцией H, определенной на множестве A × B и являющейся функцией выигрыша первого игрока (функция выигрыша второго игрока равна –H). Процесс игры состоит в выборе игроками некоторых своих стратегий a ∈ A, b∈ B, после чего первый игрок получает от второго сумму H(a, b). Разумное (осторожное) поведение игроков в антагонистической игре осуществляется на основании принципа максимина.
Если

то у каждого игрока существует оптимальная осторожная стратегия. Эта стратегия называется «чистой» стратегией. Однако уже в самых простых ситуациях принцип максимина может не выполняться.
Если множества A и B конечны, то антагонистическая игра называется матричной игрой. Для нее всегда существуют оптимальные смешанные стратегии у обоих игроков. Если первый игрок имеет m стратегий, а второй – n стратегий, то матричная игра может быть задана m × n матрицей A = {ai,j}.
Для решения матричной игры необходимо найти оптимальные стратегии игроков и цену игры. Практическое правило для решения матричной игры следующее. К платежной матрице A добавим один столбец справа и одну строку снизу. В ячейки столбца запишем минимальное значение платежа соответствующей строки, а в ячейки строки – максимальное значение соответствующего столбца (таблица).
Таблица. Решение матричной игры
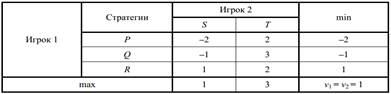
Первый игрок будет выбирать стратегию, которая гарантирует ему максимальный выигрыш независимо от выбора стратегии второго игрока. Поэтому он выберет стратегию, при которой он будет иметь максимальный выигрыш из возможных минимальных выигрышей (в столбце min это элемент, соответствующий стратегии R первого игрока), т. е. гарантированный выигрыш первого игрока:
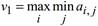
Этот выигрыш v1 называют нижней ценой игры, а соответствующую стратегию – максиминной стратегией первого игрока.
Второй игрок, стараясь минимизировать проигрыш, выберет стратегию, гарантирующую наименьший из максимально возможных проигрышей, т. е. стратегию i j

которую называют минимаксной стратегией. Число v2 называют верхней ценой игры. Если v1 = v2 = v, то число v называют ценой игры. Игры, для которых v1 = v2 = v, называют играми с седловой точкой. Седловых точек может быть несколько. Однако цена игры во всех седловых точках одна и та же. Если один из игроков применяет стратегию, соответствующую одной из седловых точек, то при этом ему обеспечен выигрыш не меньше цены игры. Если и второй игрок применяет стратегию, соответствующую какой-либо седловой точке, то и ему обеспечен проигрыш не более цены игры. Одностороннее отклонение от седловой точки невыгодно ни одному из игроков. Такое отклонение может в лучшем случае оставить выигрыш (проигрыш) неизменным, а в худшем случае – уменьшить (увеличить) его. Таким образом, в играх с седловой точкой оптимальные стратегии обладают своеобразной устойчивостью: если один из игроков применяет свою оптимальную стратегию, то для другого всегда невыгодно отклоняться от своей оптимальной стратегии.
Если в игре участвует много игроков, то каждый игрок с номером i стремится сделать такой выбор, чтобы максимизировать свою целевую функцию fi (свой выигрыш). Но значения целевой функции зависят и от выбора других игроков, т.е.
fi = fi(x1, x2, …, xn)
Если в точке 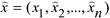 выполняется условие
выполняется условие

то говорят, что в этой точке имеется ситуация равновесия и эту точку называют точкой равновесия в игре. Эти точки также называют точками устойчивости, поскольку, если игрок с номером i выберет стратегию, отличную от 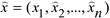 , то при условии, что остальные игроки сохранят свой выбор, проиграет, прежде всего, игрок с номером i, так как
, то при условии, что остальные игроки сохранят свой выбор, проиграет, прежде всего, игрок с номером i, так как

Это значит, что выигрыш каждого игрока в ситуации равновесия не меньше выигрыша, соответствующего другим возможным ситуациям, т. е. отступать от стратегии равновесия невыгодно ни одному из игроков.
Смешанной стратегией называют n-мерный вероятностный вектор p, координаты которого неотрицательны и сумма их равна 1. Значения координат вектора интерпретируются как вероятности выбора стратегии. Смешанные стратегии реализуются случайным выбором чистых стратегий с вероятностями, заданными в векторе p. Например, пусть для первого игрока смешанная стратегия задана вектором (x1, x2,…, xn), а для второго – вектором (y1, y2,…, ym). Так как какая-то из стратегий обязательно реализуется, то
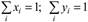
Это значит, что первый игрок будет выбирать стратегию c номером i с вероятностью xi, а второй игрок – стратегию с номером j с вероятностью yj. Полагая, что игроки выбирают стратегии независимо друг от друга, вероятность события (i, j) очевидно равна pi,j = xi yj.
В результате применения смешанных стратегий выигрыш (проигрыш) становится случайной величиной:
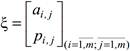
Математическое ожидание этой случайной величины и есть выигрыш (проигрыш) первого (второго) игрока в смешанных стратегиях (x, y):
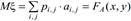
Следовательно, исходной платежной матрице A соответствует новая платежная матрица FA(x, y) игры в смешанных стратегиях. В теории игр доказано, что игра в смешанных стратегиях всегда имеет седловую точку, т.е. такая игра всегда имеет цену, и каждый игрок имеет оптимальную смешанную стратегию.
Наиболее простые конечные игры имеют размерность 2 × 2 и 2 × m. Рассмотрим игру 2 × 2 без седловой точки с матрицей (таблица).
Таблица. Матрица игры

Требуется найти оптимальную смешанную стратегию игрока A:

Эта стратегия имеет свойство: при любых полезных стратегиях противника выигрыш будет равен цене игры υ. В игре 2 × 2 обе стратегии противника – полезные, так как иначе игра имела бы решение в чистых стратегиях (седловую точку). Следовательно, если игрок A придерживается своей оптимальной стратегии, то игрок B может пользоваться любой из своих чистых стратегий и при этом цена игры не изменится. Поэтому можем записать систему уравнений:
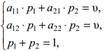
из решения которой найдем

Для определения оптимальной смешанной стратегии игрока B, при известной цене игры, достаточно двух уравнений
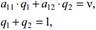
из решения которых получим
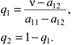
В общем случае решение игры m × n довольно трудная задача. Доказано, что у любой конечной игры m × n имеется решение, число полезных стратегий в котором не превосходит наименьшего из чисел m или n. Трудности решения связаны главным образом с большим объемом вычислений. Поэтому при решении игр m × n применяют аналитические методы линейного программирования.
Рассмотрим сведение игры двух лиц с нулевой суммой к задаче линейного программирования.
Предположим, что цена игры положительна, т.е. ν > 0. Если в платежной матрице имеются отрицательные элементы, то необходимо к платежной матрице прибавить положительное число d, такое, чтобы все ее элементы стали положительными. При этом оптимальные стратегии игроков не изменяются, и цена игры увеличится на d. Применяя оптимальную смешанную стратегию, первый игрок стремится при любой стратегии второго игрока получить выигрыш не менее цены игры ν, которая была бы максимальной. Такая ситуация может быть представлена моделью линейного программирования:

После решения этой задачи находят цену игры:
ν = 1 / (x1 + x2 + …+ xm)
и оптимальную смешанную стратегию для первого игрока.
Если исходная матрица увеличивалась на d, то для получения цены исходной игры значение ν нужно уменьшить на d.
Обозначим
yj = qj / ν
Так как второй игрок старается минимизировать свой проигрыш, его поведение опишем двойственной задачей:
y1 + y2 + …+ yn → max,
Σaji ⋅ yj ≥ 1, i =1, 2, …, m, j = 1, 2, …n, xi ≥ 0.
Таким образом, принятие решения в конфликтной ситуации может быть сведено к двойственной задаче линейного программирования.