С использованием теоремы об изменении кинетической энергии механической системы
Изобразим расчетную схему (рис. 2)
Рис. 2. Расчетная схема
На рис. 2 обозначено:
Р1,Р2,Р3 ,Р4 – силы тяжести,
N4 – нормальные реакции опорной плоскости,
Fуп – упругая реакция пружины,
Х3, У3 – реакции подшипника блока 3,
R=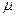 V – сила вязкого сопротивления,
V – сила вязкого сопротивления, 
F(t) – возмущающая сила.
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 3 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1.
Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:
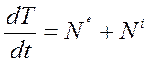 , (1.1)
, (1.1)
где Т - кинетическая энергия системы,
 - сумма мощностей внешних сил,
- сумма мощностей внешних сил,
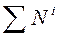 - сумма мощностей внутренних сил.
- сумма мощностей внутренних сил.
Теорема (1.1) формулируется так: "Производная по времени от кинетической энергии механической системы равна алгебраической сумме мощностей внешних и внутренних сил, действующих на точки механической системы".
Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1-3:
Т=Т1+Т2+Т3 +Т4. (1.2)
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
Т1= (1.3)
(1.3)
Каток 2 совершает плоскопараллельное движение, поэтому его кинетическая энергия определяется по теореме Кенига
T2= +
+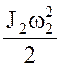 , (1.4)
, (1.4)
где V2 – скорость катка 2
JO2 - момент инерции относительно центральной оси блока;
 - угловая скорость блока.
- угловая скорость блока.
Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия
T3= , (1.5)
, (1.5)
где J3 - момент инерции относительно центральной оси катка,
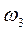 - угловая скорость катка.
- угловая скорость катка.
Блок 4 совершает плоское движение.
T= ,
,
где m4 – масса блока 4,
V4 – скорость блока 4
Кинетическая энергия всего механизма будет равна:
T=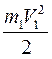 +
+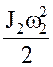 +
+ +
+  (1.6)
(1.6)
Выразим V3, V4,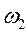 ,
, 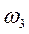 , J2, J3 через скорость груза 1.
, J2, J3 через скорость груза 1.
Положив V1=V=V2, получим
J3=m3i32, J2= ,
,  ,V4=
,V4=

 ,
,  , (1.7)
, (1.7)
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
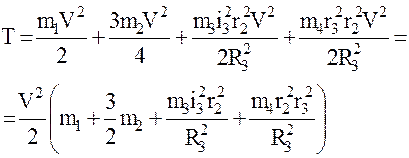 (1.8)
(1.8)
или
T= , (1.9)
, (1.9)
где mпр= =3,68 кг (1.10)
=3,68 кг (1.10)
Величину mпр=const будем называть приведенной массой. Найдем производную от кинетической энергии по времени
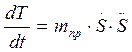 (1.11)
(1.11)
Теперь вычислим правую часть уравнения (1.1) - сумму мощностей внешних и внутренних сил.
Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения
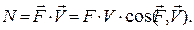 (1.12)
(1.12)
Рассматриваемая нами механическая система является неизменяемой, т. е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
 (1.13)
(1.13)
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы


Сумма мощностей остальных сил
 (1.14)
(1.14)
или, раскрывая скалярные произведения,
 (1.15)
(1.15)
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:

 |
В состоянии покоя приведенная сила равна нулю. Полагая
 , получаем условие равновесия системы
, получаем условие равновесия системы

тогда, учитывая, что сила вязкого сопротивления 
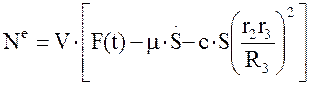 (1.16)
(1.16)
или
Ne=V Fпр , (1.17)
где
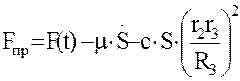 (1.18)
(1.18)
Величину Fпр будем называть приведенной силой.
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.18) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
 (1.19)
(1.19)
Запишем последнее уравнение в виде:
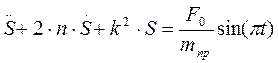 , (1.20)
, (1.20)
где введены коэффициенты, имеющие определенный физический смысл:
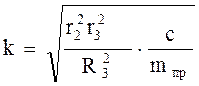 - циклическая частота свободных колебаний,
- циклическая частота свободных колебаний,
k = 3,06 с-1
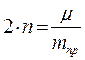 - показатель степени затухания колебаний.
- показатель степени затухания колебаний.
n = 0,14 с-1
Запишем начальные условия движения:
t=0 | 
 . (1.21)
. (1.21)
Выражения (1.20) и (1.21) совместно представляют математическую модель для решения второй задачи динамики.