Уравнение Максвелла в дифференциальной форме
Уравнения Максвелла применимы к поверхности любой величины и поэтому входящие в них величины относятся к разным точкам поля. Так, например, в уравнении:
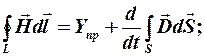
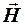 - напряженность магнитного поля в точках контура
- напряженность магнитного поля в точках контура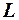 , Ограничивающего поверхность S, в то время как поток вектора
, Ограничивающего поверхность S, в то время как поток вектора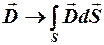 зависит от значения
зависит от значения в точках самой поверхности.
в точках самой поверхности.
Можно, однако, преобразовать эти уравнения в такую форму, чтобы все величины относились к одной и той же точке поля. Для этого уравнения Максвелла нужно применить к поверхности бесконечно малой величины.
Согласно теореме Стокса:
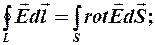
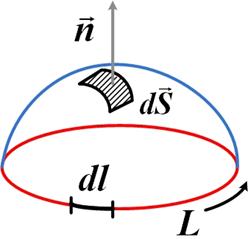
Тогда первое уравнение:
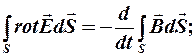
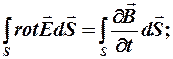
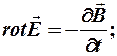 (I)
(I)
Справа интеграл зависит только от времени, → при фиксированном контуре правая часть никак не меняется при любых изменениях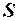 .
.
Символ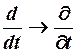 ;
;
Второе уравнение:
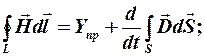
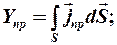
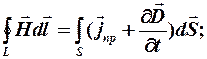
По теореме Стокса:
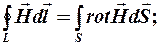
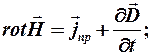 (II)
(II)
Расхождения электрической и магнитной индукции
Третье и четвертое уравнения Максвелла:
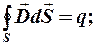
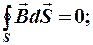
Переход от интегральной к дифференциальной форме согласно теореме Остроградского – Гаусса:
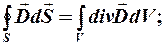
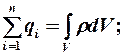
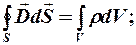
 (3)
(3)
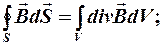

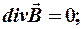 (4)
(4)
Схема уравнений Максвелла в дифференциальной форме:
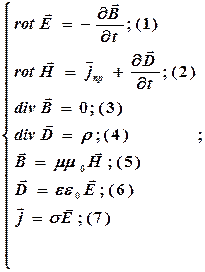
(σ - удельная проводимость)
Выводы. Значения теории Максвелла.
1.Уравнения Максвелла не выводятся.
2.Уравнения Максвелла позволяют определить основные характеристики поля (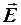 ,
, ,
,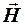 ,
,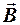 ) в каждой точке пространства в любой момент времени, если известны источники поля, плотность тока
) в каждой точке пространства в любой момент времени, если известны источники поля, плотность тока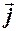 и плотность заряда
и плотность заряда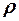 .
.
3.Сама по себе система уравнений Максвелла не имеет определенных решений, то есть совокупность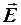 ;
; ;
;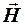 ;
;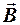 ;
;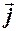 ;
;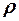 как конкретных функций координат и времени, существует только при наложении дополнительных условий, характеризующих тот или иной реальный объект.
как конкретных функций координат и времени, существует только при наложении дополнительных условий, характеризующих тот или иной реальный объект.