Раскраска графа. Хроматические полиномы. Алгоритм раскраски

Раскраска графа. Хроматические полиномы. Алгоритм раскраски.

Вершинная К раскраска графа-присвоения его вершинам К различных цветов. Никакие 2 не должны быть одного цвета.

-- правильная 3-раскраска

Хроматическое число Х(G) –минимальное число К, для которого G вершина К –раскрашиваемый Х(G)=К –граф –хроматический.

К - раскраска графа G=(V,E) порождает разбиения (V1, V2, V3, ) множества V, где каждое 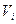-подмножество вершин, которым присвоен цвет i –независимо множества.

Теорема

Очевидно, что Х = () для полных графов и циклов нечётные длины. Для остальных графов Х Хроматические полиномы Две раскраски графа считаются различными, если хотя бы одной вершине присваиваются разные цвета.

Следствие

Если мы имеем полные графы : H1, Н2, Н3…. поэтому Р(G,)=Р(Н1, )+Р(Н2, )+….Р(,) Итак, хроматический полином – линейная комбинация хроматических полиномов…

Теорема

и const.=0 Все коэффициенты целые и чередуются ……. Пусть граф G с n вершинами и m рёбрами. е – ребро G .Тогда G- е -граф на n…

Теорема

Если наибольшая из степеней вершин графа G равна Р , то этот граф -раскрашиваемый.

Теорема Брукса

Пусть наибольшая из степеней вершин графа равна Р. Тогда G-P- раскрашиваемый, за исключением тех случаев ,когда

1) G содержит в качестве компонента граф 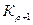или

2) Р=2 и цикл нечётной длинны является компонентой G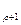

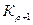- полный граф степени Р+1

Теорема

Любой планарный граф G – раскрашиваемый.

Теорема

Каждый планарный граф 5 раскрашиваемый.

Гипотеза 4-х красок

I. Всякий планарный граф, имеющий менее 52 вершин -4раскрашиваемый II. Любой, не содержащий треугольников планарный граф 3-раскрашиваемый III. Гипотеза 4-х красок верна для гамильтоновых планарных графов.

Теорема

Карта G -2-х – раскрашиваемая тогда и только тогда , когда G – эйлеров граф.

Теорема Визинга

Дан граф Многочлен имеет вид: (а, в, с –положительный const.)

Пример

+=+3+На некотором шаге выбираем 2 вершины U,Vn: