Соотношения между непрерывными и дискретными преобразованиями
Пара преобразований для обычного определения дискретного преобразования Фурье (ДПФ) N-точечной временной последовательности x[n] и соответствующей ей N-точечной последовательности преобразования Фурье X[k] дается выражениями
 , (18)
, (18)
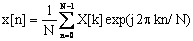 . (19)
. (19)
Чтобы по отсчетам данных получить спектральные оценки в соответствующих единицах измерения энергии или мощности, запишем дискретно-временной ряд Фурье (ДВРФ), который можно рассматривать как некоторую аппроксимацию непрерывно-временного преобразования Фурье (НВПФ), основанную на использовании конечного числа отсчетов данных:
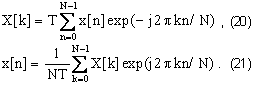
Для того, чтобы показать характер соответствия ДВРФ (дискретные функции и во временной и в частотной областях) и НВПФ (непрерывные функции во временной и в частотной областях), нам потребуется последовательность из четырех линейных коммутативных операций: взвешивания во временной и частотной областях и взятия отсчетов или дискретизации как во временной, так и в частотной областях. Если операция взвешивания выполняется в одной из этих областей, то, согласно теореме свертки, ей будет соответствовать выполнение операции фильтрации (свертки) в другой области с функцией sinc. Точно также, если в одной области выполняется дискретизация, то в другой выполняется операция периодического продолжения. Так как взвешивание и взятие отсчетов являются линейными и коммутативными операциями, то возможны различные способы их упорядочения, дающие одинаковый конечный результат при различных промежуточных результатах. На рис.2 показаны две возможные последовательности выполнения этих четырех операций.

Рис. 2. Две возможные последовательности из двух операций взвешивания и двух операций взятия отсчетов, связывающие НВПФ и ДВРФ: FW - применение окна в частотной области; TW - применение окна во временной области; FS - взятие отсчетов в частотной области; TS - взятие отсчетов во временной области.
1 - преобразование Фурье с непрерывным временем, уравнение (1);
4 - преобразование Фурье с дискретным временем, уравнение (22);
5 - ряд Фурье с непрерывным временем, уравнение (25);
8 - ряд Фурье с дискретным временем, уравнение (27)
В результате выполнения операций взвешивания и взятия отсчетов в узлах 1, 4, 5 и 8 будут иметь место четыре различных типа соотношений Фурье. Узлы, в которых функция в частотной области непрерывна, относятся к преобразованиям Фурье, а узлы, в которых функция в частотной области дискретна относятся к рядам Фурье (подробнее см. в [1]).
Так в узле 4 взвешивание в частотной и дискретизация во временной области порождает дискретно-временное преобразование Фурье (ДВПФ), которое характеризуется периодической функцией спектра в частотной области с периодом 1/T Гц:
 (22)
(22)
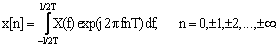 (23)
(23)
Заметим, что выражение (22) определяет некоторую периодическую функцию, совпадающую с заданной в узле 1 исходной преобразованной функцией только на интервале частот от -1/2T до 1/2T Гц. Выражение (22) связано с Z-преобра-зованием дискретной последовательности x[n] соотношением
 ( 24 )
( 24 )
Таким образом, ДВПФ - это просто Z-преобразование, вычисленное на единичной окружности и умноженное на T.
Если продвигаться от узла 1 к узлу 8 на рис.2 по нижней ветви, в узле 5 операции взвешивания во временной области (ограничения длительности сигнала) и дискретизации в частотной порождают непрерывно-временной ряд Фурье (НВРФ). Используя приведенные в таблицах 1 и 2 свойства и определения функций, получим следующую пару преобразований
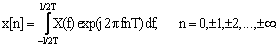 (25)
(25)
 (26)
(26)
Заметим, что выражение (26) определяет некоторую периодическую функцию, которая совпадает с исходной (в узле 1) только на интервале времени от 0 до NT.
Независимо от того, какая из двух последовательностей четырех операций выбрана, окончательный результат в узле 8 будет одним и тем же - дискретно-временным рядом Фурье, которому соответствует следующая пара преобразований, полученных с использованием свойств, указанных в таблице 1.
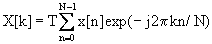 , (27)
, (27)
где k=-N/2, . . . ,N/2-1
 , (28)
, (28)
где n=0, . . . ,N-1 ,
Теорема о энергии для этого ДВРФ имеет вид:
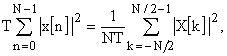 , (29)
, (29)
и характеризует энергию последовательности из N отсчетов данных. Обе последовательности x[n] и X[k] периодичны по модулю N, поэтому (28) можно записать в форме
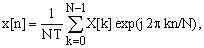 , (30)
, (30)
где 0  n
n  N. Множитель T в (27) - (30) необходим для того, чтобы (27) и (28) являлись в действительности аппроксимацией интегрального преобразования в области интегрирования
N. Множитель T в (27) - (30) необходим для того, чтобы (27) и (28) являлись в действительности аппроксимацией интегрального преобразования в области интегрирования
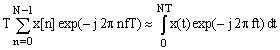 .(31)
.(31)