ARCH – ПРОЦЕССЫ

(авторегрессионые условно гетероскедастичные)

 

Из теории прогнозирования известно, что прогнозы с минимальной ошибкой обеспечивают условное математическое ожидание, базирующееся на знании всей предшествующей информации.

Часто, в особенности в финансовых моделях, нужно уметь предсказывать не только тенденцию показателя и его периодические колебания (или любые другие систематические изменения, улавливаемые ARMA-моделями), но и дисперсию.

В традиционных эконометрических моделях дисперсия предполагается постоянной. Даже небольшой опыт работы с временными рядами свидетельствует о том, что требование гомоскедастичности трудновыполнимо и малореально.

Более того, даже если безусловная дисперсия ошибок постоянна, условная дисперсия, которая зависит от прошлой информации, может быть подвержена случайным колебаниям.

Для того, чтобы лучше прочувствовать разницу между условной и безусловной дисперсиями, обратимся к простому примеру:

Пусть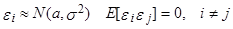

Безусловное долгосрочное (long-run) математическое ожидание равно:

Условное математическое ожидание X, базирующиеся на том, что 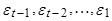известны, рассчитывается иначе. Обозначим через всю информацию, известную до момента (t-1) включительно. Тогда

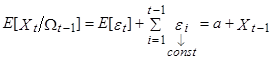
Безусловная дисперсия :

(дисперсия суммы независимых случайных величин равна сумме дисперсий)

Условная дисперсия:

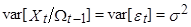
Т.к. дисперсия const=0 (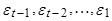известны, т.е. константы).

Из этого примера видно, во-первых, что условная и безусловная дисперсии различны, и во-вторых, что прогноз условной дисперсии предпочтительнее (она меньше).

Теперь допустим, что условная дисперсия непостоянна. Что же делать, если дисперсия остатков в эконометрических моделях меняется со временем, и в этом измерении нет определенных закономерностей?

Один из простых способов – ввести независимую переменную, которая поможет предсказать дисперсию.

Рассмотрим простейший случай:

,

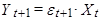где - исследуемая переменная,

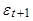- белый шум с дисперсией ,

- независимая переменная, наблюдаемая до момента t.

Если , то последовательность - известный процесс белого шума с постоянной дисперсией.

Однако когда элементы последовательности не равны между собой, дисперсия зависит от фактического значения .

Константа выносится за знак дисперсии в квадрате.

Итак, введение последовательности может обьяснить изменение последовательности .

Как предварительный шаг к методологии, которую мы будем рассматривать, еще на одном примере покажем, что условные прогнозы предпочтительнее безусловных прогнозов.

Рассмотрим стандартную модель ARMA(1,0):

,

по которой нужно предсказать .

Условный прогноз есть:

(известно)

Если для прогноза используется условное математическое ожидание, то прогнозируемая дисперсия ошибки будет равна:

Если же используется безусловный прогноз, то это долгосрочное (long-run) среднее значение последовательности , которое всегда равно:

Безусловный прогноз дисперсии ошибки равен тогда:

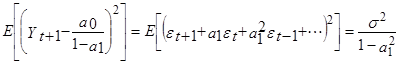
С этим результатом мы знакомы:

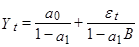
AR(1) для центрированных значений можно представить как бесконечный процесс МА.

Если (а это для всех справедливо: 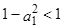), т.е. для стационарных процессов 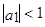, то безусловный прогноз имеет большую дисперсию, чем условный прогноз. Таким образом, условные прогнозы (если они берут в расчет известные текущие и прошлые значения рядов) предпочтительнее.

На практике эту модель модифицируют введением коэффициентов и оцениванием уравнения в логарифмической форме.

,

где

Логарифмическое преобразование дает линейное уравнение регрессии, которое легко оценивается (методом наименьших квадратов).

Основная сложность такой стратегии – в том, что она предполагает наличие специфического источника для измерения дисперсии, а для такого выбора не оказывается серьезных оснований.

Вместо специфического поиска и (или) трансформации данных Энгл (Engle) в 1982 году показал возможность одновременного моделирования среднего значения и дисперсии рядов. Стратегия весьма проста.

Энгл предложил моделировать условную дисперсию ошибки как процесс AR(p), используя квадраты оцениваемых остатков:

(1)

, где - белый шум.

(2)