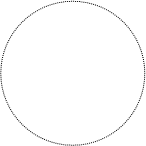
Векторная диаграмма колебания с УМ

Из аналитического выражения колебания с УМ (3.8) видно, что его амплитуда U₀ сохраняется неизменной, следовательно, вектор комплексной амплитуды 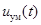не изменяет свою длину и может только вращаться на комплексной

плоскости (рис. 3.35). Годограф этого вектора представляет

собой окружность.

Аналитическое выражение простого колебания с УМ имеет следующий вид

,

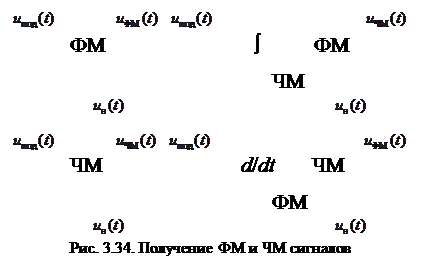
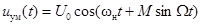где М – максимальное отклонение фазы от среднего значения называют индексом модуляции.

Изменение мгновенной частоты простого колебания с УМ происходит по закону

,

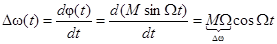где 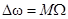(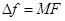) – девиация частоты.

Спектр простого колебания с УМ

Для определения спектра простого колебания с УМ удобно перейти к его комплексному сигналу

(3.9)

Из теории функций Бесселя известно, что

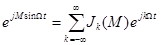, (3.10)

где J_k(M) – функции Бесселя первого рода порядка k от аргумента М (k = 0, ±1, ±2,…). Они обладают свойством

.

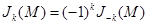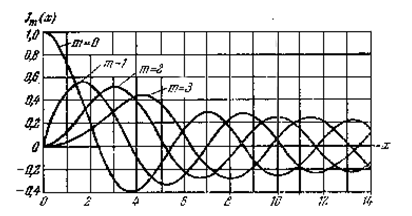Графики функций Бесселя приведены на рис. 3.36.

Рис. 3.36. Графики функций Бесселя

Подставляя (3.10) в (3.9), получаем

.

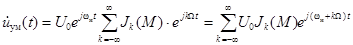Вернёмся к действительному сигналу

.

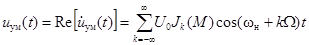Спектр простого сигнала с УМ, соответствующий полученному выражению, приведён на рис. 3.37.

 

Для определения ширины спектра простого сигнала с УМ учтём ещё одно свойство функций Бесселя – с ростом их порядка увеличивается начальная область значений аргумента М, при которых модуль этих функций очень мал. Обычно, пренебрегают боковыми компонентами с номерами k > M+1, считая практическую ширину спектра

.

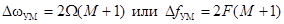Таким образом, при М >> 1

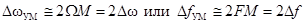
и можно считать, что ширина спектра простого колебания с УМ вдвое больше его девиации частоты и существенно больше (в М раз) ширины спектра АМ сигнала.

При М << 1 достаточно в спектре этого колебания удержать первую пару боковых и считать его ширину

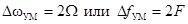
равной ширине спектра простого АМ сигнала.