Моделирование случайных величин с дискретными распределениями
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА № 43
Отчет защищен:
Преподаватель:
| Гурнов К. Б. | ||||
| должность, уч. степень, звание | подпись, дата | инициалы, фамилия |
| Отчет по лабораторной работе № 1 |
| «Моделирование случайных величин с дискретными распределениями». |
| по дисциплине: Компьютерное моделирование сложных систем |
| Вариант 12 |
РАБОТУ ВЫПОЛНИЛА:
| Студентка | Иванина Е.В. | ||||
| подпись, дата | инициалы, фамилия |
Санкт-Петербург
2009
Цель работы: Изучение способов воспроизведения на ЭВМ случайных данных с дискретными законами распределения и определения их статистических характеристик.
Задание:
Биноминальное распределение m=20, k=1,2..20, p=0.8
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Согласно заданию преподавателя, в котором определяются моделируемое распределение и его параметры, сформировать случайные данные в виде вектора. Провести ранжирование сформированной выборки, построить дискретный вариационный ряд и графически представить его в виде полигона. Сравнить полученный результат моделирования с соответствующим законом распределения.
- Построить кумулятивную кривую как зависимость относительной накопленной частоты wk от k, сравнить её с соответствующей функцией распределения.
- Повторить действия, описанные в п.1 и п.2, не менее четырёх раз при различных (увеличивающихся) объёмах выборки с целью иллюстрации выполнения теоремы Гливенко-Кантелли о сходимости по вероятности эмпирической и теоретической функций распределения.
- Построить графики зависимостей выборочного среднего (либо другой выборочной характеристики) от одного из параметров заданного распределения при трёх-четырёх различных объёмах выборки с целью иллюстрации выполнения закона больших чисел в форме Хинчина.
- Используя описанные выше способы получения последовательности из n независимых испытаний по схеме Бернулли, проиллюстрировать выполнение интегральной теоремы Муавра-Лапласа. Для этого необходимо сформировать M выборок объёма n, по каждой из которых вычислять нормированную величину ζ=(v1-np)/√np(1-p) (v1 – частота единичного значения). Показать, что при увеличении М относительная частота попадания величины ζ в интервал [a, b] стремится к разности Φ(b)-Φ(a), где Φ(…) – интеграл вероятностей, его расчёт в Mathcad осуществляется функцией cnorm(…).
ВЫПОЛНЕНИЕ РАБОТЫ
1.

|
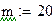
|

|

|
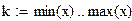
|
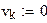
|
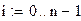
|

|

|
Размер выборки
Количество испытаний в схеме Бернулли
Вероятность успеха в одиночном испытании
Получаем выборку с параметрами m и p
Ранжируем выборку
Получаем вариационный ряд
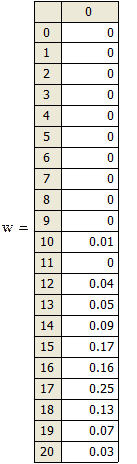
Получаем относительные частоты каждой случайной
величины

|
|

|

|
|
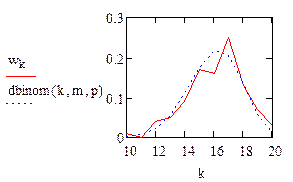
Полигон и закон распределения
wk - на графике отображает распределение нашей полученной случайной величины
dbinom(k, m, p)- на графике отображает распределение Бернулли
2.

|

|
Относительно накопленные частоты
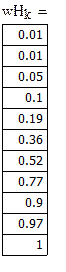
|
|
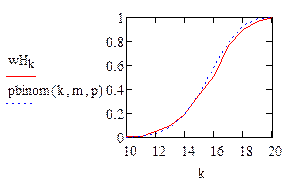
Кумулятивная кривая и функция распределения
pbinom(k, m, p) на графике отражает функцию распределения нашей полученной случайной случайно величины
wHk на графике отображает функцию распределения по Бернулли
3.
Повторим действия, описанные в п.1 и п.2 не менее четырёх раз при увеличивающихся объёмах выборки

|
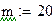
|

|

|
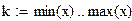
|
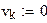
|
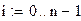
|

|

|
Размер выборки
Количество испытаний в схеме Бернулли
Вероятность успеха в одиночном испытании
Получаем выборку с параметрами m и p
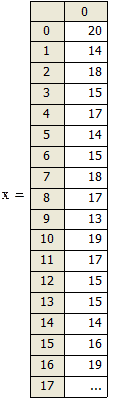
Ранжируем выборку
Получаем вариационный ряд
Получаем относительные частоты каждой случайной
величины

|

|

|
|

|
Полигон и закон распределения
wk - на графике отображает распределение нашей полученной случайной величины
dbinom(k, m, p)- на графике отображает распределение Бернулли

|

|

|
Относительно накопленные частоты

|
Кумулятивная кривая и функция распределения
pbinom(k, m, p) на графике отражает функцию распределения нашей полученной случайной случайно величины
wHk на графике отображает функцию распределения по Бернулли

|
|

|

|
|
|
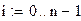
|
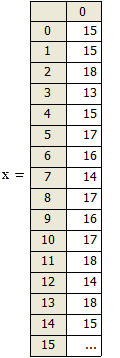
Размер выборки
Количество испытаний в схеме Бернулли
Вероятность успеха в одиночном испытании
Получаем выборку с параметрами m и p
Ранжируем выборку

|
Получаем вариационный ряд

|
Получаем относительные частоты каждой случайной
величины
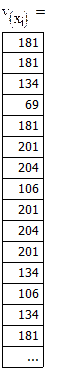
|

|
|

|

|
Полигон и закон распределения
wk - на графике отображает распределение нашей полученной случайной величины
dbinom(k, m, p)- на графике отображает распределение Бернулли

|

|
Относительно накопленные частоты

|

|
Кумулятивная кривая и функция распределения
pbinom(k, m, p) на графике отражает функцию распределения нашей полученной случайной случайно величины
wHk на графике отображает функцию распределения по Бернулли
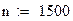
|
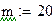
|

|

|
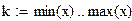
|
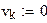
|
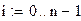
|

|

|
Размер выборки
Количество испытаний в схеме Бернулли
Вероятность успеха в одиночном испытании
Получаем выборку с параметрами m и p
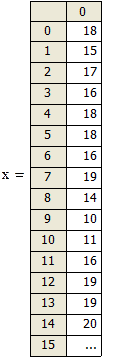
Ранжируем выборку
Получаем вариационный ряд
Получаем относительные частоты каждой случайной
величины

|

|
|
|

|
Полигон и закон распределения
wk - на графике отображает распределение нашей полученной случайной величины
dbinom(k, m, p)- на графике отображает распределение Бернулли

|

|

|
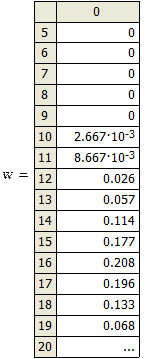
Относительно накопленные частоты
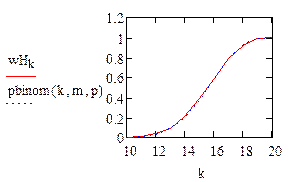
|
Кумулятивная кривая и функция распределения
pbinom(k, m, p) на графике отражает функцию распределения нашей полученной случайной случайно величины
wHk на графике отображает функцию распределения по Бернулли
4.

|
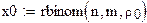
|
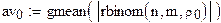
|

|

|

|
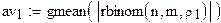
|
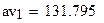
|
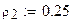
|
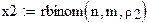
|
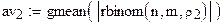
|

|

|
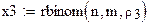
|

|

|
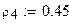
|
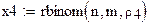
|
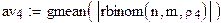
|

|

|
задаем вероятность
формируем выборку с параметрами n, m, po
вычисление выборочного геометрического
среднего
задаем вероятность
формируем выборку с параметрами n, m, po
вычисление выборочного геометрического
среднего
задаем вероятность
формируем выборку с параметрами n, m, po
вычисление выборочного геометрического
среднего
задаем вероятность
формируем выборку с параметрами n, m, po
вычисление выборочного геометрического
среднего
задаем вероятность
формируем выборку с параметрами n, m, po
вычисление выборочного геометрического
среднего
Зависимость геометрического среднего от вероятностей
5. Выполнение интегральной теоремы Муавра-Лапласа по схеме Бернулли

|
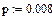
|
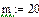
|
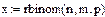
|
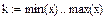
|
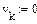
|
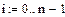
|
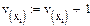
|
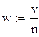
|
Объем выборки
Вероятность успеха в одиночном испытании
Количество испытаний в схеме Бернулли
Получаем выборку с параметрами m и p
Ранжируем выборку
Получаем вариационный ряд
Получаем относительные частоты каждой случайной
величины
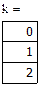
|

|
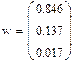
|

|

|
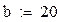
|

|
Вычисляем нормированную величину ζ
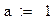
|
[a, b] – интервал
Φ(…) – интеграл вероятностей
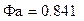
|
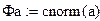
|
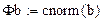
|

|
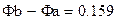
|
Относительная частота попаданий величины ζ в интервал [a, b] стремится к этой разности


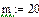
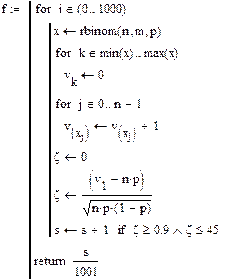
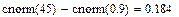
|
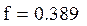
Вывод по работе:В ходе выполнения данной лабораторной работы я изучила способы воспроизведения на ЭВМ случайных данных с дискретными законами распределения и определения их статистических характеристик.
- Был изучен более подробно закон распределения Бернулли;
- Проиллюстрировано выполнение теоремы Гливенко-Кантелли;
- Проиллюстрировано выполнение закона больших чисел в форме Хинчина;
- Проиллюстрировано выполнение интегральной теоремы Муавра-Лапласса.