Сложение угловых моментов

1. Понятие углового момента можно распространить и на системы частиц. Для этого рассмотрим простейшую изолированную систему из двух невзаимодействующих микрочастиц: 1 и 2.

Оператором углового момента системы частиц 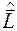называют сумму операторов угловых моментов ее частей и :

.

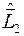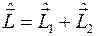Так же определяется и оператор проекции углового момента на избранное направление. Например,

.

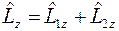Состояние первой микрочастицы определяется волновой функцией 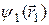, зависящей только от координат первой микрочастицы. Она должна быть собственной функцией операторов 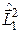и 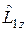. Точно так же 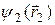является собственной функцией операторов 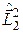и 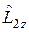. Состояние системы невзаимодействующих микрочастиц описывается волновой функцией

.

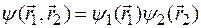При этом условие нормировки волновой функции системы будет выполнено автоматически

.

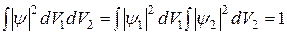Заметим, что операторы и 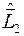коммутируют. Действительно, каждый из операторов действует только на динамические переменные своей частицы. Поэтому

.

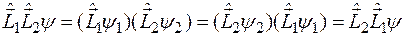При отсутствии внешнего воздействия в такой системе будут сохраняться моменты импульса каждой частицы и момент импульса системы. поэтому оператор

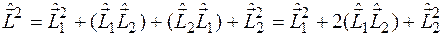
будет иметь собственные значения 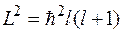, где 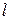-квантовое число результирующего момента системы. При этом собственные значения операторов 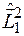, 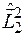равны , .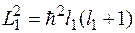

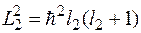Так как

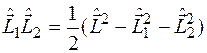
и оператор в правой части имеет собственные значения, то и оператор в левой части так же должен иметь собственные значения

.

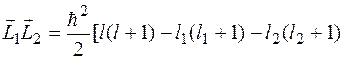Из равенств 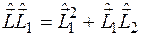и следует

,

.

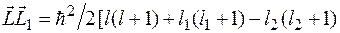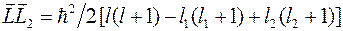Это значит, что углы между направлениями угловых моментов 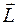, и принимают дискретный ряд значений.

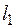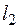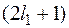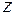При заданных значениях и каждый из моментов и может иметь и проекций на ось , соответственно. Поэтому при заданных значениях 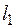и 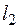получается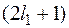 различных состояний. Волновые функции этих состояний обозначают .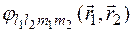

Из этих базисных состояний можно построить волновую функцию любого состояния с заданными значениям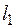и и .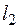

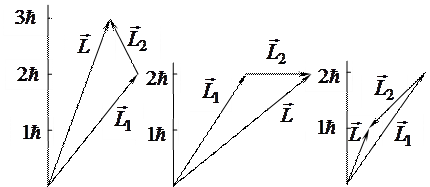
Полученные результаты принято изображать на векторных диаграммах. Векторы 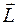, и изображаются стрелками длиной 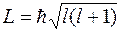, , 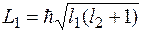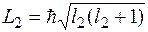. Они располагаются в пространстве так, чтобы проекции на ось 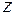имели значения , , 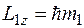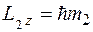. Причем . Его максимальное значение равно 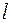и равно сумме максимальных значений 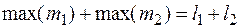, т.е.

.

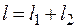Линейно-независимые состояния, из которых может быть составлено любое состояние с заданными значениям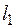и и 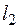может выбрать и иначе. Поскольку при заданных 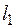и 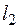полный угловой момент и его проекция имеют определенные значения, определяемые квантовыми числами 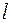и , то можно ввести волновые функции 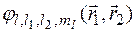. Их число так же должно быть равно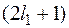 . Они так же образуют базисный набор функций. 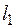Из них так же линейной комбинацией можно составить волновую функцию любого состояния с заданными значениями и .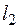

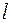При различных ориентациях угловых моментов и квантовое число принимает ряд значений (при )

,

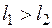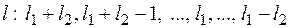Всего значений, и при каждом из них получается проекция .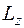

Полное количество различных состояний равно

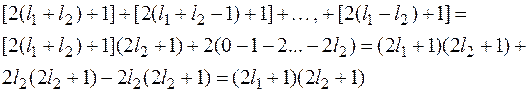
Если частицы не взаимодействуют, и нет внешних сил, то сохраняется не только результирующий момент, но и моменты и . При наличии взаимодействия моменты и в отдельности не сохраняются, а сохраняется только результирующий момент системы. Если взаимодействие слабое, то по аналогии с классической механикой длины векторови при этом практически изменяться не будут. На векторной диаграмме эти векторы будут прецессировать вокруг вектора 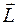с одной и той же угловой скоростью. К такому приводит и последовательное квантовое рассмотрение.