Приближенная количественная теория атома гелия
Задача о движении двух электронов в поле ядра аналогична задаче о движении двух планет в гравитационном поле Солнца. В небесной механике разработаны достаточно точные приближенные методы расчета движения планет. В их основе лежит теория возмущений, использующая тот факт, что взаимодействие между планетами мало по сравнению с взаимодействием каждой планеты с Солнцем.
В нулевом приближении взаимодействием между планетами можно совсем пренебречь. Используя решение, полученное в нулевом приближении, можно затем учесть взаимодействие между планетами в первом приближении, после этого найти второе приближение и т.д.
Таким же методом решается задача и в квантовой механике. В нулевом приближении не учитывается взаимодействие электронов друг с другом. Но в квантовой механике энергия взаимодействия электронов друг с другом все-таки не мала, а сравнима с энергией взаимодействия каждого электрона ядром. Однако получающиеся результаты довольно удовлетворительны, чем и оправдывается использование методов теории возмущений.
Итак, для решения уравнения Шредингера
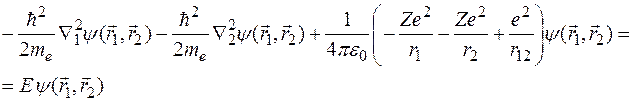
в нулевом приближении энергию взаимодействия электронов друг с другом
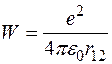
учитывать не будем.
Оставшийся Гамильтониан представим в виде
 ,
,
где
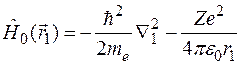 ,
, 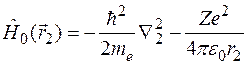 .
.
Каждый из этих операторов имеет собственные функции 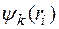 и собственные значения
и собственные значения 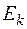 .
.
Таким образом, в нулевом приближении уравнении Шредингера принимает вид
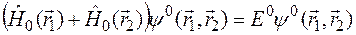 .
.
Его собственными значениями будет сумма собственных значений энергии электронов в кулоновском поле ядра
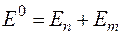 ,
,
а собственными функциями будут функции, равные произведению волновых функций электронов в одноэлектронных ионах
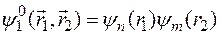 ,
, 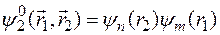 .
.
Сами по себе эти функции не являются ни симметричными ни асимметричными, но из них можно построить линейную комбинацию
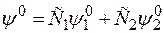 .
.
При 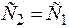 получается симметричная координатная функция
получается симметричная координатная функция
 ,
,
при 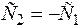 - антисимметричная
- антисимметричная
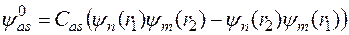 .
.
Нормировочные постоянные равны 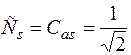 .
.
Отметим, что в нулевом приближении собственные значения энергии пара- и ортогелия совпадают.
Представим теперь энергию возмущения 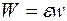 , где
, где  - некоторый малый параметр. Тогда волновую функцию и энергию произвольного состояния можно представить в виде разложения по малому параметру
- некоторый малый параметр. Тогда волновую функцию и энергию произвольного состояния можно представить в виде разложения по малому параметру
 ,
,
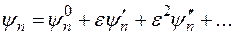 .
.
Подставим эти разложения в исходное уравнение Шредингера
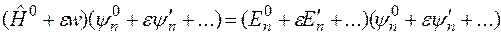 .
.
Оставляя в этом уравнении слагаемые первого порядка малости получим
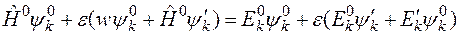 .
.
Так как 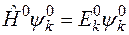 , то получаем уравнение
, то получаем уравнение
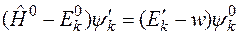 .
.
Это неоднородное уравнение для определения 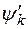 с неопределенным параметром
с неопределенным параметром 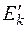 .
.
Чтобы это уравнение имело непрерывные решения необходимо, чтобы его правая часть была ортогональна к решению однородного уравнения
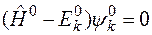 ,
,
т.е. к 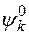 . Это значит, что
. Это значит, что
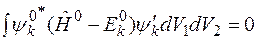 .
.
Умножим неоднородное уравнение на 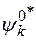 и проинтегрируем по всем переменным
и проинтегрируем по всем переменным
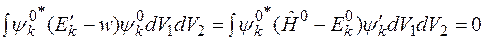 .
.
Отсюда следует
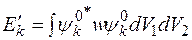 .
.
Следовательно, поправка первого порядка к энергии невозмущенного состояния в атоме гелия вычисляется по формуле
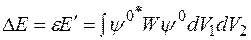 .
.
Подставляя сюда волновые функции нулевого порядка, получим
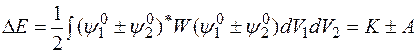 ,
,
где введены обозначения
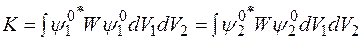 ,
,
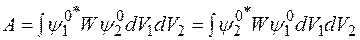 .
.
Верхний знак относится к симметричным координатным функциям (антипараллельной ориентации спинов), нижний знак относится к антисимметричным координатным функциям (параллельной ориентации спинов).
Таким образом, для парагелия энергия состояний вычисляется по формуле
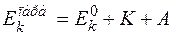 ,
,
для ортогелия
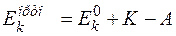 .
.