Анализ АВС
Управление в логистике характеризуется, как правило, большой номенклатурой управляемых объектов: широкий ассортимент товаров, большое число покупателей или поставщиков, разнообразные грузы и т. п. В процессе работы с каждым отдельным объектом, например, позицией ассортимента, предприниматель получает какую-то часть общего результата. При этом с точки зрения вклада в общий результат управляемые объекты далеко не равноценны.
Идея метода АВС состоит в том, чтобы из всего множества объектов выделить наиболее значимые. Таких объектов, как правило, немного, и именно на них необходимо сосредоточить основное внимание.
В экономике широко известно так называемое правило Парето (20/80), согласно которому лишь пятая часть (20 %) от всего количества объектов, с которыми обычно приходится иметь дело, дает примерно 80 % общего результата. Вклад остальных 80 % объектов составляет только 20 % общего результата.
Суть принципа Парето состоит в том, что в процессе управления нерационально уделять объектам, образующим малую часть вклада, такое же внимание, как и объектам первостепенной важности.
Согласно методу Парето множество управляемых объектов делится на две неодинаковые части. Широко применяемый в логистике метод АВС предлагает разделение на три части (группа А, группа В, группа С). При этом предварительно все управляемые объекты необходимо оценить по степени вклада в результат деятельности.
Рассмотрим следующий пример. В табл. 1 перечислены 20 объектов, вклад каждого из которых в общий результат оценен в условных единицах и приведен в графе 2. В итоговой строке графы 2 приведен общий результат деятельности. В графе 3 указана доля каждого из объектов в общем результате, выраженная в процентах.
Расположим в табл. 2 объекты в порядке убывания доли вклада. Как видим, первые 2 позиции (10 % объектов) списка, упорядоченного подобным образом, дали 75 % результата. Следующие 5 позиций (25 % объектов) – дали 20 % общего результата, и, наконец, оставшиеся 13 позиций (65 % объектов) дали всего лишь 5 % общего результата.
Предположим, что первоначально расходы на управление распределялись между всеми объектами равномерно вне зависимости от вклада объекта в конечный результат, при этом стоимость управления одним объектом составляла 5 условных единиц. Общая стоимость управления составляла 100 условных единиц (20 * 5).
Увеличим в 2 раза стоимость управления объектами группы А и снизим в 2 раза стоимость управления объектами группы С. Стоимость управления объектами группы В оставим без изменения.
Тогда общая стоимость управления составит
2 * 10 + 5 * 5 + 13 * 2,5 = 77,5 ,
т. е. сократится на 22,5 условных единиц.
Ухудшение управления группой С скорее всего не окажет значимого влияния на общий результат в связи с незначительной ролью этой группы. В то же время улучшение управления группой А может этот результат существенно улучшить.
Таким образом, перераспределение средств на управление, выполненное в соответствии с результатами анализа АВС, даст снижение затрат на управление и одновременно повысит его эффективность.
Т а б л и ц а 1. Оценка вклада объектов в общий результат
| № объекта | Вклад объекта, усл. ед. | Доля вклада объекта, % |
| 0,1 | ||
| 2,0 | ||
| 0,3 | ||
| 52,0 | ||
| 0,3 | ||
| 0,9 | ||
| 0,1 | ||
| Продолжение табл. 1 | ||
| № объекта | Вклад объекта, усл. ед. | Доля вклада объекта, % |
| 1,0 | ||
| 8,0 | ||
| 3,0 | ||
| 0,1 | ||
| 0,2 | ||
| 23,0 | ||
| 3,0 | ||
| 0,4 | ||
| 0,7 | ||
| 0,5 | ||
| 0,2 | ||
| 4,0 | ||
| 0,2 | ||
| Итого | 10 000 |
Т а б л и ц а 2. Разделение объектов на группы А, В и С
| № объекта | Вклад объекта, усл.ед. | Доля вклада объекта, % | Вклад нарастающим итогом, % | Группа и ее вклад в результат |
| 52,0 | 52,0 | Группа А | ||
| 23,0 | 75,0 | 75 % | ||
| 8,0 | 83,0 | |||
| 4,0 | 87,0 | Группа В | ||
| 3,0 | 90,0 | 20 % | ||
| 3,0 | 93,0 | |||
| 2,0 | 95,0 | |||
| 1,0 | 96,0 | |||
| 0,9 | 96,9 | |||
| 0,7 | 97,6 | |||
| 0,5 | 98,1 | |||
| 0,4 | 98,5 | |||
| 0,3 | 98,8 | |||
| 0,3 | 99,1 | Группа С | ||
| 0,2 | 99,3 | 5 % | ||
| 0,2 | 99,5 | |||
| 0,2 | 99,7 | |||
| 0,1 | 99,8 | |||
| 0,1 | 99,9 | |||
| 0,1 | 100,0 |
Графически метод АВС представлен на рис. 2. При построении кривой по оси ОХ откладывают объекты управления в порядке убывания значимости их вклада в конечный результат. По оси OY откладывают вклад каждого объекта в конечный результат нарастающим итогом, выраженный в процентах.
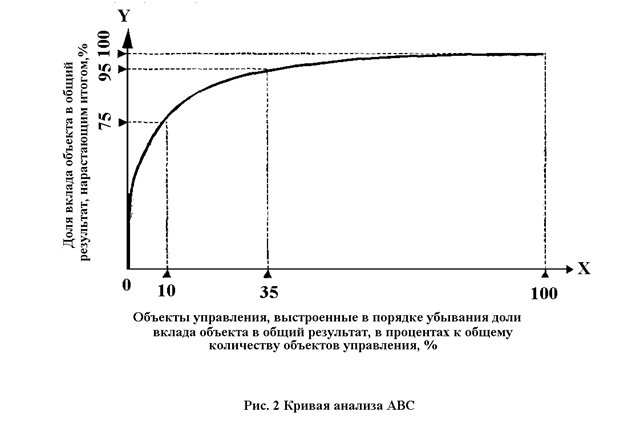
Недостатком метода АВС является отсутствие четкого критерия разделения на группы.
Поэтому важнейшей задачей совершенствования метода АВС является систематизация различных подходов, проведение сравнительных расчетов и сопоставление их результатов с целью выбора наилучшего варианта.
Анализ литературных источников показал, что существующие методы проведения анализа АВС могут быть разделены на три группы: эмпирический, дифференциальный и аналитический.
Эмпирический метод базируется на гипотезе, что деление на группы можно выполнять по аналогии, и поэтому границы групп выбираются по результатам проведенных ранее исследований. Использование эмпирического метода предусматривает выполнение следующих операций:
Полученные значения показателей Cj ранжируются – располагаются в убывающей последовательности

Затем производится присвоение новых индексов 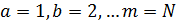 , где
, где  - общее количество наименований деталей номенклатуры, т. е.
- общее количество наименований деталей номенклатуры, т. е.
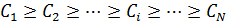
Для удобства расчетов вводятся относительные величины рассматриваемых показателей qj (в процентах)
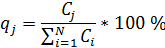
Величины 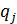 суммируются нарастающим итогом
суммируются нарастающим итогом
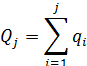
Интегральная (кумулятивная) зависимость 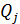 представляется в табличной форме в виде пар значений
представляется в табличной форме в виде пар значений 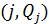 и затем может быть использована для подбора аналитической зависимости
и затем может быть использована для подбора аналитической зависимости 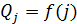 или представлена в виде графика (ось ординат Y – значение
или представлена в виде графика (ось ординат Y – значение 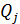 , ось абсцисс X – значение
, ось абсцисс X – значение  ).
).
По существу, эмпирический метод предусматривает выбор координат YA и YA+B, например, YA=75 %, YA+B =95 %.
Затем с помощью интегральной зависимости 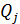 находятся значения XA и XA+B, позволяющие разделить позиции номенклатуры на группы А, В и С.
находятся значения XA и XA+B, позволяющие разделить позиции номенклатуры на группы А, В и С.
Дифференциальный метод может быть использован как для ранжированных показателей Cj , так и для исходных. В основу метода положены соотношения, опирающиеся на среднее значение показателя

В общем случае граничные значения для выделения групп рассчитываются с помощью коэффициентов, величины которых задаются. Например, к группе А должны быть отнесены позиции номенклатуры, показатели которых
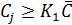 ,
,
а к группе В соответственно

Аналогично к группе С относим позиции номенклатуры, для которых
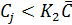
Несомненное достоинство дифференциального метода – простота. Нет необходимости ранжировать показатели и строить интегральную зависимость. Недостаток дифференциального метода – неопределенность выбора коэффициентов 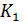 и
и  .
.
Аналитический метод. Особенность данного метода состоит в том, что деление на группы А, В и С производится на основе интегральной кривой 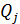 . Можно выделить два основных варианта этого метода – графический и аналитический.
. Можно выделить два основных варианта этого метода – графический и аналитический.
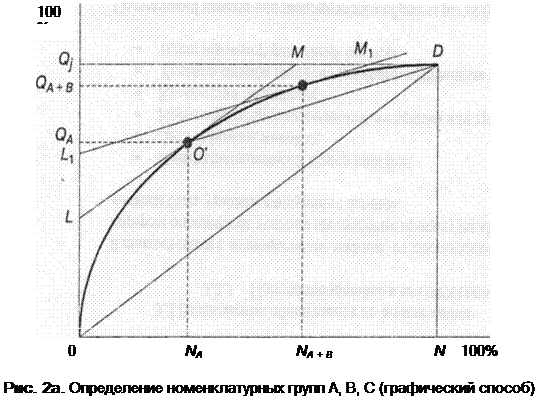
При графическом способе (рис. 2а) по оси ординат откладываются значения 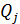 , по оси абсцисс – индексы 1,2,…,
, по оси абсцисс – индексы 1,2,…, , соответствующие присвоенным номерам позиции номенклатуры. Точки с координатами
, соответствующие присвоенным номерам позиции номенклатуры. Точки с координатами 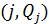 на графике соединяются плавной кривой
на графике соединяются плавной кривой 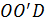 , которая всегда является выпуклой вверх. Затем проводится касательная LM к интегральной кривой
, которая всегда является выпуклой вверх. Затем проводится касательная LM к интегральной кривой 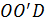 параллельно прямой OD. Прямая OD соответствует равномерному распределению показателя для всей номенклатуры
параллельно прямой OD. Прямая OD соответствует равномерному распределению показателя для всей номенклатуры
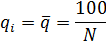
Абсцисса точки касания  (NA) отделяет от всей номенклатуры первую группу (группу А), в которую входят позиции номенклатуры с показателями
(NA) отделяет от всей номенклатуры первую группу (группу А), в которую входят позиции номенклатуры с показателями
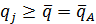 . Таким образом, к группе А относятся все позиции номенклатуры, у которых значения показателей
. Таким образом, к группе А относятся все позиции номенклатуры, у которых значения показателей 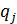 больше или равны среднему значению показателя для всей номенклатуры.
больше или равны среднему значению показателя для всей номенклатуры.
Соответственно ордината точки  (QA) указывает долю деталей группы А в процентах.
(QA) указывает долю деталей группы А в процентах.
Продолжим деление на группы оставшейся номенклатуры, воспользовавшись вышеописанным приемом. Соединим точку  с точкой D и проведем касательную к кривой
с точкой D и проведем касательную к кривой 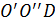 , параллельную прямой
, параллельную прямой 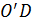 . Абсцисса точки касания
. Абсцисса точки касания 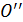 делит оставшуюся номенклатуру на группу В и группу С.
делит оставшуюся номенклатуру на группу В и группу С.
Для оставшейся номенклатуры величина среднего показателя составит
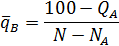
где  - число позиций, вошедших в группу А.
- число позиций, вошедших в группу А.
Таким образом, в группу В попадают позиции номенклатуры с показателями 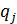 , удовлетворяющими неравенству
, удовлетворяющими неравенству

При аналитическом способе последовательность этапов определения номенклатурных групп следующая.
1. Позиции номенклатуры нормируются в интервале (0;1) и вводится аргумент х.
2. Выбирается аналитическая зависимость 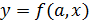 для аппроксимации интегральной кривой
для аппроксимации интегральной кривой 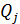 .
.
3. Определяются коэффициенты  с использованием метода наименьших квадратов.
с использованием метода наименьших квадратов.
4. В качестве критерия деления на группы выберем условие, что в группу А попадут все позиции номенклатуры, показатели которых 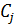 больше или равны среднему значению показателя для всей номенклатуры
больше или равны среднему значению показателя для всей номенклатуры 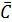 . Согласно теореме Лагранжа, на выпуклой кривой
. Согласно теореме Лагранжа, на выпуклой кривой 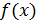 существует одна точка А, касательная в которой параллельна линии, соединяющей начало координат (0;0) и точку (1;1).
существует одна точка А, касательная в которой параллельна линии, соединяющей начало координат (0;0) и точку (1;1).
Для определения абсциссы точки А воспользуемся формулой
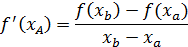
где  - производная функции
- производная функции 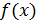 в точке касания А;
в точке касания А;
 - искомая абсцисса точки касания;
- искомая абсцисса точки касания;
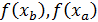 - значения функции в начальной
- значения функции в начальной  и конечной
и конечной 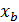 точках.
точках.
С учетом начальных условий уравнение запишется в виде
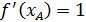
Решая это уравнение, находим  , затем ординату
, затем ординату  и количество позиций номенклатуры, относящихся к группе А
и количество позиций номенклатуры, относящихся к группе А
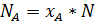
5. Для определения точки В введем новую систему координат, принимая за начало отсчета абсциссу  и ординату
и ординату  . С учетом, что конечная точка имеет координаты
. С учетом, что конечная точка имеет координаты 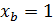 ,
,  , уравнение запишется в виде
, уравнение запишется в виде

Дальнейшие вычисления аналогичны п. 4: находим 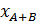 , затем
, затем  и
и