рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Полиграфия
- /
- Технологии и дизайна
Реферат Курсовая Конспект
Технологии и дизайна
Технологии и дизайна - раздел Полиграфия, Министерство Образования И Науки Российской Федерации ...
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный университет
технологии и дизайна»
Кафедра экономики и финансов
ЛОГИСТИКА
Методические указания к изучению дисциплины, выполнению
контрольных заданий, проведению практических занятий у студентов специальностей
080111.65 «Маркетинг»,
080502 «Экономика и управление на предприятии»,
080401.65 «Товароведение и экспертиза товаров»,
направлений
080100.62 «Экономика»,
080500.62 «Менеджмент»
заочной, очно-заочной, очной форм обучения
Составители
А. И. Богданов
А. В. Кураков
Санкт-Петербург
УТВЕРЖДЕНО
на заседании кафедры
25 марта 2010 г.,
протокол № 6
Рецензент
А. П. Селин
Подписано в печать 29 марта 2010 г. Формат 60 х 84 1/16
Усл. печ. л. 2,7. Тираж
Заказ № 60/10
Отпечатано в типографии СПГУТД
191028, Санкт-Петербург, ул. Моховая , 26
Общие требования к выполнению контрольной работы
Контрольная работа по курсу «Логистика» выполняется для закрепления знаний и навыков применения методов логистики. При самостоятельном изучении… Задания к контрольной работе составлены в 10 вариантах. Каждый студент… Расчеты должны быть представлены в развернутом виде со всеми формулами, пояснениями и выводами, соблюдая достаточную…Основные понятия логистики
Понятие материального потока является ключевым в логистике. Материальные потоки образуются в результате транспортировки, погрузки, разгрузки и выполнения других операций с сырьем, полуфабрикатами и готовыми изделиями.
Материальный поток – совокупность материальных ценностей, находящихся в процессе приложения к ним различных логистических операций.
Рассмотрим схему материального потока, начиная от первичного источника сырья вплоть до конечного потребителя (рис. 1). Весь путь движения материалов на этой схеме можно разделить на два участка:
- на первом участке движется продукция производственно-технического назначения;
- на втором – изделия народного потребления.
Качественный состав потока по мере продвижения по цепи меняется. Вначале между источником сырья и первым перерабатывающим предприятием, а также между различными перерабатывающими производствами движутся, как правило, массовые однородные грузы. В конце цепи материальный поток представлен разнообразными товарами. Внутри отдельных производств также имеют место материальные потоки: между цехами или же внутри цехов перемещаются различные детали, заготовки, полуфабрикаты.

При классификации материальных потоков выделяют внешний и внутренний, входящий и выходящий материальные потоки.
Внешний материальный поток – это поток, который протекает во внешней по отношению к данной логистической системе среде.
Внутренний материальный поток – это поток, который протекает внутри данной логистической системы.
Входящий материальный поток – это внешний поток, входящий в данную логистическую систему.
Выходящий материальный поток – это поток, выходящий из данной логистической системы во внешнюю среду.
Информационный поток – это совокупность передаваемых сообщений, необходимых для управления материальным потоком.
Информационный поток соответствует материальному. В реальных логистических системах материальный и информационный потоки могут опережать друг друга. Информационный поток может иметь одинаковое направление с материальным (прямое) и противоположное ему (встречное). Опережающий информационный поток в прямом направлении содержит предварительные сообщения о предстоящем прибытии грузов, а во встречном направлении – сведения о заказе. Одновременно с материальным потоком параллельно ему идет информация о количественных и качественных параметрах перемещаемых грузов. Вслед за материальным потоком во встречном направлении может приходить информация о результатах приемки грузов, а также претензии и подтверждения.
Информационный поток характеризуется источником возникновения, объемом информации, скоростью передачи и т. д.
Логистическая операция – это действие, направленное на материальные ценности или информацию и порождающее материальный или информационный поток. К логистическим операциям с материальными ценностями можно отнести погрузку, разгрузку, транспортировку, упаковку и др. Логистические операции с информацией включают сбор, обработку и передачу соответствующей информации.
К логистическим функциямотносят конкретные задачи:планирование материального обеспечения производства, управление запасами, управление распределением продукции и др.
Логистическая цепь – это упорядоченное множество физических или юридических лиц, осуществляющих логистические операции в процессе движения материального потока от первичного источника сырья до конечного потребителя.
Основными звеньями логистической цепи являются:
- поставщики материалов;
- склады;
- транспорт;
- производители товаров;
- распределительные центры;
- потребители продукции.
Логистическая система представляет собой систему управления, выполняющую те или иные логистические функции. Она, как правило, состоит из нескольких подсистем и имеет связи с внешней средой. Различают макро- и микрологистические системы.
Микрологистическая система представляет собой логистическую систему промышленных, торговых, сервисных и других предприятий.
Макрологистическая система – это система управления материальными потоками, охватывающая предприятия и организации отрасли, региона, страны и т. д.
Методология и научная база логистики
Современная теория логистики базируется на методологиях целого ряда научных дисциплин: - математики (теория вероятностей, математическая статистика, теория случайных… - исследования операций и теории принятия решений: математическое программирование (линейное, нелинейное,…Анализ АВС
Управление в логистике характеризуется, как правило, большой номенклатурой управляемых объектов: широкий ассортимент товаров, большое число… Идея метода АВС состоит в том, чтобы из всего множества объектов выделить… В экономике широко известно так называемое правило Парето (20/80), согласно которому лишь пятая часть (20 %) от всего…Анализ XYZ
Анализ АВС позволяет дифференцировать ассортимент по степени вклада в конечный результат. Принцип дифференциации ассортимента в процессе анализа XYZ… В группу Х включают товары, спрос на которые равномерен, либо подвержен… В группу Y включают товары, которые потребляются в колеблющихся объемах. В частности, в эту группу могут быть включены…Задание 1.
Задача 1. В таблице приведены данные о прибыли (в тыс. р), которую приносят предприятию различные позиции номенклатуры.
| № позиции | Прибыль, тыс. р. |
Провести анализ АВС
1. Эмпирическим методом при YA=75 %, YA+B =95 %.
2. Дифференциальным методом при  ,
, 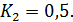
3. Аналитическим методом (графически)
Задача 2.
Исходные данные для проведения анализа XYZ приведены в таблице
| № позиции | Реализация за квартал, руб. | |||
1. Рассчитать коэффициенты вариации спроса по отдельным позициям ассортимента (cv).
2. Разделить анализируемый ассортимент на группы X, Y и Z.
Задачи закупочной логистики
Объектом логистики, как известно, является сквозной материальный поток, тем не менее, на отдельных участках управление им имеет свою специфику. В… Закупочная логистика управляет процессом обеспечения предприятий материальными… Целью логистики закупок является удовлетворение потребностей производства в материалах с максимально возможной…Методы определения потребностей
Необходимым условием эффективного управления материальными потоками является знание потребности на перспективу. Для ее определения могут… - детерминированные методы расчета в соответствии с планом производства и… - стохастические методы прогнозирования;Задание 2.
1. Рассчитать потребность в материале по данным таблицы
| Ассортимент | Программа производства, пар | Норма расхода материала, дм2 | Потребность в материале, дм2 |
| Сапоги мужские | |||
| Полуботинки мужские | |||
| Ботинки мужские | |||
| Сапоги женские | |||
| Ботинки женские | |||
| Туфли женские | |||
| Ботинки детские | |||
| Полуботинки детские | |||
| Итого |
2. Заводу технического стекла надо изготовить 25 000 штук изделия А и 10 000 штук изделия В при весе одного изделия соответственно 2 кг и 1 кг. Выход готовой продукции для всех материалов– 80 %. Рецептурный состав смеси представлен в таблице.
| Наименование материала | Содержание, % |
| Песок кварцевый | |
| Известь | |
| Окись натрия | |
| Окись магния | |
| Окись алюминия и железа | |
| Итого |
Рассчитать потребность в перечисленных материалах
Стохастические методы прогнозирования позволяют оценить ожидаемую потребность на основе временных рядов, характеризующих ее изменение на протяжении определенного промежутка времени. При этом используют прогноз по среднему значению, метод экспоненциального сглаживания и метод экстраполяции временного ряда.
Прогноз по среднему значению используется в условиях, когда потребность в материалах колеблется по месяцам при устойчивом среднем значении (отсутствие тренда).
Прогнозирование этим методом представляет собой процедуру усреднения известных значений потребности в материалах.
Экспоненциальное сглаживание временного ряда yt осуществляется по рекуррентной формуле
 , (7.4)
, (7.4)
где St- значение экспоненциальной средней в момент времени t;
a – параметр сглаживания (0<a<1);
b =1-a.
Выражение (7.4) можно переписать следующим образом

 . (7.5)
. (7.5)
В формуле (7.5) экспоненциальная средняя на момент времени t выражена как сумма экспоненциальной средней предшествующего периода St-1 и доли a разницы текущего значения временного ряда yt и экспоненциальной средней St-1.
Последовательное применение рекуррентной формулы (7.4) приводит к следующему выражению для St


 , (7.6)
, (7.6)
где n – число точек временного ряда;
S0 - некоторая начальная величина, необходимая для первого
применения формулы (7.4).
Из формулы (7.6) видно, что St оказывается взвешенной суммой всех уровней временного ряда. При этом веса падают экспоненциально с возрастанием «возраста» данных.
Экспоненциальная средняя St может быть использована не только для сглаживания временного ряда, но и для краткосрочного прогнозирования.
Прогнозная модель имеет вид
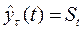 , (7.7)
, (7.7)
где  - прогноз, сделанный в момент времени t на t единиц времени вперед.
- прогноз, сделанный в момент времени t на t единиц времени вперед.
Отметим, что все свойства экспоненциальной средней распространяются на прогнозную модель. В частности, если St-1 рассматривать как прогноз на 1 шаг вперед в момент времени t-1, то величина yt-St-1 представляет собой погрешность этого прогноза, а новый прогноз St получается в результате корректировки предыдущего прогноза с учетом его ошибки по формуле (7.5). В этом и состоит суть адаптации.
При краткосрочном прогнозировании желательно с одной стороны быстро отразить изменение среднего уровня, а с другой – очистить ряд от случайных колебаний.
Для выполнения первого требования величину a следует увеличить, а для выполнения второго – уменьшить. Таким образом, эти два требования находятся в противоречии и необходим некий компромисс.
Рассмотрим вопрос выбора параметра a. При 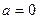 St= S0, т.е. адаптация полностью отсутствует, а при
St= S0, т.е. адаптация полностью отсутствует, а при  имеет место так называемая «наивная» модель прогнозирования
имеет место так называемая «наивная» модель прогнозирования
 ,
,
в соответствии с которой прогноз на любой срок равен текущему (последнему) значению временного ряда. В ряде работ рекомендовано брать значение a в пределах от 0,1 до 0,3, однако эта рекомендация по сути не имеет должного обоснования.
Выбор начального значения S0 всегда вызывает вопрос, однако величина 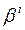 быстро убывает с ростом i и влияние S0 на величину St становится несущественным.
быстро убывает с ростом i и влияние S0 на величину St становится несущественным.
Пример.
Для иллюстрации процедуры расчета экспоненциальной средней рассмотрим пример сглаживания динамики курса акций фирмы IBM, производящей ЭВМ (табл. 4).
Т а б л и ц а 4. Экспоненциальные средние
| Номер точки | Исход-ный ряд | 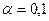
| 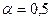
| 
| Номер точки | Исход-ный ряд | 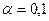
| 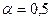
| 
|
| 506,4 | 508,0 | 509,6 | 505,7 | 513,3 | 513,1 | ||||
| 505,5 | 502,5 | 498,3 | 506,1 | 511,7 | 510,3 | ||||
| 505,3 | 503,2 | 503,4 | 506,1 | 508,8 | 506,4 | ||||
| 505,8 | 506,6 | 509,3 | 507,0 | 511,9 | 514,1 | ||||
| 506,1 | 507,8 | 509,0 | 508,5 | 517,0 | 521,2 | ||||
| 505,8 | 505,4 | 503,6 | 509,9 | 520,0 | 522,8 | ||||
| 505,2 | 502,7 | 500,4 | 511,6 | 523,5 | 526,6 | ||||
| 504,7 | 501,4 | 500,0 | 512,8 | 523,2 | 523,4 | ||||
| 504,2 | 500,7 | 500,0 | 514,3 | 525,6 | 527,5 | ||||
| 503,3 | 497,8 | 495,5 | 515,8 | 527,3 | 528,9 | ||||
| 502,4 | 495,9 | 494,2 | 518,0 | 532,7 | 537,1 | ||||
| 502,0 | 497,5 | 498,5 | 520,1 | 525,8 | 538,8 | ||||
| 502,0 | 499,7 | 501,2 | 522,2 | 538,4 | 540,8 | ||||
| 502,7 | 504,4 | 508,3 | 524,3 | 540,7 | 542,8 | ||||
| 505,0 | 514,7 | 523,3 | 525,9 | 540,9 | 541,2 |
При проведении расчетов начальное значение экспоненциальной средней S0 было принято равным средней арифметической из первых 5 уровней ряда

В нашем случае
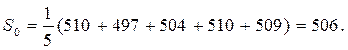
Дальнейшие вычисления при 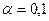 выглядят следующим образом
выглядят следующим образом


 и т. д.
и т. д.
Результаты вычислений экспоненциальных средних при a=0,1, a=0,5 и a=0,9 приведены в табл. 4.
Суть метода экстраполяции временного ряда состоит в распространении существующих закономерностей (тенденций и связей) на некоторый период в будущем. Динамическая (временная) экстраполяция основывается на предположении, что имеющийся временной ряд yt представляет собой сумму двух составляющих – регулярной и случайной.
y t = f (t) + e t , (7.8)
где f (t) - регулярная составляющая;
e t- случайная величина с нулевым математическим ожиданием.
В основе экстраполяционного метода лежит интуитивное представление о какой-то очищенной от помех сущности анализируемого процесса. Применение этого метода фактически сводится к построению наилучшего в некотором смысле описания регулярной составляющей и экстраполяции его на прогнозный момент времени.
Выбор типа функции f (t) осуществляется на основании визуального анализа динамики показателя. В качестве функций обычно используются:
- линейная f (t) = a0+ a1t (7.9)
- полиномиальная f (t) = a0+ a1t + a2t2 + .... + antn; (7.10)
bt
- экспоненциальная f (t) = a e ; (7.11)
a
- логистическая кривая f(t) = --------------------- (7.12)
-ct
1 + b e
и другие простые математические зависимости.
Методы экстраполяции целесообразно использовать при прогнозировании показателей в тех случаях, когда имеется достаточно представительная статистика, позволяющая провести построение временных рядов, причем прогнозируемые события должны носить массовый характер.
Методы экспертного прогнозирования используют индивидуальные или групповые мнения о перспективах развития прогнозируемого объекта и могут использоваться при отсутствии или сложности получения статистической информации.
Индивидуальные экспертные оценки основаны на использовании мнений экспертов, полученных независимо друг от друга. Напротив, методы коллективных экспертных оценок, например, "мозговой атаки" (коллективной генерации идей) основываются на всестороннем обсуждении ситуации членами группы. Промежуточное положение занимают анкетные методы с обратной связью, такие как "Дельфи". Достоинством этой группы методов является наличие влияния мнений одних экспертов на других за счет переосмысливания первоначальных суждений на основе анализа высказываний других экспертов.
Комбинированная прогнозная оценка
- установить область, внутри которой прогнозные результаты, полученные разными методами, можно считать непротиворечивыми; - получить аналитическое выражение для комбинированной прогнозной оценки. В комбинированной оценке может участвовать несколько прогнозов , полученных разными методами, если эти прогнозы не…Задание 3.
1. Сделайте прогноз потребности в материалах на следующий месяц методом экспоненциального сглаживания, если прогноз на текущий месяц составил 650 единиц, однако фактически потребовалось только 550. Параметр сглаживания α равен 0,3.
2. Прогнозы, полученные методом экстраполяции и экспертным методом составили соответственно 560 и 580 единиц продукции, средняя квадратическая ошибка этих прогнозов соответственно 35 и 45 единиц. Построить комбинированный прогноз и найти его дисперсию.
Оценка и выбор поставщиков
Основными источниками сведений о поставщиках и материалах являются личные контакты с продавцами, объявления в рекламных изданиях, описания товаров в… В результате изучения всех источников составляется список поставщиков, имеющих… На выбор поставщика существенное влияние оказывают результаты работы по уже заключенным договорам. При этом…Задание 4.
1. В течение определенного периода предприятие получало от трех поставщиков одну и ту же продукцию. Руководство предприятия приняло решение в будущем ограничиться услугами одного поставщика. Данные для расчета рейтинга поставщиков приведены в таблице.
| Критерий выбора | Вес критерия | Оценка критериев по 10-балльной шкале | ||
| Поставщик А | Поставщик Б | Поставщик В | ||
| Надежность поставки | 0,30 | |||
| Цена | 0,25 | |||
| Качество товара | 0,15 | |||
| Условия платежа | 0,15 | |||
| Возможность расширения поставок | 0,10 | |||
| Финансовое состояние | 0,05 | |||
| ИТОГО | 1,00 |
Какой из поставщиков имеет наибольший рейтинг?
Задачи управления запасами
Задачи управления запасами можно разделить на две группы: - задачи создания и поддержания запасов материальных ресурсов в каналах… - задачи создания и поддержания запасов готовой продукции в каналах распределения.Классическая детерминистическая модель управления запасами
Рассмотрим одну из классических и наиболее распространенных на практике оптимизационных моделей управления запасами. Эта модель предполагает следующие допущения:
- спрос (расход) является детерминированным и постоянным
( a(t)=a=const);
- период между двумя смежными заказами (поставками) постоянен
( );
);
- спрос удовлетворяется полностью и мгновенно ( );
);
- страховой запас отсутствует;
- емкость склада не ограничена;
- затраты на выполнение заказа (с0) и цена поставляемой продукции в течение планового периода постоянные;
- затраты на хранение единицы запаса в течение года постоянные и равны ch.
Критерием оптимизации размера заказа на пополнение запасов в данной модели является минимум общих затрат на выполнение заказов и хранение запаса на складе в течение планового периода, например, года.
Определим суммарные затраты в модели управления запасами  . Предположим, что годовая потребность в материальных ресурсах равна D, а объем партии поставки q. Тогда за год необходимо сделать D/q поставок на пополнение запаса, а годовые затраты на выполнение заказов будут равны
. Предположим, что годовая потребность в материальных ресурсах равна D, а объем партии поставки q. Тогда за год необходимо сделать D/q поставок на пополнение запаса, а годовые затраты на выполнение заказов будут равны
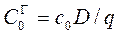 . (10.1)
. (10.1)
Затраты на хранение запасов на складе в течение года можно определить по формуле
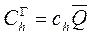 , (10.2)
, (10.2)
где 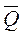 - средняя величина запаса, поддерживаемая на складе.
- средняя величина запаса, поддерживаемая на складе.
Затраты 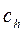 могут быть выражены в долях (или процентах) от стоимости единицы продукции. Тогда
могут быть выражены в долях (или процентах) от стоимости единицы продукции. Тогда
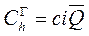 , (10.3)
, (10.3)
где с – цена единицы продукции, хранимой на складе;
i – доля от цены, приходящаяся на затраты по хранению запасов.
Средняя величина запаса 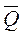 будет равна q/2.
будет равна q/2.
Тогда для суммарных годовых затрат получим
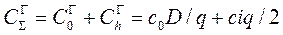 , (10.4)
, (10.4)
Оптимальный размер заказа q* будет соответствовать минимуму суммарных затрат в точке, где 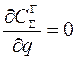 .
.
Возьмем производную выражения (10.4) и приравняем ее нулю:
 (10.5)
(10.5)
Решая уравнение (10.5) относительно q, получим:
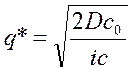 . (10.6)
. (10.6)
В оригинале формула для оптимального размера заказа была получена Ф.У. Харрисом в 1913 г., однако в теории управления запасами она больше известна как формула Уилсона.
Оптимальное количество заказов за год N* и интервал времени между двумя смежными заказами  будут соответственно равны:
будут соответственно равны:
 ; (10.7)
; (10.7)
 (дней). (10.8)
(дней). (10.8)
Рассмотрим пример 1.
Исходные данные для расчета приведены в таблице
| Параметры | D, штук | c0, руб | i, % | c, руб |
| Величина | 60,8 | 22,0 | 29,3 |
Для определения q* используем формулу (10.6)
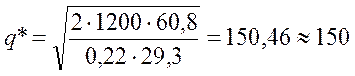 .
.
Таким образом, оптимальная величина заказа (партии поставки) будет равна 150 единиц продукции.
По формуле (10.7) определим оптимальное количество заказов за год
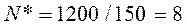 заказов.
заказов.
Оптимальное время между двумя смежными заказами будет равно
 дней.
дней.
Задание 5
Задача 1.
Ежедневный спрос на некоторый продукт составляет 100 ед. Затраты на приобретение каждой партии этого продукта, не зависимые от объема партии, равны 100 $, а затраты на хранение продукта – 0,02 $ в сутки. Определить оптимальный объем партии и интервал между поставками.
Задача 2.
Потребность сборочного предприятия в деталях некоторого типа составляет D деталей в год, причем эти детали расходуются в процессе производства равномерно и непрерывно. Детали поставляются партиями равного объема. Хранение детали на складе стоит ch руб в сутки, а поставка партии c0.
| Хар-ка | Номер варианта | |||||||||
| D | ||||||||||
| c0 | ||||||||||
| ch | 0,35 | 0,4 | 0,42 | 0,37 | 0,41 | 0,38 | 0,33 | 0,34 | 0,36 | 0,39 |
Определить наиболее экономичный объем партии и интервал между поставками.
Задача 3.
По условиям предыдущей задачи определить, на сколько процентов увеличатся затраты на создание и хранение запаса по сравнению с минимальными затратами при объеме заказываемых партий – 1000 деталей.
Важную роль в теории управления запасами для моделей с  играет определение момента заказа (tз) или такого уровня (Qз), когда необходимо делать заказ.
играет определение момента заказа (tз) или такого уровня (Qз), когда необходимо делать заказ.
Точка заказа может быть определена с использованием параметра величины спроса (a) по формуле
 . (10.9)
. (10.9)
Если в условиях предыдущего примера предположить, что  дней, и, учитывая, что a=D/365, получим
дней, и, учитывая, что a=D/365, получим
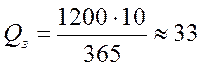 ед.
ед.
Таким образом, мы должны подавать заказ на пополнение запаса, когда уровень запаса на складе снизится до 33 единиц товара.
В тех случаях, когда время транспортировки заказа на склад занимает большую часть времени его выполнения 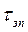 и сопоставимо с циклом пополнения запаса
и сопоставимо с циклом пополнения запаса  , необходимо учитывать затраты, связанные с обслуживанием запаса в пути.
, необходимо учитывать затраты, связанные с обслуживанием запаса в пути.
Классическая модель не учитывает эти затраты. Рассмотрим модернизированную модель, учитывающую затраты на запасы в пути с целью возможного выбора способа доставки из нескольких видов транспорта.
Введем следующие обозначения:
сп – затраты, связанные с запасом в пути на единицу продукции в год;
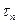 - время в пути;
- время в пути;
 - средняя величина запаса в пути.
- средняя величина запаса в пути.
Среднюю величину запаса в пути можно определить по формуле
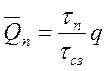 . (10.10)
. (10.10)
С учетом приведенных выше обозначений и формулы (10.10) суммарные затраты будут равны
 . (10.11)
. (10.11)
Если по аналогии с затратами ch представить затраты cп в долях (j) от цены единицы товара, то формула (10.11) примет вид
 . (10.12)
. (10.12)
Рассмотрим пример 2.
Пусть в условиях примера 1 у фирмы есть возможность выбора доставки заказа на склад железной дорогой или автомобильным транспортом при следующих исходных данных:
- время доставки заказа по железной дороге равно 10 дней, а автомобильным транспортом – 7 дней:
- тарифы за единицу груза равны: железной дорогой – 0,6 д.е., автомобильным транспортом – 0,9 д.е.
Предположим, что затраты ct составляют j=10% от цены товара. Рассчитаем затраты по двум вариантам транспортировки по формуле (10.12):
- железной дорогой
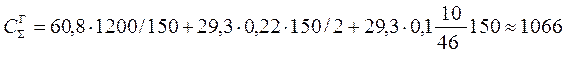 д.е.
д.е.
- автомобильным транспортом
 д.е.
д.е.
Рассчитаем общие годовые затраты, связанные с управлением запасами, с учетом затрат на транспортировку
- железной дорогой
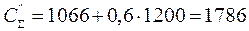 д.е.
д.е.
- автомобильным транспортом
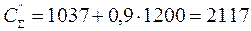 д.е.
д.е.
Таким образом, по критерию суммарных затрат более выгодным оказался вариант транспортировки продукции на склад по железной дороге.
Рассмотрим теперь влияние неопределенности параметров на принимаемые решения по управлению запасами.
Классическая модель является идеализированной схемой, иллюстрирующей процесс управления запасами при полностью детерминированных параметрах. На практике постоянно приходится сталкиваться с различными ситуациями, вызывающими неопределенность параметров спроса, заказа и поставок. Эта неопределенность объясняется как самой стохастической природой некоторых параметров, например, величины спроса a, так и влиянием различных рисков.
Если предположить, что параметры управления запасами Qз, qп, tсз были определены для классической модели при средней интенсивности спроса 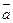 , а реальный спрос
, а реальный спрос 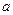 является случайной величиной, распределенной по нормальному закону с дисперсией s2(a), то плотность распределения вероятностей величины Qз будет иметь вид, представленный на рис. 4.
является случайной величиной, распределенной по нормальному закону с дисперсией s2(a), то плотность распределения вероятностей величины Qз будет иметь вид, представленный на рис. 4.

На графике показано, что разброс возможных значений Qз вокруг среднего 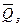 для нормального закона распределения с вероятностью Р=0,997 укладывается в диапазон (
для нормального закона распределения с вероятностью Р=0,997 укладывается в диапазон (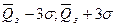 ) по правилу «трех сигм».
) по правилу «трех сигм».
При этом
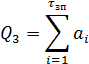
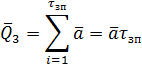
а дисперсия и среднее квадратическое отклонение Qз составят


Неопределенность исходных параметров систем управления запасами вызывается также многочисленными рисками, например, в сроках доставки продукции, объемах поставок, качестве, ассортименте; рисками, связанными со стихийными бедствиями, возможностью хищений, пожаров, естественной убыли и т. п. Связанная с этими причинами неопределенность также может вызвать явление дефицита, причем неопределенными (стохастическими) могут быть все параметры модели управления запасами или их отдельные комбинации.
Для исключения возможности возникновения дефицита создаются страховые запасы. Определение величины страхового запаса Qстр производится обычно на основе методов математической статистики. Для рассматриваемой модели величина точки заказа будет равна
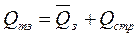 . (10.14)
. (10.14)
Наиболее простой способ расчета страхового запаса заключается в расчете доверительного интервала для Qз по формуле
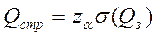 , (10.15)
, (10.15)
где  - табличное значение функции Лапласа;
- табличное значение функции Лапласа;
 - среднее квадратическое отклонение точки заказа.
- среднее квадратическое отклонение точки заказа.
Параметр  определяется по величине доверительной вероятности
определяется по величине доверительной вероятности  , где
, где  - уровень значимости.
- уровень значимости.
Пример. В условиях примера 1 рассчитаем страховой запас при следующих дополнительных исходных данных:
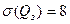 ;
; 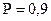 .
.
По таблицам функции Лапласа находим, что  =1,65. Подставляя найденное значение в формулу (10.15), получим
=1,65. Подставляя найденное значение в формулу (10.15), получим
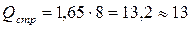 ед.
ед.
Точка заказа будет соответственно равна
 ед.
ед.
Стохастические модели управления запасами
Предположим, что спрос r за интервал времени Т является случайным и задан его закон (ряд) распределения p(r) или плотность распределения… В качестве функции суммарных затрат, являющейся в стохастических моделях… В рассматриваемой модели при дискретном случайном спросе r, имеющем закон распределения p(r), математическое ожидание…Задание 6
Задача 1.
Имеющиеся на складе изделия расходуются в течение месяца. Затраты на хранение одного изделия составляют 5 д. ед., а штраф за дефицит одного изделия – 100 д. ед. Закон распределения спроса представлен в таблице
| Спрос r | 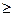 6 6
| ||||||
| Вероятность p(r) | 0,1 | 0,2 | 0,2 | 0,3 | 0,18 | 0,02 |
Найти оптимальный месячный запас склада.
Задача 2.
Решить предыдущую задачу в предположении непрерывного случайного спроса r, распределенного по показательному закону с функцией распределения вероятностей
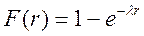 при
при  =0,98.
=0,98.
Складская логистика
Складская логистика решает следующие задачи: - выбор формы складирования; - определение количества складов и размещение складской сети;Оценка работы складов
Складской товарооборот – показатель, характеризующий количество реализованной продукции за соответствующий период (месяц, квартал, год) со склада… Складской грузооборот определяется количеством отпущенных (отправленных)… Коэффициент оборачиваемости материалов (Коб)- это отношение годового (квартального) грузооборота материалов к среднему…Задание 7
Задача 1.
Фирма вынуждена хранить свою продукцию на складе со следующими потребностями в площадях (по кварталам):
1 кв. – 50 000 м2;
2 кв. – 100 000 м2;
3 кв. - 150 000 м2;
4 кв. – 100 000 м2.
Затраты на строительство склада включают в себя постоянные затраты FC= 500 000 $ и переменные затраты – 10 $ за каждый м2. Эксплуатация собственного склада потребует 0,1 $ за м2 в год. Аренда и использование чужого склада – 0,75 $ за м2 в год.
Стоит ли строить собственный склад площадью 150 000 м2 при сроке эксплуатации 30 лет ?
Задача 2.
Необходимо расположить склад для обслуживания 7 заказчиков. Координаты месторасположения заказчиков и средний спрос за неделю, выраженный в числе отправляемых автомобилей с продукцией, представлены в таблице.
| Заказчик | Координаты месторасположения | Средний спрос за неделю |
| 100,110 | ||
| 120,130 | ||
| 200,150 | ||
| 180,210 | ||
| 140,170 | ||
| 130,180 | ||
| 170,80 |
Найти координаты оптимального места расположения склада.
Задача 3.
Остатки продукции на складе на начало года составили 135 683 шт. , приход за год – 481 930 шт., остаток на конец года – 117 481 шт. Рассчитать средний складской запас, грузооборот и коэффициент оборачиваемости.
Задачи транспортной логистики
Управление материальным потоком в процессе транспортировки и организация транспортирования грузов являются сферой транспортной логистики.
Транспортная логистика решает следующие задачи:
- создание транспортных систем;
- обеспечение технологического единства транспортно-складского процесса;
- выбор способа транспортировки и транспортного средства;
- определение оптимальных маршрутов доставки.
Выбор транспортного средства
Основой выбора вида транспорта, оптимального для конкретной перевозки, служит информация о характерных особенностях различных видов транспорта. Существуют следующие виды транспорта: - железнодорожный;Составление оптимальных маятниковых маршрутов
Схема маятникового маршрута с указанием расстояний ( в км) приведена на рис.8.Составление оптимальных маршрутов (транспортная задача)
Рассмотрим классическую транспортную задачу – задачу распределения грузов, имеющихся у поставщиков, между потребителями с целью минимизации суммарных транспортных издержек.
Пусть имеется m поставщиков и n потребителей некоторой продукции. Известны имеющиеся количества груза у поставщиков ai>0 (i=1,…,m), потребности потребителей bj>0 (j=1,…,n) и стоимости перевозки единицы продукта от каждого поставщика каждому потребителю – cij (i=1,…,m; j=1,…,n).
Требуется найти план перевозок, т. е. указать сколько единиц продукции каждый поставщик должен доставить каждому потребителю, чтобы суммарная стоимость перевозок была минимальной.
Если суммарное количество груза у поставщиков равно суммарной потребности потребителей, т. е.
 ,
,
то транспортная задача называется закрытой, в противном случае – открытой.
Условия транспортной задачи можно представить в виде таблицы
| b1 | b2 | … | bn | |
| a1 | c11 | c12 | … | c1n |
| a2 | c21 | c22 | … | c2n |
| … | … | … | … | … |
| am | cm1 | cm2 | … | cmn |
Пусть xij – количество единиц продукции, перевозимое от i- го поставщика j- му потребителю. План перевозок можно представить в виде матрицы
x11 x12 …… x1n
x21 x22 …… x2n
X = …………………………….
xm1 xm2 …… xmn
Условия задачи имеют вид
 (i=1,…,m) (17.1)
(i=1,…,m) (17.1)
 (j=1,…,n)
(j=1,…,n)
 (i=1,…,m ; j=1,..,n) (17.2)
(i=1,…,m ; j=1,..,n) (17.2)
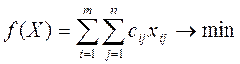 (17.3)
(17.3)
Задача (17.1 – 17.3) называется транспортной задачей. Для ее решения используется метод потенциалов.
Критерий оптимальности плана перевозок заключается в следующем: для того, чтобы план перевозок Х* был оптимальным, необходимо и достаточно, чтобы существовали числа: u1, u2, …,um – потенциалы поставщиков, v1, v2, ….,vn – потенциалы потребителей, удовлетворяющие двум условиям:
1)  (i=1,…,m ; j=1,…,n)
(i=1,…,m ; j=1,…,n)
2) если xij>0, то 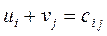
Алгоритм метода потенциалов заключается в следующем:
- построение исходного плана перевозок методом «северо-западного» угла;
- проверка построенного плана на оптимальность при помощи критерия;
- улучшение плана, т. е. построение нового плана с меньшей стоимостью перевозок.
Алгоритм метода потенциалов применяется к закрытой транспортной задаче. Любую открытую задачу можно преобразовать в закрытую путем введения фиктивного поставщика или фиктивного потребителя.
Рассмотрим следующий пример. Пусть имеется 3 поставщика и 3 потребителя некоторой продукции. Мощности поставщиков, потребности потребителей и стоимости перевозки единицы продукции от каждого поставщика каждому потребителю заданы в таблице
| ai / bj | |||
Требуется найти такой план перевозок, при котором суммарная стоимость будет минимальной.
Прежде всего, подсчитаем суммарную мощность поставщиков и суммарную потребность потребителей


Так как 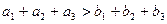 , то задача является открытой и для сведения ее к закрытой введем фиктивного потребителя с потребностью
, то задача является открытой и для сведения ее к закрытой введем фиктивного потребителя с потребностью

Стоимости перевозки единицы продукции от каждого поставщика фиктивному потребителю положим равными нулю. В результате получим закрытую транспортную задачу, условия которой содержатся в таблице
Решим полученную закрытую транспортную задачу методом потенциалов.
Составим исходный план перевозок Х1 методом «северо-западного угла», распределяя мощности поставщиков по порядку между потребителями так, чтобы каждая перевозка была максимально возможной. У 1-го поставщика имеется 25 единиц продукции, а первому потребителю нужно 20 единиц, следовательно, ему нужно направить 20 единиц, т. е. х11=20. Оставшиеся у первого поставщика 5 единиц направим второму потребителю, т. е. положим х12=5. Недостающие второму потребителю 5 единиц продукции направим ему от второго поставщика, т. е. х22=5. Аналогично положим х23=10, х33=20, х34=15. Остальные перевозки равны нулю.
План перевозок оформим в виде таблицы, разделенной на клетки. В каждой клетке поместим перевозки хij. В клетки, соответствующие нулевым перевозкам, нули не вписываем, оставляя их пустыми. В таком случае план перевозок Х1 будет иметь вид
Х1=
При описанном выше способе распределения продукции план Х1 будет содержать не более, чем m+n-1 положительных перевозок или занятых клеток, где m - число поставщиков, n - число потребителей продукции. Остальные компоненты плана Х1, соответствующие нулевым перевозкам, будем называть свободными клетками. Если число занятых клеток k=m+n-1, то план перевозок называется невырожденным, если k<m+n-1, то вырожденным.
Для плана Х1 имеем k=6, m+n-1=6, следовательно план Х1 является невырожденным.
Заметим, что если план перевозок является вырожденным, то следует часть свободных клеток считать занятыми, записав в них нули, так, чтобы общее число занятых клеток было равно m+n-1. В дальнейшем с этими нулями следует обращаться как с положительными перевозками.
Подсчитаем суммарную стоимость перевозок по плану Х1:
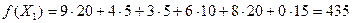 .
.
Проверим план Х1 на оптимальность Найдем потенциалы u1, u2, …,um поставщиков и потенциалы v1, v2, ….,vn потребителей.
По условию 2 для занятых клеток
 ,
, 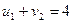 ,
,  ,
,  ,
,  ,
, 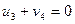 . (17.4)
. (17.4)
Один из потенциалов всегда задается произвольно, например, зададим 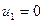 . Тогда из системы (17.4) получим
. Тогда из системы (17.4) получим 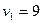 ,
, 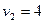 ,
, 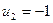 ,
,  ,
,  ,
,  .
.
По условию 1 для свободных клеток
 ,
,  ,
, 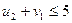 ,
, 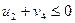 ,
,  ,
,  . (17.5)
. (17.5)
Подставив потенциалы, найденные из уравнений (17.4) в неравенства (17.5), получим
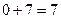 ,
, 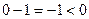 ,
,  ,
, 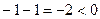 ,
,  ,
,  .
.
Мы видим, что не выполняются два неравенства
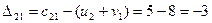 ,
,
 .
.
Следовательно, план Х1 можно улучшить, введя в план перевозку  , для которой разность
, для которой разность  оказалась меньше разности
оказалась меньше разности 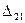 . С этой целью составим так называемый цикл, имеющий начало в свободной клетке (3,1), а остальные вершины – в занятых клетках, последовательно увеличивая и уменьшая перевозки, попавшие в цикл, на величину
. С этой целью составим так называемый цикл, имеющий начало в свободной клетке (3,1), а остальные вершины – в занятых клетках, последовательно увеличивая и уменьшая перевозки, попавшие в цикл, на величину 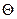 . В результате получим план
. В результате получим план 
 =
=
20-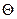
| 5+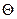
| ||
5-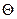
| 10+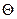
| ||
+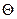
| 20-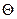
|
Важно отметить, что при составлении цикла следует двигаться только по горизонтали или вертикали, так, чтобы в каждую строку и каждый столбец плана перевозок, охваченных циклом, попали только две перевозки.
Выберем 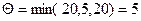 , то есть в качестве
, то есть в качестве 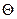 выбирается наименьшая из перевозок, из которых
выбирается наименьшая из перевозок, из которых 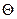 вычитается. При включении в план Х1 перевозки
вычитается. При включении в план Х1 перевозки 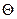 =5, суммарная стоимость перевозок изменится на
=5, суммарная стоимость перевозок изменится на
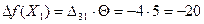 , то есть уменьшится на 20 единиц и для нового плана Х2 составит
, то есть уменьшится на 20 единиц и для нового плана Х2 составит
 .
.
Пересчитав перевозки, вошедшие в цикл плана  при
при 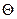 =5, получим новый план перевозок Х2.
=5, получим новый план перевозок Х2.
Х2=
План Х2 лучше плана Х1 , так как стоимость перевозки 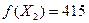 по плану Х2 оказалась меньше стоимости перевозок
по плану Х2 оказалась меньше стоимости перевозок 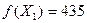 по плану Х1.
по плану Х1.
Проверим на оптимальность план Х2. Для этого составим систему уравнений для занятых клеток плана Х2
 ,
, 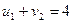 ,
,  ,
,  ,
,  ,
, 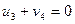 .
.
Из этой системы при 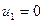 получим:
получим: 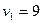 ,
, 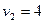 ,
,  ,
,  ,
, 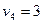 ,
, 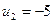 .
.
Проверим выполнение неравенств для свободных клеток плана Х2.
 ,
, 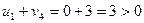 ,
, 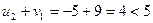 ,
,
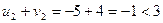 ,
, 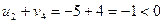 ,
, 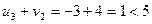 .
.
Не выполняются два неравенства, причем 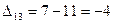 ,
,  . Следовательно, план Х2 можно улучшить, введя в план перевозку
. Следовательно, план Х2 можно улучшить, введя в план перевозку  . Составив цикл для свободной клетки (1,3), получим план
. Составив цикл для свободной клетки (1,3), получим план 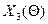 . Выбрав
. Выбрав  , получим
, получим
 ,
,
и стоимость перевозок для нового плана Х3 составит
 .
.
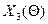 =
=
15-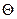
| +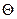
| ||
5+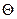
| 15-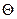
|
При 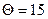 план
план 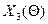 преобразуется в новый план Х3. Так как
преобразуется в новый план Х3. Так как 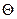
 совпадает с двумя перевозками, а только одна из занятых клеток должна перейти в число свободных, то в клетку (3,3) записываем 0 и считаем ее занятой.
совпадает с двумя перевозками, а только одна из занятых клеток должна перейти в число свободных, то в клетку (3,3) записываем 0 и считаем ее занятой.
Х3=
Для занятых клеток плана Х3:
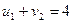 ,
, 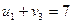 ,
,  ,
,  ,
,  ,
, 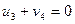 .
.
Из этой системы при 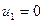 получим:
получим: 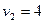 ,
,  ,
, 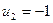 ,
,  ,
, 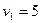 ,
,  .
.
Для свободных клеток плана Х3:
 ,
,  ,
, 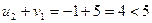 ,
,
 ,
, 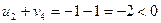 ,
,  .
.
Таким образом, выполняются оба условия (1 и 2) оптимальности плана перевозок. Следовательно, план перевозок Х3 является оптимальным планом закрытой задачи, а  представляет собой наименьшую стоимость перевозок. Отбросив последний столбец плана Х3, получим оптимальный план Х* исходной открытой задачи. Отброшенный столбец означает, что первые два поставщика вывезут всю имеющуюся у них продукцию, а у третьего поставщика останутся не вывезенными 15 единиц продукции.
представляет собой наименьшую стоимость перевозок. Отбросив последний столбец плана Х3, получим оптимальный план Х* исходной открытой задачи. Отброшенный столбец означает, что первые два поставщика вывезут всю имеющуюся у них продукцию, а у третьего поставщика останутся не вывезенными 15 единиц продукции.
Задание 9.
Решить транспортную задачу. Заданы мощности поставщиков ai (i=1,…,m), потребности потребителей bj (j=1,…,n) и стоимости перевозки единицы продукта от каждого поставщика каждому потребителю – cij (i=1,…,m; j=1,…,n). Требуется найти план перевозок, при котором суммарные транспортные затраты будут наименьшими по вариантам:
1 вариант.
2 вариант.
3 вариант.
4 вариант.
5 вариант.
6 вариант.
7 вариант.
8 вариант.
9 вариант.
10 вариант.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Чеботаев А.А. Логистика и маркетинг : Маркетологистика. – М. : Экономика, 2005. – 246 с.
2. Модели и методы теории логистики: Учебное пособие / Под ред. В.С. Лукинского, 2-е изд. – СПб.: Питер, 2008. – 448 с.
3. Слюсарева Е. В. Логистика: учебное пособие.- Омск : изд-во ОмГТУ, 2007.- 27 с.
4. Тяпухин А. П. Логистика: учебное пособие для студентов вузов.- Оренбург: ГОУВПО «ОГИМ», 2005.- 109 с.
5. Иванов М. Ю. Логистика: учебное пособие.- М.: РИОР, 2006.- 89 с.
6. Леонтьев В. Б. Основы логистики: учебное пособие по курсу.- М.: МИЭТ, 2007.- 71 с.
Содержание
| 1.История возникновения и эволюция термина «Логистика» | |
| 2. Основные понятия логистики | |
| 3. Методология и научная база логистики | |
| 4. Анализ АВС | |
| 5. АнализXYZ | |
| 6. Задачи закупочной логистики | |
| 7. Методы определения потребностей | |
| 8.Оценка и выбор поставщиков | |
| 9. Задачи управления запасами | |
| 10. Классическая детерминистическая модель управления запасами | |
| 11. Стохастические модели управления запасами | |
| 12. Складская логистика | |
| 13. Оценка работы складов | |
| 14. Задачи транспортной логистики | |
| 15. Выбор транспортного средства | |
| 16. Составление оптимальных маятниковых маршрутов | |
| 17. Составление оптимальных маршрутов (транспортная задача) | |
| БИБЛИОГРАФИЧЕСКИЙ СПИСОК |
– Конец работы –
Используемые теги: технологии, дизайна0.029
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Технологии и дизайна
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов