ОБРАЗОВАНИЕ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПРОСТРАНСТВЕННЫХ ФЕРМ
Пример 7.1. На рис. 7.1 изображена пространственная ферма, для которой У=12, Сф = 30, Со = 6; поэтому по формуле (7.1) W = 3-12—30—6 = 0, следовательно, ферма геометрически неизменяема и неподвижна.
С другой стороны, все грани фермы представляют собой трехугольники, т. е. данная система является сетчатой, прикрепленной к земле шестью опорными стержнями. Поэтому о ней можно сразу сказать, не интересуясь числом стержней и узлов, что она геометрически неизменяема и не имеет лишних стержней.
Пример 7.2. Фермы, приведенные на рис. 7.2, представляют собой сетчатые системы, прикрепленные к земле шестью стержнями.
Первая ферма (рис. 7.2, а) геометрически неизменяема и не имеет ишних стержней. Вторая же ферма, изображенная на рис. 7.2, б, является мгновенно изменяемой. Действительно, четыре опорных стержня этой фермы параллельны, а два других пересекаются, в одной
Рис. 7.1
точке А, поэтому прямая 1—1, проходящая через бесконечно удаленную точку и точку А, является осью вращения, вокруг которой возможен бесконечно малый поворот всей системы.
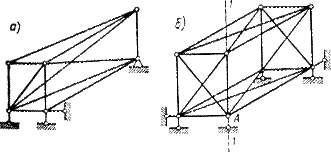
Рис. 7.2
Пример7.3. Рассмотрим ферму, изображенную на рис. 7.3.Имеет W=3∙18 – 36 – 18 = 0, т. е. данная ферма содержит достаточное для неизменяемости число связей. Для кинематического анализа рассмотрим способ образования этой фермы.
|
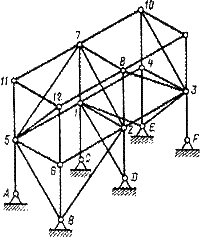Опорные точки фермы A, B, Cнеподвижны, поскольку прикреплены к земле каждая тремя опорными стержнями. Узел 1 присоединяется к земле триадой — тремя стержнями 1—С, 1—D, 1– Е; следовательно, эти три стержня образуют жесткий неизменяемый диск. К этому диску и к земле при помощи триады (стержней 1—2, 2—В, 2—D) присоединен узел 2. Обходя последовательно узлы 3, 4, 5, 6, убеждаемся, что все они неподвижны, поскольку прикрепляются к неподвижным дискам и к земле при помощи триад. Итак, нижний ярус фермы неподвижен. Узел 7 присоединяется к неподвижному нижнему ярусу фермы посредством трех стержней 7—1, 7—5, 7—2, не лежащих в одной плоскости, и не- подвижен. Обходя далее последовательно узлы 8, 10, 9, 12, 11, убеждаемся, что все они присоединяются к неподвижным дискам и к нижнему ярусу фермы посредством триад и поэтому неподвижны. Итак, система геометрически неизменяема.
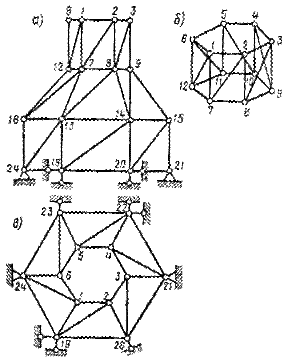
Пример 7.4. Исследуем геометрическую структуру фермы, представленной на рис. 7.4, а. Прежде всего воспользуемся формулой (7.1). Подсчитаем число узлов, стержней фермы и опорных связей: У=24, СФ= 60, Со= 12; поэтому W = 3∙24 — 60 — 12 = 0. Можно поступить и иначе. Чтобы данная система была сетчатой, ей недостает шести стержней: трех диагоналей в верхнем и трех в нижнем основаниях. Однако вместо недостающих стержней ферма имеет столько же дополнительных опорных стержней (общее число опорных стержней равно 12 вместо 6).
Итак, ферма имеет структуру, приемлемую для геометрически неизменяемой системы. Для дальнейшего анализа применим способ нулевой нагрузки. В узле 1 фермы (рис. 7.4, б, где представлена верхняя часть фермы) сходятся четыре стержня, три из которых лежат в одной плоскости; следовательно, при отсутствии внешней нагрузки в этом узле усилие в стержне 1—2 будет равно нулю. По тем же соображениям будет равно нулю и усилие в стержне 1—6 (при этом рассматривается равновесие узла 6). Очевидно, что усилия в остальных двух стержнях (1—7, 1—12), сходящихся в узле 1, также равны нулю. Переходя далее к узлам 2, 3 и т. д., убеждаемся, что усилия во всех стержнях верхней части фермы (за исключением стержней шестиугольника 7—12) равны нулю. Далее точно таким же образом рассмотрим работу нижней части фермы, начиная с узлов 7 и 12, переходя последовательно к узлам 8, 9 и т. д., при отсутствии внешней нагрузки. В результате найдем, что усилия во всех стержнях фермы, кроме стержней нижнего шестиугольника, равны нулю. Вырезая последовательно узлы нижнего шестиугольника, начиная, например, с 19 (рис. 7.4, в), легко убедиться, что равны нулю все реакции в опорных связях и усилия в стержнях шестиугольника. Итак, система действительно неподвижна и неизменяема.
|
