Основная система при расчете рам методом сил. Канонические уравнения
Порядок расчета.Рассмотрим порядок проверочного расчета статически неопределимой рамы на действие неподвижной нагрузки. При расчете рам произвольного очертания целесообразно от заданной статически неопределимой рамы переходить к основной статически определимой системе. Основной называют такую систему, которая принимается в основу расчета данной статически неопределимой конструкции. По основной системе устанавливают перемещения и усилия, по которым находят лишние неизвестные, применяя уравнения совместности перемещений, затем определяют окончательные усилия для заданной системы. Общий порядок расчета рамы методом сил следующий. От заданной статически неопределимой системы переходим косновной системе — статически определимой и неизменяемой, которая получается из заданной системы путем отбрасывания всех лишних связей (за исключением необходимых).
Заменяем отброшенные лишние связи соответствующими им силами, называемыми лишними неизвестными X1, X2, Х3 и т. д.
Составляем уравнения совместности перемещений, выражающие условия равенства нулю перемещений по направлению каждой лишней связи.
Определив все коэффициенты при неизвестных и свободные члены уравнений совместности перемещений, решаем систему этих уравнений и находим лишние неизвестные, после чего строим эпюры М, Q и N для рамы.
Уравнения совместности перемещений метода сил, написанные в определенной, раз навсегда установленной форме, называют каноническими уравнениями метода сил.
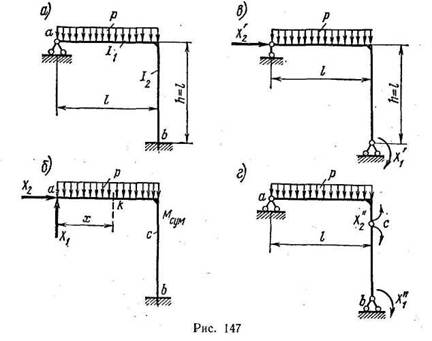
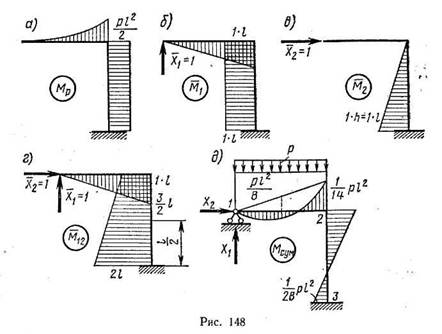
Рассмотрим порядок расчета простейшей несимметричной статически неопределимой рамы (рис. 147, а). В данном случае система дважды статически неопределима. От заданной статически неопределимой системы переходим к основной системе, отбрасывая шарнирно неподвижную опору (рис. 147,б). Получаем основную систему в виде рамы, защемленной правым концом, со свободным левым концом. Действие неподвижной опоры возмещаем силами X1 и Х2 — составляющими реакции неподвижной опоры. Это один из вариантов основной системы.
Можно предложить другой вариант основной системы — в виде двухопорной рамы; отбрасывая защемление правой опоры, заменяем ее действие моментом Х’1; ликвидируя горизонтальное закрепление левой опоры, возмещаем ее действие горизонтальной реакцией Х’1 (рис. 147, в)
И еще один вариант основной системы — в виде трехшарнирной рамы acb (рис. 147, г); действие лишних связей при этом возмещаем моментами Х”1 и Х"2 , где моменты Х"2 заменяют жесткую связь соседних сечений в заданной системе. Меняя положение шарнира с, получаем ряд вариантов основных систем.
Наиболее простой является основная система в виде защемленной рамы (рис. 147,6), для которой проще всего строится эпюра изгибающих моментов.
Выбрав основную систему и представив действие лишних связей неизвестными силами Х1 и Х2, составляем канонические уравнения.
 Каждое уравнение совместности перемещений, как было отмечено, выражает условие равенства нулю перемещения по направлению лишнего неизвестного. В заданной раме (рис. 147, а) вертикальное и горизонтальное перемещения центра неподвижной опоры а равны нулю. Те же условия должны выполняться и для основной системы (рис. 147,6). Условия равенства нулю вертикального и соответственно горизонтального перемещений точки а можно выразить так:
Каждое уравнение совместности перемещений, как было отмечено, выражает условие равенства нулю перемещения по направлению лишнего неизвестного. В заданной раме (рис. 147, а) вертикальное и горизонтальное перемещения центра неподвижной опоры а равны нулю. Те же условия должны выполняться и для основной системы (рис. 147,6). Условия равенства нулю вертикального и соответственно горизонтального перемещений точки а можно выразить так:
Δx1(x1x2 p)=0; Δx2(x1x2 p)=0; (2)
где Δx1(x1x2 p)— вертикальное перемещение точки а, т. е. перемещение по направлению силы Х1 от действия сил Х1, Х2 и нагрузки р; Δx2(x1x2 p)=0; — горизонтальное перемещение точки а по направлению силы Х2 от действия сил Х1, Х2 и нагрузки интенсивностью р.
Чтобы выразить уравнения (9.2) в явной форме через лишние неизвестные, применим известный из предыдущего принцип независимости действия: перемещение, вызванное системой сил, представим в виде суммы перемещений, вызванных отдельными силами X,, X, и нагрузкой интенсивностью р. Вместо уравнений (2) получим:
Δx1x1+Δx1x2+Δx1p=0; Δx2x1+Δx2x2+Δx2p=0;(3)
где первый индекс в выражении перемещения указывает, по направлению какой силы совершается перемещение, а второй индекс отмечает, какой силой вызвано перемещение.
Для краткости опустим в индексах при всех перемещениях букву х, оставив лишь номер лишнего неизвестного. Тогда вместо уравнений (3) получим
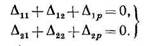 (4) (4)
|
Перемещения Δ1pи Δ2p, вызванные нагрузкой интенсивностью р, определяются в основной системе.
Для линейно-деформируемой упругой системы перемещения Δ12, Δ21, Δ22, вызванные силами Х1 и Х2, представляем по обобщенному закону Гука пропорциональными силами Х1 и Х2 соответственно:
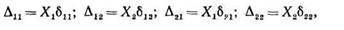
|
где δ11— перемещение по направлению силы X1 вызванное единичной силой Х1=1; δ12 — перемещение по направлению силы Х2, вызванное единичной силой Х2=1; δ22 — перемещение по направлению силы Х2, вызванное единичной силой Х2=1.
Уравнения деформаций (4) теперь можно представить в явной форме от лишних неизвестных:
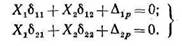 (5) (5)
|
Здесь δ11, δ 12, δ 21, δ 22— «единичные» перемещения; их легко определить по соответствующим эпюрам моментов, пользуясь формулами:
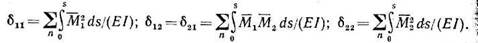 (6) (6)
|
В выражениях (6): М1 — функция изгибающего момента в произвольном сечении основной системы от Х1=1; М2 — изгибающий момент в том же сечении от X2=l; s — длина стержня рамы; п — число ее стержней.
|
Свободные члены уравнений (5), так называемые грузовые члены, определяют по общей формуле для перемещений:
 (7) (7)
|
При этом в формулах (6) и (7), как обычно при расчете рам, учтено лишь влияние на перемещения изгибающих моментов. Найдя выражения изгибающих моментов Мр , М1, и М2 и вычислив перемещения по формулам (6) и (7), решаем канонические уравнения деформаций (5) и находим лишние неизвестные Х1 и Х2. Если стержни рамы имеют переменное сечение, меняющееся от стержня к стержню, при решении уравнений (5) вводят соотношения моментов инерции сечений стержней.
Эпюры моментов Мр и от единичных неизвестных М1 и М2 даны
на рис. 148, а — в.