Свойства канонических уравнений. Построение эпюры моментов.
Отметим следующие свойства коэффициентов при неизвестных канонических уравнений:
1. Перемещения от единичных сил Х1=1 и Х2=1 с различными индексами равны между собой, т. е.
 (8) (8)
|
или, иначе, «единичные» перемещения не меняются от перестановки индексов—теорема о взаимности перемещений.
2. Перемещения от единичных сил X1 и Х2 с одинаковыми . индексами всегда положительны (δ11, δ 22), что непосредственно следует из выражений (6) для этих перемещений, содержащих квадраты изгибающих моментов.
«Единичные» перемещения с одинаковыми индексами δ11, δ22 называют главными, поскольку они не могут быть равны нулю и всегда входят в уравнения. «Единичные» перемещения с различными индексами δ12, δ21 называют побочными, так как при удачном выборе неизвестных они могут оказаться равными нулю. Если наметим линию, соединяющую в уравнениях (5) главные перемещения δ11 и δ22 (главная диагональ), то побочные перемещения, расположенные симметрично относительно главной диагонали, согласно равенству (8) должны быть равны между собой. Найдя из канонических уравнений лишние неизвестные Х1 и Х2, перейдем к построению эпюры моментов в заданной раме по основной системе. Эту эпюру называют окончательной эпюрой моментов Мсум. Ее ординату в произвольном сечении находим, пользуясь принципом сложения (см. рис. 147,б):
Мсум = Мp + Х1М1 + Х2 М2 (9)
По правой части выражения (9) момент в заданной статически неопределимой раме получается как сумма моментов от нагрузки Мр и от каждого лишнего неизвестного Xt и Х2. Увеличивая ординаты моментов от Х1 = 1 и Х2 = 1 соответственно в Х1 и Х2 раз и складывая этот результат с ординатой эпюры моментов только от нагрузки Мр (рис. 148,а), получаем ординаты окончательной эпюры Мсум (рис. 148,д). На этой эпюре показано, как найти момент в середине ригеля.
Проверка вычисления перемещений.В случае дважды статически неопределимой системы, решая систему уравнений (5), выражаем лишние неизвестные так:

|
где D — определитель системы, составленный из коэффициентов при неизвестных; D1, D2—определители системы, которые получаются путем замены соответствующего столбца членами Δ1p и Δ2p.
Существуют специальные способы решения системы линейных алгебраических уравнений вида (5), которые будут рассмотрены ниже.
Решение канонических уравнений в этом случае необходимо проводить с большой точностью, а каждую ступень вычислений подвергать тщательной проверке. Естественно избавиться от coвместности канонических уравнений и сводить решение к определению неизвестных из одного уравнения с одним неизвестным. Если в системе уравнений (5) будет δ 12 = 0, то для Xt получим такое решение:

|
Лишнее неизвестное здесь выражено отношением двух перемещений. Основная задача упрощения расчета сложных статически неопределимых систем и сводится к исключению совместности канонических уравнений путём специального выбора основной сиетемы и лишних неизвестных. Для решения системы уравнений успешно применяются электронные счетнорешающие машины и новые приемы решения системы линейных уравнений.
Отметим важность осуществления контроля всех операций расчета статически неопределимой системы, в особенности при наличии совместности уравнений. Проведем проверку расчета рамы, изображенной на рис. 147, а. Для отыскания всех перемещений, входящих в систему канонических уравнений, необходимо построить эпюры M1t М2 и Мр. Они изображены на рис. 148, а—в. Полагаем I1 = I2 = I. Проверив правильность построения всех эпюр, вычислим по правилу перемножения эпюр перемещения:

|
Далее производят так называемую построчную проверку единичных перемещений. Она состоит в следующем. Находят сумму перемещений (δ 12 + δ 12). которую можно рассматривать как перемещение по направлению силы X1 , вызванное системой сил Х1=1 и Х2=1, действующих одновременно. Тогда
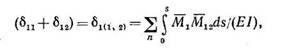 (10) (10)
|
где М12 — изгибающий момент от действия системы сил Х1=1 и X2= 1 по рис. 148,г.
Назовем момент М12 моментом в суммарном единичном состоянии. (В общем случае этот момент обозначают Ms)
Итак, сумма «единичных» перемещений первого канонического уравнения может быть получена путем перемножения единичной эпюры моментов на суммарную единичную эпюру моментов М12.
Аналогично,
 (11) (11)
|
— сумма единичных перемещений второго канонического уравнения получается перемножением эпюры М2 на эпюру М12.
Кроме построчной проверки, проводим универсальную проверку всех выражений (10) и (11), применяя теорему о взаимности перемещений для групповых и простых перемещений при наличии единичных силовых воздействий:

|
«Перемножая эпюру» М12 на нее же, получаем сумму всех единичных перемещений. Для нашего примера (рис. 148, г)

|
а сумма всех единичных перемещений

|
-универсальная проверка соблюдается.
Проведем еще первую построчную проверку:
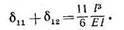
|
С другой стороны, перемножая эпюры М1 и М12, находим:

|
Таким образом, построчная проверка также выполняется. Кроме универсальной и построчной проверок проводим постолбцовую проверку грузовых членов Δ1p и Δ 2p к которой приходим на основании следующих равенств:

|
т. е. сумму всех грузовых членов получаем «перемножением» эпюры моментов от нагрузки Мр на эпюру моментов М12 (рис. 148, a, г).
В данном случае

— постолбцовая проверка выполняется.
Проверив правильность всех предшествующих вычислений, перейдем к решению уравнений. В данном случае, подставляя численные значения перемещений в канонические уравнения (5) и умножая все члены на EI, находим:
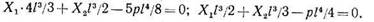
Решая уравнения способом исключения неизвестных, получаем:
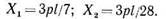
Проверка суммарной эпюры моментов. Применяя принцип сложения, получаем все ординаты «суммарной» эпюры моментов (рис. 148, д). При этом суммирование ординат эпюр Мр, Х1М1, Х2М2 проводим последовательно, вычисляя их для сечений, взятых по концам каждого стержня рамы и соединяя концы ординат соответствующими линиями (при отсутствии нагрузки — прямыми). Получив суммарную (окончательную) эпюру моментов, проводим проверку правильности ее построения. Для этого выясняем, выполняется ли каждое условие совместности перемещений вида (2), т. е.
 (12)
(12)
Вместе с тем перемещения по направлениям Х1 и Х2 от одновременного действия нагрузки и неизвестных Х1, Х2 можно найти, перемножая суммарную эпюру Mсум на соответствующую единичную эпюру моментов М1 или M2. Вместо выражения (12) получим:
 (13)
(13)
Результат перемножения суммарной эпюры моментов на любую единичную должен равняться нулю. Заметим, что это соотношение не выполняется при действии на статически неопределимую систему температуры.
В частном случае, если Mt — const вдоль всех стержней рамы и рассматривается случай действия нагрузки, вместо выражения (13) получим
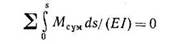
— приведенная площадь эпюры моментов [площадь Mсум / (EI)], подсчитанная по всей длине оси рамы, должна быть равна нулю, если для какого-либо состояния Хi=1 эпюра Мi- постоянна (например, в случае замкнутого бесшарнирного контура).