Найдём точечные и интервальные оценки генеральной средней и генерального среднего квадратического отклонения.

Представленную в табл. 1 совокупность можно считать выборкой из генеральной совокупности, то есть совокупности всех изучаемых объектов. По этим данным можно найти такое количественное значение признака, которое позволяет получить и надёжное представление об интересующем нас параметре, то есть получить статистическую оценку. Различают оценки точечные и интервальные.

Точечной называют статистическую оценку, которая определяется одним числом. Для генеральной средней точечной оценкой является выборочная средняя, т.е. ; для генерального среднего квадратического отклонения такой оценкой является выборочное среднее квадратическое отклонение, т.е. 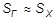. При этом следует помнить, что при небольших объёмах выборки (n < 60) следует умножить S_Х на корректирующий множитель .

Таким образом, для нашей задачи точечная оценка генеральной средней – это выборочная средняя, то есть, .Точечной оценкой генерального среднего квадратического отклонения будет величина: S_Г ≈S_Х ≈ 11,9.

Интервальной называют оценку, которая определяется двумя числами ─ концами интервала, покрывающего оцениваемый параметр.

Интервальную оценку генеральной средней a нормальной совокупности можно найти по формуле: , где t = t(p,n) – аргумент функции Лапласа, при котором Ф(t) = p. Значение t находят по таблице приложения 5.

Интервальной оценкой генерального среднего квадратического отклонения S_Г нормально распределённого признака Х служит доверительный интервал:

при q < 1,

0 < S_Г < S_Х (1+q) при q>1,

где q=q(p;n) находят по таблице приложения 6.

Для определения интервальной оценки генеральной средней а по заданным p = 0,95 и n = 60 из таблицы приложения 5 найдём t = t(0,95;60) = 2. Теперь рассчитаем предельную оценку выборки и доверительный интервал для генеральной средней из неравенства:

Тогда 45,5 – 3,2 < а <45,5 + 3,2 или 42,3 < a < 48,7.

Интервальные оценки генерального среднего квадратического отклонения S_Г вычисляются следующим образом. По таблице приложения 6 найдём q = q(p;n) = q(0,95;60) = 0,188.

Тогда из неравенства имеем:

11,9(1-0,188) < S_Г < 11,9(1+0,188)

или 9,7 < S_Г < 14,1.

6) Найдём теперь ошибки выборочных оценок. Ошибка выборочной средней (стандартное отклонение выборочной средней) при нормальном законе распределения определяется по формуле: .

Относительная ошибка выборочного среднего находится следующим образом:

Сопоставление ошибки выборочного среднего с его величиной даёт представление о точности вычисления выборочного среднего (точности опыта). Для рассматриваемой задачи ошибка выборочной средней равна . Относительная ошибка выборочного среднего (точность опыта): .

Ошибка выборочного среднего квадратического отклонения (стандарта) S_ст при нормальном законе распределения вычисляют по формуле: . Тогда относительная ошибка вычисления стандарта равна: . Ошибка выборочного среднего квадратического отклонения . Относительная ошибка вычисления стандарта: .

7) Проведем анализ вычисленных статистических параметров.

Полученные статистические характеристики дают возможность сделать следующие выводы:

- Затраты на животноводство по выбранным хозяйствам в среднем составляют 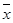= 455 тыс. руб. на 100 голов. В большинстве хозяйств они несколько больше: М₀ = 464 тыс. руб. При этом передовые хозяйства затрачивают на животноводство 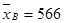тыс. руб., а отстающие ─ в среднем только по тыс. руб. Наиболее отстающими являются 10 хозяйств, у которых затраты не превышают 369 тыс. руб.

- Проведённая проверка согласия опытного и теоретического распределения по критериям χ² ─ Пирсона и ─ Смирнова подтвердила, что данный признак Х можно считать подчиняющимся закону нормального распределения. Это даёт основание при вычислении интервальных оценок параметров использовать формулы нормального распределения.

- Рассеяние данных относительно выборочного среднего характеризуется стандартным отклонением S_x =119 тыс. руб. коэффициент вариации V% = 26,2% превосходит 20 %, что свидетельствует о значительном разбросе данных выборки Х - денежных затрат на животноводство в различных хозяйствах.

- Вычисленная ошибка выборочного среднего тыс. руб. даёт возможность определить относительную ошибку найденного выборочного среднего , которая достаточно мала (менее 5%), а также найти при точность оценки генеральной средней (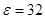тыс. руб.) и установить с надёжностью р = 0,95 доверительный интервал генеральной средней 423 < a < 487 тыс. руб., следовательно, можно с надёжностью р = 95% ожидать, что средние затраты на животноводство в целом по области (генеральная совокупность) будут находиться в пределах от 423 тыс. руб. до 487 тыс. руб. на 100 голов, а среднее квадратическое отклонение генеральной совокупности ─ в доверительном интервале: 97 < S_Г < 141 тыс. руб.