Доповняльний код числа

Доповняльний код числа N=-0,a₁a₂..a_n - таке машинне уявлення, в якому число записується оберненим кодом із збільшенням в молодшому розряді на +1.

Правило перекладу з прямого коду в додатній код наступне:

- якщо в знаковому розряді знаходиться (q-1) - тобто число негативне, то всі цифри числа, окрім розрядів знаків, замінюються вирахуваннями з (q-1) значення розряду, а потім до цифри останнього молодшого розряду додається одиниця;

-якщо в знаковому розряді знаходиться 0 (або 00) - тобто число позитивне, то перетворення цифр не відбувається.

 

Приклади:

а) -243476₍₁₀₎; 9243476_(10)пр = 9756523_об + 0000001 = 9756524_(10)доп

б) -0111000111₍₂₎; 1111000111_(2)пр.; 11000111000_(2)об + 0000000001₍₂₎= 11000111001_(2)доп

Перевірка:

11000111001_доп

+1111000111_пр

10.0000000000 (2₍₁₀₎)

в) –0,101110 ; 1101110_пр ; 110001_об + 000001 = 110010_доп.

г) +425736₍₁₀₎ ; 0425736_(10)пр = 0425736_(10)доп= 0425736_(10)об

Таким чином, для позитивних чисел прямий, оберненій і доповняльний коди співпадають, для негативного числа вони різні. Для позитивного числа в розряді знаку завжди встановлюють 0 або 00, а для негативного 1 або 11 (для довільної основи q знак «-» має код (q - 1)).

Узагальнемо і отримуємо вираз перекладу чисел у доповняльний код:

Приклади:

а) +0,275936₍₁₀₎; 0,275936_{(10) пр}= 0,275936_(10)доп (бо позитивне).

б) -0,275936₍₁₀₎; 10,000000₍₁₀₎+(–0,275936₍₁₀₎) = 9,724064_доп

Звідси N_доп=q+(-N), тобто додатній код є математичним доповненням числа до основи системи числення.

Покажемо, що доповняльний код – це доповнення до q, тобто: . Звідси, враховуючи це, будемо віднімати.

Приклад:

A = –0,1011; тоді A_доп = _ 10,0000

0,1011

1,0101 Отримано доповняльний код.

Покажемо, що обернений код – це доповнення до q–q^{- n}, тобто:

, якщо A негативне, то A_об=q–q^-n-|A|. Звідси, треба віднімати з q негативне число і молодшу 1 (тобто q^-n).

Для довільної основи q це означає, що обернений код числа А_об порозрядно формується від`ємом значення А_пр в і-му розряді від (q-1).

Максимальне додатне число, що представляється при цьому дорівнює (1–2^-n), або N_max = - 0,111...11 тоді додатній код буде N_дод =10... 01. Якщо в наймолодший розряд числа N_max додати 1 то отримаємо: -1,000...00. Перетворивши це число в додатній код, отримаємо,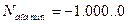тобто: –1 £ N_дод £ (1-2^-n).

 

7.4 Складання чисел, представлених у формі з фіксованою комою, на двійковому суматорі прямого коду

Двійковим суматором прямого коду (ДСПК) є суматор, в якому відсутній ланцюг порозрядного перенесення між старшим цифровим і знаковим розрядами (рис. 7.3).

Рисунок 7.3 - Двійковий суматор прямого коду (ДСПК)

На ДСПК можна складати тільки числа, що мають однакові знаки, а результат складання < 1 (для правильних дробів) або менше виразу 2ⁿ-1 (для цілого числа). Аналіз показує, що такий суматор виконує не всі операції складання, а лише дві з чотирьох: А+В і -(А+В). Сигнал пере-повнення П_n старшого n-розряду служить лише для індикації факту, що воно було, покладаючи подальші турботи на користувача або ЦА, а знак суми C визначається за знаком будь-якого операнда, наприклад Sg_A (Sg_B).

Нехай задані операнди:

де Sg_A і Sg_B – вміст знакових розрядів. Якщо Sg_A=Sg_B , то сума чисел матиме знак будь-якого з доданків, а цифрова її частина вийде порозрядним складанням операндів.

Приклади.

а) Скласти А = 01011 (+11); В = 0,0100 (+4). Тут Sg_A=0; Sg_B=0

+1011 (+11)

0100 (+4) С = 01111

01111 (+15)

б) Скласти A =-0101 (-5); B =-01001 (-9). Тут Sg_A=1; Sg_B=1

+0101 (-5)

1001 (-9) C = 11110

11110 (-14)

При складанні чисел на ДСПК можливі випадки, коли абсолютне значення суми операндів перевищує одиницю, тобто має місце переповнення розрядної сітки ЦА. Ознакою переповнення (g=1) буде наявність одиниці перенесення П_n із старшого розряду цифрової частини суматора. За цим сигналом повинні відбуватися автоматичний «останов» процесу рахування і коректування масштабних коефіцієнтів операндів А і В з розрахунком, щоб уникнути переповнення (наприклад зміна К_ф).

8 АЛГЕБРАЇЧНЕ СКЛАДАННЯ БІНАРНИХ ЧИСЕЛ

 

8.1 Складання чисел на двійковому суматорі доповняльного коду

Двійковим суматором доповняльного коду (ДСДК) називається суматор, що оперує числами, що представлені в доповняльному коді.

Основною особливістю ДСДК є наявність ланцюга перенесення одиниці переповнення П_n зі старшого розряду цифрової частини в знаковий розряд (рис. 8.1) і відсутність зворотнього зв’язку перенесення одиниці переповненняП_Sg із знакового розряду в наймолодший розряд числа.

Рисунок 8.1 -Двійковий суматор доповняльного коду (ДСДК)

Для визначення правил складання чисел в ДСДК розглянемо наступну теорему: якщо результат суми доповняльних кодів чисел негативний, то він представлений у доповняльному коді.

При доведенні теореми, припускаємо, що числа представлені у формі з фіксованою комою, що стоїть перед старшим розрядом. Розглянемо наступні випадки (всі числа є цілими):

Випадок 1. A>0, B>0, а A+B<1 числа позитивні і немає переповнення. Для цього випадку A_доп =А, В_доп=В, то А_доп+В_доп=А+В=[A+B]_доп - результат позитивний. Покажемо це на прикладі: А = +0,1010; В = +0,0100.

С=+0,1110.

Випадок 2. A<0, B>0, а |A|>B. Для цього випадку А_доп=q+|-A |, В_доп=В; тоді А_доп+В_доп=q+|A|+B=[A+B]_доп – результат негативний.

А=-0,1011; В=+0,0100

С= - 0,0111.

Отриманий результат негативний, це означає, що він представлений у доповняльному коді, і його необхідно перевести в прямий, щоб отримати дійсний результат. Переклад числа з доповняльного коду в прямий здійснюємо за наступним алгоритмом: усі розряди числа (окрім знакових) інвертуються (тобто береться обернений код результату) і в молодший розряд додається 1. Знак суми С зберігається.

Випадок 3. A<0, B>0, а |A|<B. для цього випадку А_доп=q+|A|, В_доп=В; тоді А_доп+В_доп=q+|A|+B. Оскільки значення цієї суми більше q, то з’являється одиниця перенесення в знаковий розряд, що дорівнює вилученню з суми q одиниці, тобто результат:А_доп+В_доп=А+В=С_пр.

Приклад. А =-0,0100; В =+0,1011.

С= + 0,0111.

Випадок 4. A<0, B<0, а |A+B|<1. Для цього випадку А_доп=q+(-А); В_доп= q+(-В), тоді А_доп+В_доп=q+(-A)+q+(-B)=[A+B]_доп - результат негативний і з’явиться одиниця перенесення із знакового розряду.

Приклад. А = -0,0100; В = -0,1011.

С_пр=1,1111. С= -0,1111

Висновок. Теорема справедлива для всіх випадків, в яких не виникає переповнення розрядної сітки, що дозволяє складати в ДСДК машинні зображення чисел за правилами двійкової арифметики. Приклади:

Випадок 1. A>0, B>0, C<1.

а) A₍₁₀₎ = +0,372914_(10)пр; В₍₁₀₎ = +0,564019_пр

 

 

б) Для цілих чисел: А_пр= 01001110101 (+629) В_пр=0101110011(+371)

 

Перевірка: 629+371=1000

Випадок 2. A>0, B>0, C³1 (переповнення розрядової сітки):

П

 

 

оПоява в знаковому розряді одиниці позитивного переповнення говорить про переривання роботи для зміни K_Ф або зсув мантиси вправо на один розряд, а до порядку результату додається одиниця (тобто проводиться нормалізація результату).

Апр = 01101110101 Впр = 0101110011 Адоп = 01101110101 + Вдоп = 0101110011 Сдоп = 1011101000 (далі зсув вправо на один розряд) Спр = 010011101000.

 

Перевірка: +885 + 371 =1256

Відбулося переповнення (g=1), тобто в знаковому розряді Sg_С0 з’явилася ознака (1). Що це? ЦА не може розібрати ситуацію, це знак «мінус» суми С або ознака переповнення. Для вирішення цього треба в поле знаків додати ще один розряд (використовується модифікований доповняльний код, див. гл. 9).

Зсув вправо (вліво) числа зменшує (збільшує) його на порядок: тобто змінеться К_ф (для ФФК) або порядок Р (для ФРК) і цю зміну треба відкорегувати, щоб значення числа не змінилось.

Випадок 3. A>0, B<0, |A|>|B|: тобто C =A+q+B оскільки C>q, то q повинне бути відібране, що робиться шляхом відкидання сигналу перенесення, що виникає в знаковому розряді.

	A(10)пр=+0.732904; В(10)пр= -0.042703(зрівняно кількість розрядів А і В), В(10)доп=9,957297 [А]доп = 0,732904 + [В]доп = 9,957297 [С]доп =10,690201; Спр = +0,690201. При цьому в ДСДК переповнення 1 розряду SgC не використовується (відкидається).

 

 

При визначенні доповняльного коду В_(10)доп, спочатку провели вирівнювання розрядності чисел, додавши 0 в старший розряд числа В_пр, а потім віднімали з (q-1)=9 значення по кожному розряду і отримали обернений код, потім до його молодшого розряду додали 1.

 

Розглянемо ще приклад:

А_(2)пр=01101110101 (+885); В_(2)пр =1110110101 (-437).

 

 

Одиниця переповнення 1 відкидається (бо ДСДК), знак результату С позитивний і означає прямий код.

Випадок 4. A>0, B<0, |A|<|B|, C =A+q+B, оскільки C<0, то C=q+(A+B).

Випадок 5. A<0, B<0, |A|+|B|<1, C=q+A+q+B<0. При цьому, одна основа повинна бути відкинута за рахунок втрати сигналу перенесення в знаковому розряді. Тоді C=q+(A+B).

Випадок 6. A<0, B<0, але |A|+|B|>0.

Це також випадок переповнення розрядної сітки, але на відміну від випадку 2 переповнення тут негативне.

A_(10)пр = -0,610892₍₁₀₎; В_(10)пр = -0,843507₍₁₀₎

А_доп = 9,389108

+ В_доп = 9,156493

С_доп =18,545601

Поява цифри 8 в знаковому розряді говорить про те, що відбулося переповнення Sg_С0, необхідний зсув вправо з відновленням знаку і перетворення результату в прямий код.

С_доп=18,545601; після зсуву С_доп=9,8545601 (проведено зсув на 1 розряд вправо і відновлення знаку), С_пр=9,1454399.

Розглянемо приклад в двійковій системі числення.

А_пр = -1101110100; В_пр = -1110111010

А_доп = 1010001100

+ В_доп = 1001000110

С_доп =10011010010

Було переповнення. Необхідний зсув вправо, для відновлення знаку з подальшим перетворенням результату в прямий код.

С_доп =10011010010=10011010010;

С_пр=111100101110. Перевірка: -884-954= -1838.

У звичайному доповняльному коді є проблема із зображенням числа «-1». Тут розглядають два варіанти:

1. Виробляти сигнал переповнення, якщо в знаковому розряді (q-1), а в цифрових розрядах є нулі тобто А_доп= 1.0000…0.

2. Вважати -1 допустимим значенням, але при цьому її зображення в прямому коді співпадатиме із зображенням у доповняльному коді.

-1_(10)доп = 9.00000…0 = 9.99999…9 + 0.0000…01 = 9.00000…0 = -1_(10)пр

-1_(2)доп = 1.00000…0 = 1.11111…1 + 0.0000…01 = -1_(2)пр

Щоб відрізняти -1 від +1, використовують модифікований доповняльнийкод (див. розділ 9).

 

8.2 Складання чисел на суматорі оберненого коду

Двійковим суматором оберненого коду (ДСОК) є суматор, що оперує з числами в оберненому коді.

Структурна схема ДСОК приведена на рис. 8.2.

Рисунок 8.2 - Двійковий суматор оберненого коду (ДСОК)

Основною особливістю ДСОК є наявність ланцюга перенесення одиниці переповнення П_n із старшого розряду цифрової частини в знаковий розряд (рис. 8.2) і наявність зворотнього зв’язку перенесення одиниці пере-повненняП_Sg із старшого знакового розряду Sg₁ в молодший розряд числа.

ДСОК має: n суматорів (по кількості розрядів мантиси); суматор знакових розрядів; a_i, b_i - цифрові розряди числа в машинному коді; перенесення із старших розрядів мантиси в знаковий розряд; нарешті, обернене перенесення із старшого знакового розряду в молодший розряд цифрової частини числа. Щоб сформувати правила складання чисел в обернених кодах на ДСОК розглянемо теорему.

Теорема: сума обернених кодів чисел є обернений код результату.

При доведенні цієї теореми припускаємо, що числа представлені у формі з фіксованою комою, що стоїть перед старшим цифровим розрядом.

Розглянемо наступні випадки складання на суматорі ДСОК.

Випадок 1. А>0, В>0, А+В<1 (тобто обидва числа позитивні).

Тоді А_об+В_об=[A +B]_об =А+В, тобто складання проводиться в прямих кодах.

Приклад: А = 0101 (+5)

В = 0111 (+7)

С = 01100 (+12)

Випадок 2. A<0, B>0, |A|>B, А_об=q-q^-n+A, В_об=В, тоді А_об+В_об=q-q^-n+A+B=[A+B]_об, тобто результат негативний і в оберненому коді, треба повертатися до С_пр шляхом інверсії розрядів числа.

Приклад: А = -01011 (-11), В = 0111 (+7).

А_об=1100

+В_об=0111

С_об=11011 С_пр=1100 (-4)

Випадок 3. A<0, B>0, A<B, тут А_об = q-q^-n+A. Тоді А_об+В_об=q-q^-n+A+B. Оскільки сума (А +В) позитивна, то права частина цього виразу стає більше q, що викликає появу одиниці перенесення із знакового розряду в молодший розряд числа (величина перенесення при цьому, рівна q-q^-n), тоді А_об+В_об=А+В. Результат позитивний, це і є С_пр.

Приклад: А = -0101 (-5); В = 0111 (+7).

А_об = 11010

+В_об = 0111

С_об = 10001

⁺ a→→1

С_пр=0010(+2). Оскільки В>|A|, то їх алгебраїчна різниця позитивна.

Випадок 4. А<0, В<О, |А + В|<1, тут A_об=q-q^-n+A, В_об=q-q^-n+B. Тоді А_об+В_об=q-q^-n+A+q-q^-n+B. Тут з’являється одиниця перенесення, що дорівнює вилученню з суми -q^-n, тобто А_об+В_об=q-q^-n+A+B=[A+B]_об

Приклад: А = -0,0101 ; В = -0,1000.

А_об=1,1010

+В_об=1,0111

11,0001

⁺ a→→1

С_об=1,0010; С_пр= 1,1101 (-0,8125).

9 МОДИФІКОВАНІ БІНАРНІ КОДИ

 

9.1 Переповнення розрядної сітки

Ми не раз спостерігали, як при складанні чисел з однаковими знаками, представлених у формі з фіксованою комою (ФФК), може виникнути переповнення розрядної сітки. При цьому, щоб уникнути спотворення резуль-тату, автомат повинен фіксувати переповнення і відповідно реагувати на це.

 

9.1.1 Переповнення при складанні прямих кодів

Ознакою переповнення розрядної сітки суматора прямого коду є поява одиниці перенесення із старшого розряду цифрової частини числа.

Приклади. Суматор ДСПК.

а) А=+1010, В=+1101.

А_пр= 01010 (+10)

+В_пр= 01101 (+13)

С_пр= 0111 (+7≠ +23). Отримано спотворений (невірний) результат із-за втрати перенесення П зі старшого цифрового розряду.

б) А=-1100, В= -1010.

А_пр= 11100

+В_пр= 11010

С_пр= 1110 (-6≠-22). Тут теж отриманий невірний результат із-за втрати одиниці перенесення.

 

9.1.2 Переповнення при складанні доповняльних кодів

Ознакою переповнення розрядної сітки суматора доповняльного коду при складанні позитивних чисел є негативний знак результату, а при складанні негативних чисел - позитивний знак результату.

Приклади:

а) А= +01011; В= +01010 (перевірку отриманого результату проведіть самостійно).

 

б) А= -01011; В= -01001 (перевірку отриманого результату проведіть самостійно).

 

 

9.1.3 Переповнення при складанні в обернених кодах

Ознакою переповнення розрядної сітки суматора оберненого коду є знак результату, протилежний знакам операндів.

Приклад:

1) А=0111; В=01101.

 

 

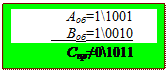Знак числа спотворений (невірний):

2) А= -0110; В= -01101.

 

 

Знак числа спотворений (невірний)

Для усунення втрат від неврахування перенесення одиниці та формування стану переповнення, у складі ЦА повинні бути перед-бачені додаткові засоби, що дозволяють фіксувати і аналізувати пере-повнення за їх ознаками з метою усунення спотворення результату.

Щоб фіксувати переповнення розрядної сітки в ДСПК, ДСДК, ДСОК, вводять допоміжний розряд в знакову частину зображення числа, який називають розрядом переповнення числа. Таке представлення числа називається модифікованим (див. рис. 9.1).

Рисунок 9.1 - Модифікований код числа для ФФК

Приклади:

а) [А]_пр=001100111011, тоді, оскільки А>0 маємо: [а]_М.доп=001100111011

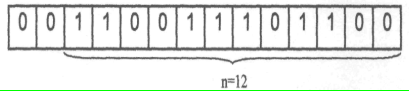
б) А_пр = -01100111011, оскільки А<0, то А_м.доп =100+(-A_пр)=q²-A

_100000000000

01100111011

11011000101

 

ПРАВИЛО: для переводу бінарного числа з прямого коду в модифіковний доповняльний код, аналізують знак числа. Якщо в знаковому розряді знаходиться мінус (одиниця), то в два знакових розряди записують одиниці, а всі цифри числа інвертують (одиниці заміняють нулями, а нулі - одиницями), потім до останньої молодшій цифрі (молодшого розряду) числа додають одиницю. Якщо в знаковому розряді стоїть нуль, то додають ще один, а число не змінюють. ПРАВИЛО: для переводу бінарного числа з прямого коду в модифіковний обернений код, аналізують знак числа. Якщо в знаковому розряді знаходиться мінус (одиниця), то в два знакових розряди записують одиниці, а всі цифри числа інвертують (одиниці заміняють нулями, а нулі - одиницями). Коли в знаковому розряді стоїть нуль, то додають ще один, а число не змінюють. При виконанні операцій алгебраїчного додавання або вирахування два знакових розряди приймають участь в операції, як рівноправні цифрові розряди. Після виконання операцій, стан знакових розрядів (знак результату) встановлює лівий знаковий розряд, а наявність чи відсутність переповнення - правий знаковий розряд. Знакові розряди можуть мати наступні комбінації станів при будь- яких значеннях операндів А і В: - 00 - результат числа позитивний, переповнення немає; - 01 - результат числа позитивний, було переповнення; - 11 - результат числа негативний, переповнення немає; - 10 - результат числа негативний , було переповнення.

 

У машинному представленні чисел, представлених в модифіко-ваному коді, використовується (n+2) розрядів: з них два знакових, кома опускається, встановлюється постійний коефіцієнт формату К_ф. Сигнал переповнення g виробляється по наступній математичній моделі (тут знак Ù позначає логічну операцію множення «і», а риска над символом Sg – логічну операцію інверсії

γ = 1, якщо Sg1 Ù`Sg2= 1

` Sg1 Ù Sg2= 1,і γ = 0в інших випадках.

Приклади: а) А= 01011 (+11), В= 01010 (+10).

 

 

Тут ознакою переповнення є 1 в знаковому розряді. За цією ознакою проводиться зрушення числа вправо з одночасним збільшенням коефіцієнта формату К_ф на 1 і відновленням Sg₁ (по значенню Sg₂)обох розрядів Sg₁Sg₂, тобто знаку 00 результату С числа, далі перевіряється нормалізація числа (наявність 1 після коми в числі).

б) А= -01011 (-11), В= -01001(-9). Перетворимо в машинну форму: А^м_пр=111011, В^м_пр=111001. Оскільки обидва числа негативні і операція складання виконується на ДСДК, то в суматор числа поступають в доповняльному коді.

Аналіз розрядів знаку результату (10 - див. третю строку) показав, необхідність відновлення його (до 11), зрушуючи число вправо на один розряд, з одночасним збільшенням коефіцієнта формату К_ф на 1. Результат негативний, і тому представлений у доповняльному коді. Тому результат перетвориться в істиний (прямий код) через інвертування (обернений код) і з додаванням +1 в молодший розряд.

9.2 Модифіковане складання чисел у форматі з рухомою крапкою (комою)

Числа, представлені у форматі з рухомою крапкою (комою) – ФРК, мають дві часті: мантису і порядок. Тому, операція додавання (складання) виконується окремо над мантисою і над порядком. Отже, в ЦА може бути два суматори: для мантиси і для порядку.

Для чисел з рухомою крапкою справедлива умова нормалізації:

q^-1≤|m_A| < 1, (9.1)

де q - основа системи числення; m_A - мантиси числа.

Це нормалізоване представлення числа, яке вимагає, щоб в старшому розряді мантиси 2-го числа була одиниця. Для двійкової системи це означатиме, що мантиса завжди знаходиться в межах:

0,5≤|m_A|<1, (9.2)

При виконанні автоматом операцій над числами, нормалізують як вхідні доданки А і В, так і вихідний результат С.

Операція нормалізації числа складається з умови нормалізації (9.1) і здійснюється методом зрушення мантиси числа в ту або іншу сторону.

Зрушення можуть проводитися вліво або управо в межах розрядної сітки ЦА за правилами представлених моделлю таблиці 9.1.

Таблиця 9.1 -Зсув звичайних кодів числа (один розряд знаку)

Початкове число	Зсув вліво на один розряд (від порядку вираховується 1)	Зсув вправо на один розряд (до порядку додається 1)
0/a1 a2... an 1/a1 a2... a n	a1/a 2... a n 0 a1/a2... a ne	0/0 a1 a2... an 0/1 a1 a2... an

Величина e залежить від коду. Для доповняльного коду ε=0, для оберненого коду e=1. При складанні чисел результат може вийти з нормалізації як зліва, так і справа (див. табл. 9.1, 9.2).

Ознакою порушення нормалізації числа справа γ=1 (коли результат має переповнення) є наявність різнойменних комбінацій в знакових розрядах сумматора:

γ=1, якщо Sg1 Ù`Sg2= 1

`Sg1 Ù Sg2= 1, і γ=0 у решті випадків.

Таблиця 9.2 -Зсув модифікованих кодів числа (два розряди знаку)

Початкове число	Зсув вліво на один розряд (від порядку вираховується 1)	Зсув вправо на один розряд (до порядку додається 1)
00/α1,α2,...,αn 01/α1,α2,...,αn 10/α1,α2,...,αn 11/α1,α2,...,αn	0α1/α2,...,αn 0 1α1/α2,...,αn 0 0α1/α2,...,αn ε 1α1/α2,...,αnε	00/0,α1,α2,...,αn 00/1,α1,α2,...,αn 11/0,α1,α2,...,αn 11/1,α1,α2,...,αn

(де γ - ознака порушення нормалізації числа справа, вказує на необхідність зсуву числа вправо на один розряд для відновлення знаку числа).

Ознакою порушення нормалізації числа зліва δ=1 (коли результат по абсолютній величині виявляється менше 1/q ) є наявність однакових комбінацій в розряді переповнення і старшому розряді (R1) цифрової частини суматора:

δ=1, якщо Sg2 Ù R1 = 1

`Sg2 Ù`R1 = 1, іδ=0 у решті випадків,

(де δ – ознака порушення нормалізації, що вказує на необхідність зсуву числа вліво на один розряд). Зазвичай Sg1 (або Sg0)- старший, а Sg2 (або Sg1)- молодший знакові розряди.

Таким чином, операція нормалізації отриманого числа (суми двох операндів) складатиметься з сукупності перевірки наявності ознак порушення γ і δ та зсувів (вправо, вліво) числа.

Отже, розглянемо складання чисел А=m_Ap_A и В=m_Bp_B, що мають однаковий порядок p_A=p_B. Обидві мантиси задовольняють умові нормалізації. Складання мантиси здійснюють на суматорі ДСДК або ДСОК за правилом складання чисел представлених у формі з фіксованою комою. Якщо після складання мантиса результату задовольняє умові нормалізації (тобто δ=0, γ=0), то до цього результату приписується порядок будь-якого з операндів. Інакше відбувається нормалізація числа.

Приклад 1. Знайти суму чисел: А=0,1000×2^-3 та В=-0,1011×2^-3.

Мантиси і порядок обробляються на ДСДК у ФРК.

[m_А]_д=00/,1000 [Р_А]_д=11/101

+[m_B]_д=11/,0101 [Рв]_д=11/101

[m_с]_д=11/,1101

Тут Sg2&R1=1, тобто δ=1, γ=0. Це означає, що необхідний зсув мантиси [m_с]_д вліво на 1 розряд.

[m’_c]=11/,1010 Перевіряємо. Знову δ=1, γ=0 - необхідний ще зсув вліво на 1 розряд.

[m’’_c]_д= 11/,0100. Перевіряємо, все гаразд δ=0, γ=0.

Одночасно зі зрушенням потрібна корекція порядку на мінус 2₍₁₀₎=11/010_(2). (що рівнозначно збільшенню порядку на дві одиниці – у доповняльному коді 11/110).

₊[Р_с]_д=11/101

[ΔP_c]_д=11/110 [ΔР_с]_пр=11/010

[Р’’_с]_д=11/011 Р_{С пр}=-11/101 (тобто Р= 2^-5)

тоді результат (число) дорівнює:

[m’’_c]_д= 11/,0100

[m’’_c]_об=11/,1011

+ 1

11/,1100.

Відповідь: m_{C пр}=11/,1100. З урахуванням порядку запис для 16-ти розрядної ЕОМ С_пр= 11/,11000000/11/0101/.

Приклад 2. Знайти суму чисел А=-0,1100×2⁴ та В=-0,1000×2⁴. Мантиси і порядок обробляються на ДСОК у ФРК (шість розрядів мантиси і чотири для порядку). Порядки [P_A]=[P_B]=[P_C]_об= 0,100 (оскільки позитивні і рівні обидва порядки операндів А і В).

 

₊[m_А]_об=11/,0011

[m_B]_об=11/,0111

[m_C]_об=110/,1010

+ a→ → 1

10/,1011 (δ=0, γ=1)

Порушення нормалізації справа (тобто γ=1 означає, що було переповнення). Число зсуваємо вправо на один розряд, відновлюючи знак 11 і одночасно збільшуючи порядок Р на 1.

Тобто [m_C]_об=11/,0101, тепер δ=0, γ=0. Одночасно коректуємо і порядок:

₊[Рс]= 00/100

[ΔPс]=00/001

00/101 (+5), тоді відповідь: -0,1010×2⁺⁵ (Самостійно зробіть запис С_пр для 16-ти розрядної ЕОМ).

10 СКЛАДАННЯ ЧИСЕЛ ПРИ РІЗНИХ ЗНАЧЕННЯХ ПОРЯДКІВ

Для операції складання чисел необхідною умовою є зіставлення вагів розрядів операндів один одному. Тому спочатку потрібно вирівняти порядки, що спричинить за собою тимчасове порушення нормалізації одного з доданків (А або В).

Вирівнювання порядків означає, що порядок меншого числа треба збільшити на величину ΔР=р_а-р_в , що означає зсув мантиси меншого числа вправо на кількість розрядів, рівне р_а≥р_в. Тому, цифровий автомат повинен спочатку розпізнати, який порядок з двох чисел є меншим. На це вкаже знак ΔР. Якщо р_а≥р_в - знак позитивний і навпаки, якщо знак негативний, то Р_А < Р_В. Цю операцію іноді виконують шляхом порівняння чисел.

10.1 Алгоритм операції складання у форматі з рухомою крапкою (комою)

Отже, операція складання (віднімання) виконується в наступній послідовності.

1. Перевести операнди в двійкові доповняльні (або обернені) модифіковані коди, перевіривши перед цим нормалізацію початкових чисел.

2. Визначити різницю порядків ΔР = р_а-р_в

3. Якщо ΔР>0, зсунути мантису числа В на ΔР розрядів вправо; якщо ΔР<0, зсунути мантису числа А на ΔР розрядів вправо; якщо ΔР=0, мантиси не зсуваються (розряди виходять за межі розрядної сітки мантиси втрачаються).

4. Виконати операцію алгебраїчного складання (віднімання) над мантисами. Алгебраїчне складання виконується за наступним правилом. Аналізується знак числа:

- якщо знак позитивний (00), то в суматор мантиси число поступає в прямому коді;

- якщо знак негативний (11), то в суматор мантиси число поступає в доповняльному (оберненому) коді;

Складання проводиться порозрядно, за правилами бінарної арифметики, з перенесенням одиниці переповнення в старший розряд. Знакові розряди також беруть участь в складанні. Одиниця переповнення в старшому знаковому розряді для суматорів доповняльного коду пропадає, для суматорів оберненого коду по оберненому зв’язку додається до молодшого розряду мантиси.

До представлення результату в прямому коді, після складання, аналізується знак результату:

- якщо знак 01(або 10), то знак спочатку відновлюється шляхом зсуву мантиси вправо на один розряд з одночасним збільшенням порядку на 1;

- якщо знак 00, то результат- число позитивне, представлено в прямому коді;

- якщо знак 11, то результат- число негативне і представлено в оберненому (доповняльному) коді.

В цьому випадку, потрібне перетворення числа із оберненого (доповняльного) в прямий код, шляхом інвертування числа (окрім знаку) для ДСОК і інвертування числа (окрім знаку) з додаванням 1 до молодшого розряду мантиси для ДСДК. Результату встановлюється порядок більшого за модулем числа.

5. Проводиться перевірка числа на нормалізацію (для нормалізованих чисел, після знаку мантиси повинна стояти одиниця). Якщо після знаку мантиси стоїть нуль, то число зсувається вліво на один розряд (з одночасним зменшенням порядку на 1). Перевіряється нормалізація (перевіряємо ознаки порушення γ і δ). Цикл може повторюватися до досягнення умов нормалізації γ=0 і δ=0). За цим алгоритмом виконують операції складання і віднімання АЛП.

Приклад. Скласти А=+0,1011×2^-2 и В = -0,1001×2^-3

Числа задані в природному вигляді. В АЛП використовується два суматори оберненого коду: суматор мантис (шість розрядів, включаючи знак); суматор порядків (разом із знаком - чотири розряди).

РІШЕННЯ.

1. Враховуючи, що числа задані вже в нормалізованому вигляді (після коми стоїть 1), представимо їх в машинному вигляді у форматі з рухомою крапкою (модифікований код): А^м_пр=00.1011.11.10; В^м_пр=11.1001.11.11.

2. Переводимо мантиси чисел в обернені коди: m_Аоб=00.1011; m_Воб=11.0110.

3. Для вирівнювання порядків чисел, а значить, і їх вагових розрядів, необхідно з’ясувати, яке із заданих чисел підлягає тимчасовій денормалізації. Для цього автоматом визначається різниця порядків чисел: DР=Р_А–Р_В. Переведемо порядки чисел в обернені коди.

Р_Аоб=11.01 ; Р_Воб=11.00. Тоді, DР=Р_Аоб-Р_Воб =11.01–11.00

Замінимо операцію віднімання на операцію складання.

DР=Р_Аоб-Р_Воб = Р_Аоб +`Р_Впр =11.01 + 00.11 (де Р_Впр - інверсний код Р_Воб., включаючи і знакову частину).

 

Виконаємо додавання.

11.01

+00.11

100.00

+a→1

00.01

Величина DР позитивна, тому Р_А > Р_В. Треба зсувати мантису числа вправо на DР розрядів, тобто на один розряд, збільшивши одночасно порядок на 1.

4. Зсунемо мантису числа В вправо на один розряд і складемо їх значення на ДСОК.

5. Перевіримо умову нормалізації мантиси результату справа, зліва.

 

mАоб=00.1011 (тут δ=0, γ=0) mBоб=11.0110 (тут δ=0, γ=1, необхідно зробити зсув mBоб вправо) mBоб=11.1011 +mAоб=00.1011 mCоб=100.0110 a→→ 1 00.0111 (тут δ=1, γ=0; необхідно зробити зсув вліво) mCоб=00.1110 і тому робимо корекцію порядку на ∆Р=–1 РАоб=11.01 +∆Роб= 11.10 (∆Р представлено в оберненому коді) 110.11 +a→1 РСоб=11.00 Результат РСоб отриманий в оберненому коді, тобто знак негативний (11). Визначаємо прямий код порядку і записуємо результат Спр=00.1110×2-3. Відповідь: Спр=00.1110.11.11

 

Приклад. Скласти на ДСДК числа А_пр= +5, В_пр= -3, представлених в десятковій системі числення. А_д=00/5; В_д=99/7. Проведемо складання А_д+В_д=00/5+99/7=100/2=00/2 (+2₍₁₀₎). Одиниця (1) пропадає, оскільки складання йде на ДСДК.

 

 

11 МНОЖЕННЯ ДВІЙКОВИХ ЧИСЕЛ

 

11.1 Методи множення бінарних чисел

Розглянемо основні способи виконання операції множення для різних систем. Найпоширенішим способом множення чисел є спосіб порозрядного множення множеного на множник, починаючи з молодшого розряду (1-й спосіб), починаючи зі старшого розряду (2-й спосіб). Розглянемо приклад:

 

Аналіз способів множення чисел в десятковій системі показує, що операція множення складається з порозрядного множення множеного на множник з перенесенням переповнення в старший розряд, зрушення часткових добутків на один розряд вліво (вправо), підсумовування часткових добутків.

У двійковому численні це завдання значно спрощується, оскільки множити порозрядно немає необхідності. Насправді, якщо множити множене на "1", то це повторення множеного із зсувом на один розряд вправо (вліво), а на "0" - записуються одні нулі із зрушенням.

 

 

 

 

В обох випадках операція множення складається з ряду послідовних операцій зсуву і складання часткових добутків. Таким чином, операція множення зводиться до складання часткових добутків, які виходять з множеного або нулів, якщо в розряді множника «нуль», або множеного, якщо в розряді множника «одиниця» і відповідним або зсувом.

Окрім операції складання, при виконанні множення, з’являється операція зсуву чисел. При цьому, можливі два варіанти:

- зсувати множене відповідно до вказівок множника;

- зсувати суму часткових добутків.

Розглянемо основні методи виконання операції множення ЦА.

МЕТОД 1. Нехай А - множене > 0, В - множник > 0, а С - добуток.

Запишемо числа у ФФК: A=0,α₁α_2,...,α_n; B=0,b₁,b₂,...,b_n (А і В правильні дроби). В - множник і він визначає розрядність С (чим він більший, тим більша розрядність С). Тоді, B=b₁×2^-1+b₂×2^-2+...+b_n×2^-n.

Звідси: C=A×B = 0,α₁α_2... α_n(b₁×2^-1+b₂×2^-2+.. .+b_n×2^-n)=

=(2^-1×0,α₁α_2... α_n)b_l+(2^-2×0,α₁α_2... α_n)b₂+...+(2^-n×0,α₁α_2... α_n)b_n.. (11.1)

Множник 2^-n означає зсув на n розрядів вправо числа, що укладено в дужки, тобто зсуваэться вправо множене і множення на множник починається зі старших розрядів. Структурно це зображено на рис. 11.1.

Рисунок 11.1 - Метод множення зі зрушенням вправо множеного

МЕТОД 2. Нехай A=0,α₁α_2... α_n - множене; B=0,b_lb₂...b_n - множник. Перетворимо множник по методу Горнера:

B=(...((b_n×2^-1+b_n-1)×2^-1+b_n-2)×2^-1+...+b₂)×2^-1+b₁)×2^-1.

Тоді,

C=A×B=(...(b_n×0,α₁α_2...α_n)×2^-1+b_n-1×0,α₁α_2...α_n)×2¹+...+b₁×0,α₁α_2...α_n)2^-1, (11.2)

За цією моделлю, множення починається з молодших розрядів і вправо зрушується. Структура наведена на рис. 11.2

Рисунок 11.2 - Метод множення зі зрушенням вправо суми часткових добутків

МЕТОД 3. Нехай A=0,α₁α_2...α_n - множене; B=0,b_lb₂...b_n – множник. Використовуючи метод Горнера, запишемо множник:

B=2^-n(b₁×2n^-1+b₂×2^n-2+...+b_n-1×2¹+b_n×2⁰). Тоді,C=A×B=

=2^-n(b_n×0,α₁α_2...α_n+(2¹×0,α₁α_2...α_n)×b_n-1+...+(2^n-1×0,α₁α_2...α_n)×b₁ (11.3)

 

Це означає: множення починається з молодших розрядів і множене зсувається вліво на один розряд у циклі. Структура представлена на рис.11.3.

Рисунок 11.3 - Метод множення зі зрушенням вліво множеного на один розряд у циклі

МЕТОД 4.Нехай A=0,α₁α_2...α_n - множене; B=0,b_lb₂...b_n – множник. Запишемо В - множник по методу Горнера, як у попередньому методі. Тоді, C=A×B=

=2^-n(...(2¹(b₁×0,α₁α_2...α_n)+b₂×0,α₁α_2...α_n)2¹+…

+b_n1×0,α₁α_2...α_n)2¹+ +b_n×0,α₁α_2...α_n). (11.4)

За цією моделлю множення починається зі старшого розряду і в кожному циклі сума часткових добутків зрушується вліво. Схема такого множного пристрою наведена на рис.11.4.

Рисунок 11.4 - Метод множення зі зрушенням вліво суми часткових добутків

Таким чином, для реалізації операції множення необхідно мати, як мінімум: суматор, регістри для зберігання множеного й множника, схему аналізу розрядів множника. Суматор і регістри повинні мати ланцюги зсуву вмісту в ту або іншу сторону відповідно до прийнятого методу множення.

 

11.2 Множення чисел з фіксованою крапкою (комою) на ДСПК

Запишемо машинне зображення множеного і множника у формі з фіксованою комою в прямому коді. A_np=Sg,α₁α_2...α_n; B_пр=Sg,b₁b₂...b_n. Тоді, їхній добуток запишеться як C_np=Sg,с₁с₂...с_n, де Sg_С=Sg_АÅSg_В, де Å - знак додавання функції «Σ по mod2» ( її ТІ: 1Å1=0, 0Å0=0, 1Å0=1, 0Å1=1).

Таким чином, при використанні ДСПК, знак добутку визначається окремо від цифрової частини, потім виконується операція множення. Вона виконується відповідно до заданої структури множного пристрою (див. наприклад, рис. 11.5) і методу множення (див. наприклад, метод 2).

За методом 2 множення починається з молодшого розряду і зсувається вправо сума (Σ) часткових добутків.

Рисунок 11.5 - Структура ЦА для пристрою множення чисел з фіксованою комою

Приклад. Помножити А_пр=11/11010 (-26); В_пр =00/11001 (25), С= -650.

РІШЕННЯ: Визначається знак добутку С: 1Å0 =1.

Приймемо:

1) суматор має 10 розрядів (без знака).

2) регістри мають по 5 розрядів (без знака).

Послідовність дій представимо таблицею 11.1

Для спрощення запису таблиць, приймемо наступні умовні позначки:

- оператор := привласнення значення (блоку ліворуч привласнюється значення, що є праворуч );

- позначення, наприклад, [См] - вміст суматора;

- оператор[]зсуву вмісту, наприклад, регістра А вправо наодин розряд;

- позначення В. П. - вхідне положення;

-позначення А_пр, В_пр- цифрова частина множенного, множника (прямий код).

Відповідь: С_пр= 11/1010001010.

Таблиця 11.1 - Приклад рішення

Якщо при множенні виникає одиниця переносу зі старшого розряду, то її зберігають шляхом зсуву суматора (å), тобто необхідно передбачати в ЦА стробування (фіксування) сигналу переповнення для виробу зсуву на один розряд вправо. Цей спосіб одержав найбільше поширення в практиці ЦА.

11.2.1 Множення чисел з рухомою комою

Числа у ФРК представляються мантисою і порядком, тому виконання операції множення складається із двох дій:

- перемножування мантис;

- додавання порядків.

Рисунок 11.6 - Структура ЦА для пристрою множення чисел у ФРК

Результат множення може вийти денормалізованим, тому потрібна перевірка на нормалізацію числа (критерій δ) та, при необхідності, його нормалізація з відповідною корекцією порядку Р результату. Пристрій множення чисел із рухомою комою представлено ЦА зі структурою рис. 11.6.

Таблиця 11.2 - Перемножування мантис А і В.

Приклад. А= -0,11001×2^-3; В=0,10011×2¹ (перемноження мантис здійсніть самостійно зг. п. 11.2. Суматор - 10 розрядів, Рг для А і В – по 5 розрядів). Додавання порядків робимо на ДСОК у ФРК.

 

[Р_А]_об =11/100

[Р_В ]_об=00/001

[P_С]_об=11/101 [С]_пр = 11/010; С_пр=-010₍₂₎

Тому що мантиса результату не задовольняє нормалізації (тобто δ=1, γ =0), то робимо зсув мантиси вліво на один розряд (див. табл.9.2) і проводимо корекцію порядку: m=11/1110110111.

₊[Р_С]_об = 11/101

[DР ]_об = 11/110

111/011

a→→1

[Р_С]’_об = 11/100; [Р_С]’_пр=11/011 (-3).

Відповідь: С= -0,1110110111×2^-3

 

11.2.2 Особливі випадки при множенні

При множенні можуть спостерігатися наступні особливі випадки:

- один зі співмножників = 0. Операція блокується з видачею результату С = 0;

- порядок результату дорівнює найбільшій негативній величині. Формується "0";

- множене найбільше і негативне число. Збільшується множене на 2^n-1 тобто, зсувається вліво.

Корекції роблять за допомогою аналізаторів, що вводять у ЦА.

ПРАВИЛО. Якщо в якості множника виступає число зі степінного ряду вагових значень бінарної системи, то множення проводиться зсувом числа вліво на число розрядів, що дорівнює ступені множника.

Приклад. Помножити А=+00011 (+3); В=+00100 (+4=2²). С=00011 ×00100= 00011×(2²)= 01100.