Объектов на основе их динамических моделей

 

1.1. Оперативное планирование и прогнозирование.

РАР-уравнение (2.2.11, Модуль 2) описывает временную последовательность или временной ряд. Наиболее просто анализ рядов такого вида проводить в предположении стационарности (квазистационарности) их коэффициентов, что характерно при оперативном планировании и прогнозировании. При этом можно считать, что a _{t , k} @ a _k, b_t1 @ b₁, b_t2 @ b₂.

Тогда уравнение (2.2.11) примет стационарный вид

S_t =+ b₁ C_1t + b₂ C_2t + H_t (1.1.1)

Как уже рассматривалось в параграфе 1.1 (Модуль 1) в общем виде линейная РАР- модель со стационарными коэффициентами описывается уравнением

S_t = ++ H_t (1.1.2)

Такая модель описывает, например, статическое воздействие на состояние ЭО управляющих финансовых факторов C_k,t , полученных из различных источников (k = 0, 1, 2, …, K), или динамическое воздействие, если C_k,t º C_k-t .

Если все структурные параметры (коэффициенты) динамического уравнения (1.1.2) известны, то при некоторых допущениях о характере поведения помехи H_t возможно определить значение S_t состояния ЭО в любой момент времени. Следовательно, возможно спланировать финансовые затраты, необходимые для достижения ЭО заданного (планового) значения S^*_n или «выхода» на плановую траекторию S^*_n+1, S^*_n+2, …, S^*_n+T к определенному моменту времени t = n (см. рис. 1.1.1).

Однако на практике часто бывает так, что известны не коэффициенты уравнения состояния ЭО, а лишь некоторые наблюдения (ряды) данных C₁, C₂, … , C_n и S₁, S₂, … , S_n для конкретного процесса. По этим эмпирическим данным необходимо спрогнозировать будущие значения S_n+1, S_n+2, … , S_m состояния ЭО.

 

 

 

 

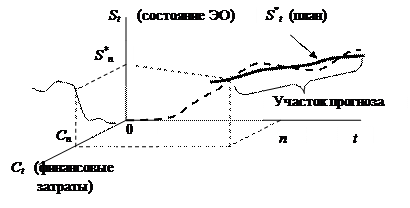РРис. 1.1.1

При этом возникают две проблемы:

- идентификация параметров уравнения (структурная идентификация ЭО) по этим эмпирическим данным;

- прогноз будущих значений S_n+1, S_n+2, … , S_m состояния ЭО на основе идентифицированных параметров.

Естественно, что основную роль в обоих случаях играет как характер помех, так и характер нестационарности параметров соответствующего динамического уравнения.

В экономике нестационарность параметров играет особенно важную роль в связи с изменчивостью условий производства, определяемых как его внутренней структурой (коэффициенты 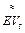и a_t), так и внешними рыночными условиями (коэффициенты P_t, tax_НДС, tax_t).

Обычно помеху описывают следующей моделью временного ряда

H_t = Seas_t + Sirc_t + E_t, (1.1.3)

где Seas_t – сезонный компонент, Circ_t – циклический компонент, E_t – стохастический компонент помехи. Часть Seas_t + Circ_t образует детерминированный компонент помехи.

Сезонный компонент отражает повторяемость процессов во времени и состоит из последовательности почти повторяющихся циклов. Типичным примером сезонного эффекта является объем продаж в преддверии праздников. Поэтому в некоторых временных рядах сезонный компонент может иметь плавающий или изменяющийся характер.

Циклический компонент занимает как бы промежуточное положение между детерминированной и стохастической составляющими временного ряда. Он описывает длительные периоды относительного подъема и спада и состоит из циклов, которые меняются по амплитуде и протяженности.

Следует отметить, что сезонный и циклический компоненты могут быть также решением РАР-уравнения (1.1.1). Тем самым, данные компоненты могут описывать не только помеху, но и закономерную динамику ЭО.

Стохастический компонент описывается обычно моделью Гаусса-Маркова (т.н. стационарного белого шума), в которой M E_t = 0, M(E_t E_t-k) = s ² d _k, где M означает операцию оценивания математического ожидания, а d ₀ = 1 и d _k = 0 для " k ¹ 0. Предполагают также, что все E_t распределены по нормальному (Гауссову) закону (см. главу 2, Модуль 1).

Обычно при оперативном планировании и прогнозировании рассматривают лишь стохастический компонент помехи. При этом из уравнения (1.1.1) получают различные частные случаи моделей временных рядов, поддающихся простейшему анализу.

Модель парной линейной регрессии.

S_t = a +bC_t + E_t , M(E_t) = 0, M(E_t E_{t - k})=s ² d _k (1.1.4)

для "t = 1,2,.., n.

Параметры модели оценивают по методу наименьших квадратов (МНК), выбирая a и b таким образом, чтобы минимизировать среднеквадратическую ошибку (СКО) аппроксимации

СКО == Þ min. (1.1.5)

Оценки коэффициентов регрессии находят, решая систему уравнений

¶СКО/¶a =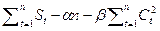= 0,

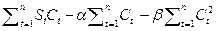¶СКО/¶b == 0.

 

Отсюда находим оценки коэффициентов модели через выборочные статистики (ковариацию, дисперсии)

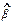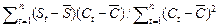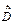== (S_t, C_t) /(C_t),

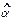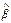
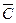=, (1.1.6)

где 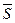= (1/n) , 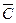= (1/n) 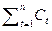– средние значения наблюдений.

Эмпирические оценки точности вычислений коэффициентов регрессии даются выражениями

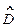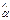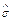() = ² [1+²/]/n, (1.1.7)

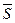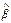() = ² /,

где 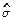² = (n-2)^-1 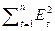= (n-2)^-1 .

Модель множественной линейной регрессии.

S_t= a + b₁C_t1 + b₂ C_t2 + … b_r C_tr + E_t, (1.1.8)

M(E_t) = 0, M(E_t E_{t - k}) = s ² d _k для " t = 1, 2, .. , n.

Используя векторные обозначения векторов-строк B⁺ = (a, b₁, b₂,… , b_r), E⁺ = (E₁, E₂, … , E_n) и матрицы C наблюдений

C = ,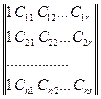

более кратко модель наблюдений (1.1.8) записывают в виде

S = C B + E . (1.1.9)

Параметры модели (вектор-столбец B) снова оценивают по методу наименьших квадратов, выбирая вектор-столбец B таким образом, чтобы минимизировать общую ошибку СКО = E⁺E

B = (C ⁺C ) ^-1 C ⁺ S, (1.1.10)

где (C ⁺C ) ^-1 – матрица, обратная (C ⁺C ), т.е. такая, которая при умножении на матрицу (C ⁺C ) дает единичную матрицу.

Модель стационарной авторегрессии первого порядка

АР(1).

S_t = a S_t-1 + E_t, M(E_t) = 0, M(E_t E_{t - k}) = s ² d _k , (1.1.11)

M S_t = m, cov(S_t, S_t-k) = M(S_t, S_t-k) для " t = 1, 2, .. , n.

Взяв математическое ожидание от обеих частей (1.1.11), получим m = a m. Следовательно, m = 0, если a ¹ 1. Взяв дисперсию от обеих частей (1.1.11) и учитывая, что D(S_t) = D(S_t-1) = cov(S_t, S_t), получим

D(S_t) = s ²/(1– a ²), (1.1.12)

cov(S_t, S_t-k) = a ^ks ²/(1– a ²), úaú < 1.

Отсюда следует, что автокорреляционная функция процесса cor(S_t, S_t-k) = cov(S_t, S_t-k)/ D(S_t) = a ^k убывает с ростом временного лага.

Минимизируя ошибку СКО = = , получим оценку коэффициента регрессии с помощью выборочного коэффициента корреляции

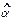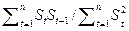= = . (1.1.13)

Модель стационарной авторегрессии второго порядка

АР(2).

S_t = a₁ S_t-1 +a₂ S_t-2 + E_t, M(E_t) = 0, M(E_t E_{t - k})=s ² d _k , (1.1.14)

M S_t = m, cov(S_t, S_t-k) = M(S_t, S_t-k) для " t = 1, 2, .. n.

Условие стационарности накладывает ограничения на коэффициенты модели

a₁ + a₂ < 1, a₁ – a₂ > – 1, a₂ > – 1. (1.1.15)

Используя (1.1.14), получим

cov(S_t, S_t-1) = a₁ cov(S_t, S_t) + a₂ cov(S_t, S_t-1),

cov(S_t, S_t-2) = a₁ cov(S_t, S_t-1) + a₂ cov(S_t, S_t).

Соответственно для автокорреляционных функций cor_k = cov(S_t, S_t-k)/cov(S_t, S_t) эти равенства дают так называемые уравнения Юла-Уолкера

cor₁ = a₁ + a₂ cor₁, cor₂ = a₁ cor₁ + a₂ , (1.1.16)

из которых определяются параметры АР(2)

a₁ = (cor₁ - cor₁ cor₂)/(1- cor²₁), a₂ = (cor₂ - cor²₁)/(1- cor²₁).

(1.1.17)

Для оценки параметров АР(2) по наблюдениям используют выборочные коэффициенты корреляции

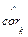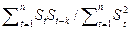= . (1.1.18)

Идентификация РАР модели состояний ЭО при

стационарных коэффициентах.

Используя метод наименьших квадратов, найдем коэффициенты РАР-модели типа (1.1.1) при всех известных значениях S_t и C_t (для упрощения управления C_1t и C_2t объединяются). Для этого будем минимизировать ошибку

СКО = Þ min. (1.1.19)

По аналогии с минимизацией (1.1.5) находим систему уравнений для отыскания коэффициентов a _k и b

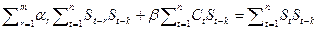, (1.1.20)

,

k = 1, 2, … m.

Полученная система m +1 уравнений решается численным способом.

Идентификация РАР модели состояний ЭО при

нестационарных коэффициентах.

Решим задачу идентификации нестационарных параметров упрощенного аналога уравнения (1.1.1), так называемого, РАР- уравнения 1-го порядка

S_t = a _t S_{t –1} + b _t C_t + H_t . (1.1.21)

При этом зададим линейную регрессию структурных параметров

a _t = a ⁰ + a ¹ t , b _t = b ⁰ + b ¹ t. (1.1.22)

Используя метод наименьших квадратов, получим систему уравнений, минимизирующую ошибку СКО

=

=,

=

= ,

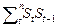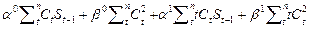(1.1.23)

=

= ,

=

= .

Естественно, что «наилучшее», например по критерию R² детерминации (см. стр. 16) или множественной корреляции, решение возможно получить при стохастическом характере помех, т.е., когда H_t = E_t.

Решив систему линейных уравнений (1.1.23) и воспользовавшись уравнением (2.2.11) при дополнительных предположениях (например, задав EV_t, P_t и tax_НДС), возможно найти, например, важные для задач аудита коэффициенты a_t , tax_t .

Коррелированность стохастической помехи.

При оперативном прогнозировании достаточно сложной является проблема коррелированности (зависимости) соседних значений стохастической помехи, когда ряд E_t стохастической переменной сам описывается, например, моделью АР(1): E_t = = r E_t-1 + x _t , M(x _t) = 0, M(x _t x _{t - k}) = s ² d _k для" t = 1, 2, .. , n. Для «парирования» данной ситуации в современных статистических пакетах используется алгоритмический метод Кокрана-Оркатта, включающий следующие этапы.

1. Делаются оценки 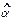, 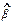коэффициентов регрессии (1.1.4).

2. Вычисляются остатки E_t = S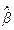_t – –C_t .

3. По формуле (1.1.13) делается оценка коэффициента r авторегрессионной зависимости E_t = r E_t-1 + x _t вычисленных остатков.

4. Делается замена наблюдений

= C_t – r C_t-1 и 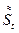= S_t – r S_t-1.

Рассматривается новое регрессионное уравнение

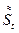= a (1– r) + b+ x _t, (1.1.24)

оценивание которого позволяет пересмотреть оценки a и b.

5. Повторно вычисляются остатки, и процесс возвращается к этапу 3.

6. Вычисления прекращаются, когда полученные оценки на последнем и предпоследнем циклах совпадают с заданной степенью точности.

1.2. Стратегическое планирование и прогнозирование.

Стратегическое планирование и прогнозирование связано с динамикой состояния ЭО в течение достаточно длительного периода времени – 10 ¸15 лет. Естественно, что на таком длительном периоде структурные параметры ЭО – коэффициенты динамического уравнения (1.1.2) – не могут оставаться постоянными – они подвержены либо некоторому тренду (Tr), либо сезонным и циклическим изменениям.

Считается, что тренд связан с долговременным воздействием (по сравнению с сезонными и циклическими колебаниями) на ЭО какого-либо плавно изменяющегося фактора, эффект от воздействия которого сказывается постепенно.

Обычно, исходя из знаний реальных условий, долгосрочный прогнозируемый период разбивают на периоды относительной стационарности структурных параметров и применяют к ним вышерассмотренные методы. Тем не менее, проблематичность стратегического прогнозирования легко пояснить с помощью рис. 1.2.1.

На рис. 1.2.1 приведен ряд А состояний некоторого ЭО для длительного периода (10 лет). Видно, что значения ряда подвержены сезонным и циклическим колебаниям. Ряд B получен из ряда А путем скользящего усреднения (сглаживания) последнего. В результате были устранены стохастические помехи. Кривые С и D, отвечающие различным периодам квазистационарности ЭО, построены с помощью оценивания нелинейных регрессионных зависимостей 3-го порядка на участке (0 ¸ 5) лет и 1-го порядка на участке (5 ¸ 7) лет. При этом сезонные колебания временно рассматривались как стохастическая помеха. На участке (7 ¸ 10) лет был сделан линейный постпрогноз (прогноз

«задним числом») – линия E.

Рис. 1.2.1

Заметим, что в стратегическом плане линейный прогноз верно отражает тенденцию увеличения значения прогнозируемого экономического показателя. В то же время, он проигрывает в плане долгосрочного прогнозирования, т.к. не отражает периоды подъема и спада (два подъема и три спада). Однако ситуацию легко исправить, наложив на линейный прогноз колебательный компонент с сезонным периодом и амплитудой, оцененными по кривой B. Для этого надо вычесть из кривой B полученный тренд C+D и рассчитать требуемые параметры. В то же время видно, что спрогнозировать тренд (постепенное увеличение) сезонной амплитуды на участке (5 ¸ 7) лет практически невозможно. Также невозможно по имеющимся данным сделать и настоящий прогноз за пределы 10 лет. Здесь может быть любая ситуация как подъема, так и спада технологического показателя. Заметим также, что использование линейной регрессии (вместо нелинейной) на участке (0 ¸ 5) лет не ухудшило бы полученный прогноз.

Из приведенного примера можно сделать важные выводы:

1. Линейный (полиномиальный) регрессионный анализ является самым простым и надежным методом отражения тенденций в стратегическом прогнозировании.

2. Линейный (полиномиальный) регрессионный анализ может быть легко скорректирован наложением сезонный компонент.

3. К прогнозу на длительный период нужно относиться скептически. Из практики считается, что прогноз возможен на период не более одной трети от периода имеющихся наблюдений.

4. Необходимо использовать некоторые формальные критерии качества регрессионных прогнозных моделей.

В общем случае для управления средствами в рамках стратегического планирования и прогнозирования необходимо использовать компьютерное имитационное моделирование, основанное на переборе возможных результатов, получаемых по моделям (1.1.1, 1.1.2) при различных структурных параметрах ЭОи помехах.

1.3. Критерии качества регрессионных моделей и

прогнозирования.

Качество регрессионной модели определяют ее адекватностью исследуемому процессу, характеризуемой выполнением определенных статистических свойств и точностью или степенью близости к фактическим данным.

Модель (1.1.1, 1.1.2) является адекватной, если ряд остатков S_t – 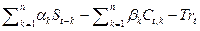обладает свойствами случайности, независимости последовательных отсчетов и нормальности распределений.

Используют следующие критерии.

1) P-критерий поворотных точек (случайности ряда остатков), где количество P поворотных точек должно удовлетворять строгому неравенству для случайного ряда остатков

P > целая часть{2(n–1)/3 – 2[(16n – 29)/90]^1/2}. (1.3.1)

Каждый отсчет ряда остатков сравнивается с двумя рядом стоящими, если он больше или меньше их, то этот отсчет считается поворотным.

2) DW-критерий независимости (Дарбина-Уотсона)

DW = 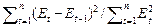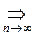2(1-).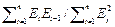

(1.3.2)

DW стремится к 2 при независимости соседних отсчетов ряда остатков.

3) RS -критерий нормальности случайных остатков, где

RS = (E_max – E_min)/ . (1.3.3)

RS характеризует попадание между табулированными границами с заданным уровнем вероятности (доверительный интервал) характеризует нормальность распределения ряда остатков.

Степень близости модели к фактическим данным характеризуется следующими критериями.

1) Детерминации (множественной корреляции) R², где

R² = 1 – 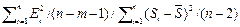. (1.3.4)

характеризует долю вариации зависимой переменной, объясняемой линейной регрессионной моделью (m – число независимых переменных, n – число наблюдений). Обычно 0,9 £ R² < 1.

2) TS – статистика (Стьюдента), где

TS = 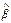/D^1/2(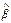). (1.3.5)

TS характеризует значимость оцениваемого коэффициента наклона в линейной регрессионной модели при заданном уровне (обычно 0,05), соответствующем доверительной вероятности 95 % и числе n – 2 степеней свободы.

3) F – статистика (Фишера), где

F = R² (n – m – 1) /(1 – R²) m. (1.3.6)

F используется для определения статистической значимости коэффициента детерминации R² путем проверки гипотезы о равенстве нулю всех коэффициентов (за исключением свободного члена) регрессии.

4) Доверительный интервал прогноза S = S_n+T по линейной регрессионной модели будет иметь следующие границы

S_Tmax = S_T + D S_T – верхняя граница, (1.3.7)

S_Tmin = S_T – D S_T – нижняя граница,

D S_T = TS [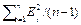]^1/2 *

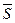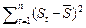*[1 +1/T + (S_n+T – )² /]^1/2.

Автоматизация прогнозирования ЭО по их РАР моделям поддерживается во многих современных статистических пакетах (например, Statistica в среде Windows).