Доверительные интервалы

 

Введем случайную величину

. (13.1)

Нетрудно проверить, что xÎN(0,1), вследствие чего

.

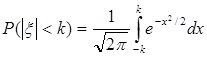Полагая 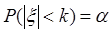, получим после элементарных преобразований, что с

вероятностью a выполняется неравенство

. (13.2)

Интервал называется доверительным интервалом, отвечающим доверительной вероятности a . Если, к примеру, k=2, доверительная вероятность a=0.955. Значению k=3 отвечает вероятность a = 0.997 (правило «трех сигм»). Но для использования указанных доверительных интервалов на практике нужно знать стандартное отклонение s. Если значение s неизвестно, для его оценки используется величина 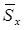. В этом случае можно ввести случайную величину

,

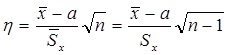которая имеет распределение Стьюдента с n-1 степенью свободы [3]. Не выписывая здесь соответствующей функции распределения, приведем несколько значений доверительной вероятности a(k, n), отвечающих доверительному интервалу

. (13.3)

При k=2 и n=3 имеем a=0.817; при k=2 и n=7 вероятность a=0.908 ;

a(3,3)=0.905; a(3,5)=0.96. С ростом n различие между распределением Стьюдента и Гауссовым распределением становится меньше, при n=20 этим различием в большинстве случаев можно пренебречь.

Регрессионные модели мы строим по данным наблюдениям (x_i,y_i), i = 1,2,....n. Пусть значения x = x^* не совпадают с x_i. Чему будет равна величина y = y^* и с какой погрешностью ее можно найти?

Попытаемся ответить на этот вопрос для случая парной линейной регрессии с нулевым свободным членом

y_i = bx_i + e_i ,

где e_iÎN(0,s), i = 1,2...n.

Параметр b оцениваем методом наименьших квадратов:

Se_i² = S(bx_i – y_i)² ® min,

S(bx_i – y_i)x_i = 0,

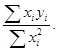= (13.4)

Из формулы (13.4) следует, что оценка является гауссовой случайной величиной с математическим ожиданием

E= = = 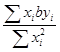b

(оценка несмещенная) и дисперсией

D= 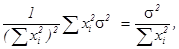(13.5)

Величина σ² , как правило, неизвестна и ее следует оценить. Для этого составим сумму квадратов ошибок

Se_i² = S(bx_i – y_i)² = S(bx_i –x_i +x_i - y_i)² =

= Sx_i² (b-)² + Σ(x_i –y_i)²+ 2Sx_i(b-)(x_i- y_i). (13.6)

Математическое ожидание ESe_i² = SЕe_i² = nσ².

Вычисление математического ожидания в правой части равенства (13.6) дает

Sx_i² D+ EΣ(x_i –y_i)²,

так как математическое ожидание последнего слагаемого равно нулю. Поэтому

nσ² = Sx_i² D+ EΣ(x_i –y_i)².

С учетом формулы (13.5) получим

(n-1)σ² = EΣ(x_i –y_i)² .

Теперь ясно, что величина

S ² = 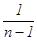Σ(x_i –y_i)² (13.7)

будет несмещенной оценкой для σ². Множитель (n-1) указывает на то, что, располагая только одним наблюдением (x_1, y₁), нельзя получить оценку S ², так как возникает неопределенность вида 0/0.

Для определения доверительного интервала оценки , отвечающего доверительной вероятности α, рассмотрим случайную величину

ξ = (b-),

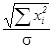имеющую нормальное распределение N(0,1). Заменив σ оценкой S , придем к случайной величине

η = (b-),

имеющей распределение Стьюдента с (n-1) степенями свободы. Для прогнозируемого значения y* регрессионная модель дает значение

y^* =x^* + e,

 

при этом Ey^* = bx^*, Dy^*=( x^*)²D+ De = σ² .

Заменим дисперсию σ² оценкой S² из (13.7):

(S_y^*)² = S ² .

Доверительный интервал для прогнозируемых величин y^* будет определяться распределением Стьюдента. Его границы вычисляются по формуле

y = y^* ± S_y^*t(n-1, 1-a/2),

где a - доверительная вероятность (например, a = 0,95), (n-1) – число степеней свободы. Статистические пакеты вычисляют эти границы и дают их графическое представление.

Совершенно аналогично рассматривается общий случай множественной линейной регрессии

y =Fq + e.

Можно показать, что

Dy^* = (x^*)^TQ x^* + s²,

где x_i = (x₁,x₂,...x_n)^*; Q = covq= s²(F^TF)^-1. Поэтому

Dy^* = s²[(x^*)^T (F^TF)^-1x^* +1].

Несмещенной оценкой для s ² является число

S ² = . (13.8)

Поэтому оценка среднеквадратичного отклонения y^* будет

S_y^* = S[(x^*)^T (F^TF)^-1x^* +1]^1/2,

а граница доверительного интервала

y = y^* ± S_y^*t(n-m, 1-a/2).