Модели кривых роста

Плавную кривую (гладкую функцию), аппроксимирующую временной ряд принято называть кривой роста.

 

Аналитические методы выделения (оценки) неслучайной составляющей временного ряда с помощью кривых роста реализуются в рамках моделей регрессии, в которых в роли зависимой переменной выступает переменная y_t, а в роли единственной объясняющей переменной - время t.

 

Наиболее часто в практической работе используются кривые роста, которые позволяют описывать процессы трех основных типов:

-без предела роста;

-с пределом роста без точки перегиба;

-с пределом роста и точкой перегиба.

 

Для описания процессов без предела роста служат функции:

 

- прямая (полином первой степени) - ,

 

- парабола (полином второй степени) - ,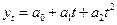

 

-экспонента - 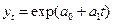и другие.

 

Процессы развития такого типа характерны в основном для абсолютных объемных показателей.

 

Например, объём продаж пива с1992 г. по 2003 г.[ Россия в цифрах. 2004. Госкомстат России. - М., 2004] (табл. 3.4.9) может быть описан полиномом второй степени (рис. 1.8).

 

Табл. 1.9. Продажа пива (млн. дкл.)

 

Годы
t
Пиво	273,3		411,7	408,2	451,1	524,6	634,6	707,8	762,5

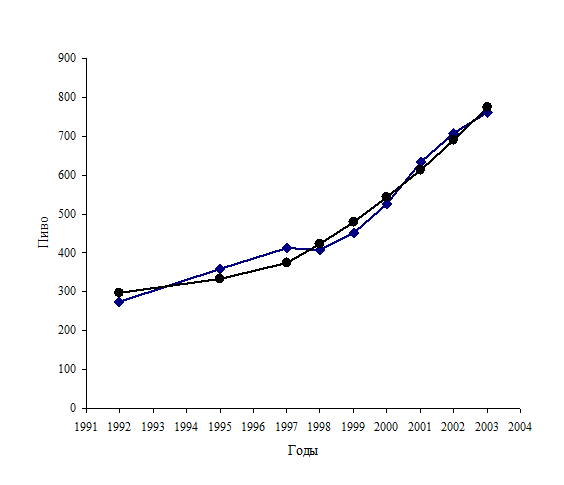
Рис. 1.8. Тенденция продаж пива (млн. дкл.) может быть описана полиномом второй степени .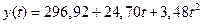

 

Для описания процессов с пределом роста служат функции:

- кривая Джонсона,

-модифицированная экспонента и др.

 

Процессы с пределом роста характерны для многих относительных показателей (душевое потребление продуктов питания, внесение удобрений на единицу площади, затраты на один рубль произведенной продукции и т.п.).

 

Для описания процессов третьего типа - с пределом роста и точкой перегиба используются кинетическая кривая (кривая Перла - Рида) и кривая Гомперца.

Такой тип развития характерен для спроса на некоторые новые товары.

 

Математические методы позволяют представить прогнозирующую модель в виде полинома любого порядка. Однако без необходимости использование полиномов высокого порядка представляется излишним.

 

Параметры моделей могут быть содержательно интерпретированы.

 

Так,

- параметр а₀ во всех моделях без предела роста задает начальные условия развития, а в моделях с пределом роста - асимптоту функций,

-параметр а₁ определяет скорость или интенсивность развития,

-параметр а₂ - изменение скорости или интенсивности развития.

 

Параметры большинства "кривых роста", как правило, оцениваются по методу наименьших квад­ратов, т.е. подбираются таким образом, чтобы график функции "кри­вой роста" располагался на минимальном удалении от точек исходных данных.

Согласно методу наименьших квадратов при оценке параметров модели всем наблюдениям присваиваются равные веса, т.е. их инфор­мационная ценность признается равной, а тенденция развития на всем участке наблюдений – неизменной.

 

Предпочтение, как правило, отдается простым моделям, допускающим содержательную интерпретацию.

 

К числу таких моделей относится линейная модель роста

, (1.14)

где – параметры модели, а t = 1, 2,…, n.

 

Математически критерий оценки параметров модели записывается в виде:

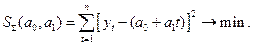(1.15)

 

Для нахождения минимума функции двух переменных 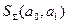следует взять частные производные по 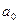и 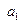, а затем приравнять их нулю.

 

 

В результате получим так называемую систему нормальных уравнений

 

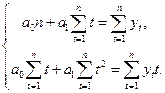(1.16)

 

 

Решая систему двух линейных уравнений с двумя неизвестными, получим

 

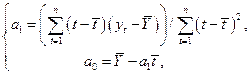(1.17)

 

где 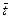и 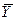– средние значения моментов наблюдения и уровней ряда, соответственно.