Теорема фон Неймана-Нэша
Для любой матричной игры 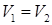 минимакс равен максимину, или − существуют
минимакс равен максимину, или − существуют 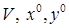 , удовлетворяющие условиям:
, удовлетворяющие условиям:


 .
.
1.3. Метод решения игры 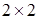
Рассмотрим игру 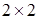 , т. е. когда у каждого из игроков имеются всего две стратегии (i = 1, 2; j = 1, 2).
, т. е. когда у каждого из игроков имеются всего две стратегии (i = 1, 2; j = 1, 2).
Поскольку при равенстве нижних и верхних цен игры в чистых стратегиях решение очевидно (оно определяется седловой точкой матрицы), интерес представляет ситуация их неравенства. Но из теоремы Неймана-Нэша следует, что существует пара смешанных стратегий 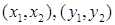 , обеспечивающая равенство верхней и нижней цены игры (минимакса и максимина). Раз это не реализуется чистыми стратегиями, значит, цена игры V достигается при смешивании каждым игроком обеих своих стратегий (обе стратегии «активны») и при каждой чистой стратегии противника (иначе никакое смешивание не может улучшить результат), поэтому если
, обеспечивающая равенство верхней и нижней цены игры (минимакса и максимина). Раз это не реализуется чистыми стратегиями, значит, цена игры V достигается при смешивании каждым игроком обеих своих стратегий (обе стратегии «активны») и при каждой чистой стратегии противника (иначе никакое смешивание не может улучшить результат), поэтому если
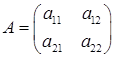 , то
, то 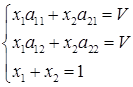 (1.3.1)
(1.3.1)
Имеем три уравнения с тремя неизвестными. Вычитая из первого уравнения второе, получаем отношение
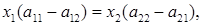
 (1.3.2)
(1.3.2)
Знак абсолютной величины поставлен потому, что это отношение всегда положительно, так как при разных знаках у 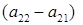 и
и 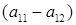 одна из стратегий второго игрока явно хуже другой и не может им применяться.
одна из стратегий второго игрока явно хуже другой и не может им применяться.
Решение отношения (1.3.2) сводится к делению единичного отрезка на части, находящиеся в отношении 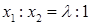
 ,
,
после чего найти 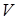 не представляет труда.
не представляет труда.