Методика отыскания оптимального решения
Рассмотрим задачу оптимизации плана производства (задача 1 тема 2):

При x1 ≥0 и x2≥0
Суммарная прибыль
F =2x1+3x2 → max
С помощью дополнительных переменных перейдем от стандартного вида к каноническому:
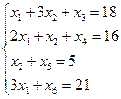
Для нахождения базисного решения необходимо выделить 2 группы переменных:
- основные, т.е. такие m-переменных, каждая из которых входит только в одно из m-уравнений системы ограничений, при этом нет таких уравнений, в которые бы не входила ни одна из этих переменных. Коэффициенты основных переменных должны быть равны +1;
- не основные – все остальные переменные. Для реализации задачи симплекс-методом используют следующий алгоритм:
Первый шаг:
Основные переменные:х3, х4, х5, х6.
Неосновные переменные: х1, х2.
Bыразим основные переменные через неосновные:


Подчеркнутое уравнение является разрешающим уравнением для второго шага.
Неосновные элементы считаем равными 0: х1=0, х2=0, тогда базисное решение A1(0;0;18;16;5;21). Это одно из возможных решений, но нельзя считать, что оно является оптимальным. Оно соответствует началу координат графика О (0;0)
Далее выражают функцию оптимизации через неосновные переменные:
F =2x1+3x2 → max
Для принятия решения важно проанализировать функцию F. Если есть хотя бы при одной переменной коэффициент К>0 в задаче на max, то рассматривают поведение функции F при увеличении значения соответствующей переменной.
Рассмотрим переменную х2, , т.к. К=3>0, то при увеличении значения х2 значение функции F возрастает, значит, решение А1 не является оптимальным.
Можно рассматривать и переменную х1, т.к. коэффициент при x1 =2>0. Однако, при выборе анализируемой переменной оценивают коэффициент при ней. Как правило, чем выше коэффициент, тем менее трудоемкой является задача в своем решении.
Следовательно, рассматриваем переменную х2, и она переходит из неосновных в основные. Геометрический смысл преобразований сводится к переходу к следующей вершине многогранника возможный решений, где значение функции становится лучшее.
Основная переменная должна иметь коэффициент К=1.
Для приведения системы ограничений в решаемый вид на следующем этапе для новой основной переменной, выражая ее из всех уравнений системы ограничений при условии, что все остальные переменные = 0.

Выбирают самый минимальный разрешающий коэффициент (х2 = 5), который в нашем примере соответствует 3-ему уравнению. Тогда х5 переходит в неосновные переменные. Уравнение, из которого была выражена переменная, называется разрешающим (х5 = 5 - х2).
Второй шаг:
Основные переменные:х2, х3, х4, х6.
Неосновные переменные: х1, х5.
Выразим новые основные переменные через неосновные, начиная с разрешающего уравнения:
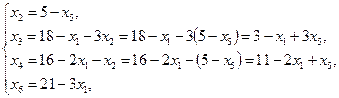
Подставим вместо х2 его выражение:
|

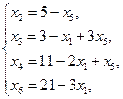
Неосновные переменные приравниваются к 0: х1 = 0 и х5 = 0, тогда второе базисное решение А2(0;5;3;11;0;21). Геометрически мы перешли к вершине А (0;5) в многоугольнике решений (Тема 2, раздел 2). Выразим функцию F через неосновные переменные:
F2=2x1+3x2=2x1+3(5-x5)=2x1+15-3x5
При увеличении значения переменной х1 значение функции F2 будет увеличиваться, значит, решение А2 не является оптимальным.
Найдем разрешающие коэффициенты для переменной х1:
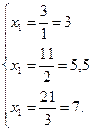
Выбираем самый минимальный разрешающий коэффициент x1=3. Уравнение, из которого была выражена переменная (x3 = 3 - x1+ 3x5) является разрешающим. Переменная x3 переходит в неосновные переменные, а х1 - в основные.
Третий шаг
Основные переменные: х1, х2, х4, х6.
Неосновные переменные:х3, х5.

|
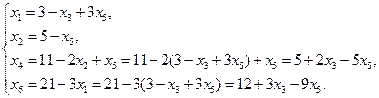
Базисное решение А3 (3;5;0;5;0;12) соответствует вершина Е(3;5)
F3=2x1+3x2=2(3-x3+3x5)+3(5-x5)=21-2x3+3x5
При х3 =0, х5 = 0 значение F3 = 21, что больше F2 = 15 на 6.
Увеличивая значение х5 значение функции будет также увеличиваться. Переведем х5 в основные переменные.
Найдем разрешающие коэффициенты х5:
|
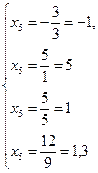
Разрешающим уравнением является х4 = 5 + 2х3 - 5х5, из которого 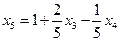 .
.
Переменная х4 переходит в неосновные.
Четвертый шаг
Основные переменные:х1, х2, х5, х6.
Неосновные переменные:х3, х4.
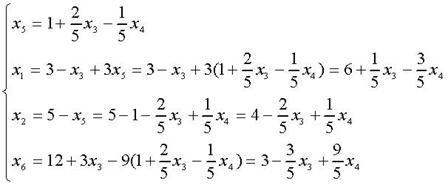
Базисное решение А4 (6;4;0;0;1;3) соответствует вершине В (6;4)
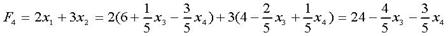
Это выражение функции не содержит переменных с положительными коэффициентами. При х3=0, х4=0 значение F4 является максимальным. Зная экономический смысл переменных, получаем, что максимальное значение прибыли – 24 руб. при реализации продукции А – 6 ед., продукции В – 4 ед. Дополнительные переменные х3, х4, х5, х6 показывают разницу между запасами ресурсов каждого вида и их потреблением на производство продукции А и В, т.е. остатки ресурса S1=0, S2=0, S3=1, S4=3 ед.
Таким образом, задачу на максимум решают до тех пор, пока в выражении линейной функции через неосновные переменные останутся отрицательные коэффициенты при неосновных переменных.
При отыскании минимума функции возможны 2 варианта:
1. отыскивать максимум функции, учитывая, что Zmin= - Fmax;
2. на каждом шаге рассматривать неосновные переменные, при которых стоят отрицательные коэффициенты, т.к. увеличивая значения этих переменных, значение функции будет уменьшаться, т.е. постепенно стремиться к min.
Критерием оптимальности при отыскании min функции является следующее правило:
| Если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение является оптимальным. |
При решении задачи симплекс-методом не всегда возможно сразу выделить допустимое базисное решение.
Например:
F=x1+2x2 → max

x1 ≥ 0 и x2 ≥ 0.
Решение:
1. Вводим дополнительные переменные:
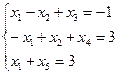
2. Выделим основные переменные х3, х4, х5 неосновные переменныех1, х2
3. Выразим основные переменные через неосновные:
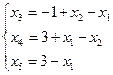
Базисное решение А1 (0;0;-1;3;3) является недопустимым, т.к. х3< 0.
В таком случае в системе уравнений выбирают то уравнение, которое содержит отрицательный свободный член (х3= -1 - х1 + х2).
Необходимо увеличить значение х3. Это возможно за счет увеличения переменных, входящих в уравнение с положительным коэффициентом (+х2).
При х2 =1 и х3 =0. Тогда х3 станет неосновной, х2 - основной переменными.
Найдем разрешающий коэффициент для переменной х2
x2=min{1;3}=1
Тогда уравнение x3= -1 + x2 – x1 является разрешающим
На втором шаге основными переменными станут х2, х4, х5, а неосновными х1, х3.
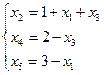
Базисное решение А1(0; 1; 0; 2; 3) является допустимым
F=x1+2x2=x1+2(1+x1+x3)=2+3x1+2x3, и т.д.
Бывают задачи, когда допустимое базисное решение возникает со 2, 3 и т.д. шагов.
Если базисное решение является недопустимым и для его улучшения есть возможность выбора переменной, то рекомендуют выбрать такую неосновную переменную, которая определит в качестве разрешающего то уравнение системы, где содержится отрицательный свободный член, и перевести в основные ту неосновную переменную, которая в это уравнение входит с положительным коэффициентом.
Если базисное решение недопустимое, а в уравнении, содержащем отрицательный свободный член, отсутствует неосновная переменная с положительным коэффициентом, то допустимое базисное решение получить невозможно, т.к. условия задачи являются противоречивыми.
При решении экономических задач симплекс-методом могут возникнуть ситуации, когда оптимальное решение будет неединственным (альтернативным), или конечный оптимум может отсутствовать. В первом случае, выбор оптимального варианта зависит от эксперта, принимающего решения, во - втором случае необходимо задать дополнительные условия – ограничений для принятия решения.