Для составления двойственной задачи используют следующий алгоритм.
1. Приводят все неравенства системы ограничений в исходной задаче к виду «≤», если F(x) → max и к виду «≥», если F(x) → min. Для этого неравенства, где не выполняется это условие, умножают на «-1».
2. Составляют матрицу системы А, в которую включают коэффициенты переменных, свободные члены и строку коэффициентов при переменных в линейной функции.
3. Составляют транспонированную матрицу A’
4. Формулируют двойственную задачу на основе матрицы A’, сохраняя экономический смысл обозначений.
Например. Составим двойственную задачу:
F= – x1+2x2 → max
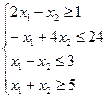
x1≥0, x2≥0
Приведем неравенства к виду «≤»:

Составим расширенную матрицу системы :
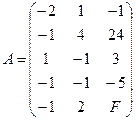
Cоставим транспонированную матрицу A’:

Двойственная задача примет вид:
Z = – y1+24y2+3y3 –5y4 → min
при ограничениях

y1 ≥ 0, y2 ≥ 0, y3 ≥ 0, y4 ≥ 0
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем:
ТЕОРЕМЫ
1. Для любых допустимых решений x и y справедливо неравенство: F(x) ≤ Z(y) или
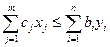 2. Если для допустимых решений x’ и y’ выполняется условие F(x’) = Z(y’), то x’- оптимальное решение исходной задачи и y’- оптимальное решение двойственной задачи.
3. Если одна из двойственных задач имеет оптимальное решение, то его имеет и другая задача
4. Если линейная функция одной из задач не ограничена (например: Fmax=∞ ), то условия другой задачи являются противоречивыми.
2. Если для допустимых решений x’ и y’ выполняется условие F(x’) = Z(y’), то x’- оптимальное решение исходной задачи и y’- оптимальное решение двойственной задачи.
3. Если одна из двойственных задач имеет оптимальное решение, то его имеет и другая задача
4. Если линейная функция одной из задач не ограничена (например: Fmax=∞ ), то условия другой задачи являются противоречивыми.
|
Экономический смысл указанных теорем: применительно к нашему примеру план производства x’(x1’x2’…xn’) и цены y’(y1’y2’…ym’) на ресурсы являются оптимальными только тогда, когда выручка (прибыль) от реализации продукции по ценам сi (i=1,2,...n) равна затратам на ресурсы по ценам yi (i=1,2,...m). Для всех других планов производства X(x1, x2… xn) и цен Y(y1, y2…ym) прибыль от реализации продукции будет меньше или равна затратам на ресурсы, или предприятию экономически все равно производить продукцию по оптимальному плану x’ и получать максимальную прибыль F’, либо продать ресурсы по оптимальным ценам y’.
Для решения двойственных задач используют симплекс-метод. Для этого системы ограничений приводят к каноническому виду, вводя дополнительные переменные.
Связь между переменными следующая:
| Переменные исходной задачи | |||||||||||
| Первоначальные | Дополнительные | ||||||||||
| x1 | x2 | … | xj | … | xn | xn+1 | x n+2 | … | xn+i | … | xn+m |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ||||
| ym+1 | ym+2 | … | ym+j | … | ym+n | y1 | y2 | … | yj | … | ym |
| Дополнительные | Первоначальные | ||||||||||
| Переменные двойственной задачи |
При этом положительным (>0) компонентам оптимального решения одной из задач соответствуют нулевые компоненты оптимального решения другой задачи.
Например: если xj’>0, то y’m+j=0 и наоборот, если y’j>0, то x’n+i=0.
Для решения двойственных задач можно использовать следующее правило: компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.
Например: задача оптимизации плана производства.
Решим двойственную задачу симплекс-методом
| Исходная задача | Двойственная задача |
Оптимальное решение
X’=(6;4;0;0;1;3)
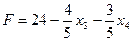 при Fmax=24 при Fmax=24
| Оптимальное решение

|
| Fmax=Zmin=24 |
Компоненты оптимального решения двойственной задачи:
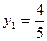
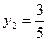 у3=0 у4=0 у5=0 у6=0
у3=0 у4=0 у5=0 у6=0
 .
.
Они равны значениям по абсолютной величине коэффициентов соответствующих переменных линейной функции:

И, наоборот, если симплекс-методом решили двойственную задачу и получили оптимальное решение  , то Z=24+y3+3y4+6y5+4y6, тогда оптимальное решение исходной задачи будет :
, то Z=24+y3+3y4+6y5+4y6, тогда оптимальное решение исходной задачи будет :
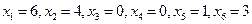
Х=(6;4;0;0;1;3) – является оптимальным решением исходной задачи
| Первоначальные переменные | Дополнительные переменные | ||||
| 4/5 | 3/5 | ||||
| x1 | x2 | x3 | x4 | x5 | x6 |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ |
| у5 | у6 | у1 | у2 | у3 | у4 |
Метод двойственной задачи обычно применяют, когда первое базисное решение исходной задачи является недопустимым, или когда число ограничений m в исходной задаче больше числа переменных x.
Экономический смысл двойственной задачи состоит не только в оценке оптимального объема производства, оптимальной цены реализации сырья, но и в оценке влияния запасов на величину прибыли предприятия, т.е. оценки (цены) ресурсов показывают, на сколько денежных единиц изменится максимальная прибыль (выручка) от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.
Из рассмотренного примера оптимальные цены ресурсов:
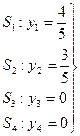
Таким образом, при увеличении запаса S1 на 1 единицу прибыли увеличится на 4/5 рубля. При увеличении запаса ресурса S2 - прибыль увеличится на 3/5 рубля. Увеличение S3, S4 запаса на прибыль влияния не окажет.
Двойственная задача дает возможность анализа решений при изменении или дополнения условий.
Например: предприятие решило производить и продукцию С, затраты сырья на ее производство следующие:
S1:a13 = 3 ед.
S2:a23 = 2 ед.
S3:a33 = 4 ед.
S4:a43 = 1 ед.
Цена единицы продукции С равна 3 рубля. Важно определить, даст ли прибыль включение в план производства продукции С и какой должна быть цена, чтобы производство продукции С было рентабельным?
Задачу можно решить заново, включая дополнительные условия. Однако, имея оценку ресурсов, можно сопоставить дополнительные затраты на ресурсы в связи с производством продукции С и цену реализации продукции.
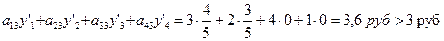
Значит, выпуск продукции С при цене за единицу продукции 3 рубля, является нерентабельным и включать ее в план производства нецелесообразно.
Для того, чтобы производство продукции С стало экономически выгодным, цена ее реализации должна быть более 3,6 руб.
По двойственной задаче можно определить и нормы заменяемости ресурсов при сохранении max прибыли. Для этого находят отношение оценок ресурсов:
 ,
,
т.е.
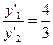 или
или 
Это означает, что каждые дополнительные 3 единицы ресурса 1 вида эквивалентны 4 единицам ресурса 2 вида, при этом прибыль остается неизменной (максимальной).