Экономическая сущность транспортной задачи, ее постановка и область применения в принятии оптимального экономического решения
Транспортная задача в основном связана с распределением товаров между поставщиками и потребителями таким образом, чтобы общая стоимость этого распределения была минимальной.
Для решения транспортной задачи необходим ряд обязательных условий:
- должны быть известны стоимость единицы продукции и стоимость ее из каждого пункта производства, в каждый пункт назначения;
- должен быть известен запас продукции в каждом пункте производства;
- должны быть известны потребности в каждом пункте потребления;
- общее предложение должно быть равно общему спросу.
Алгоритм решения транспортной задачи сводится к следующему:
- во-первых,исходные данные отражают в виде наглядной таблицы, где допустимым называют такое распределение ресурсов, которое позволяет удовлетворить весь спрос в пунктах потребления и вывести весь запас из пункта производителя;
- во-вторых,проверяют допустимое распределение ресурсов на оптимальность;
- в третьих,если полученное распределение не является оптимальным, то ресурсы перераспределяются с учетом снижения стоимости их транспортировки;
- в четвертых, каждое перераспределение ресурсов проверяется на оптимальность до тех пор, пока не будет получено оптимальное решение.
Пример: Имеются три поставщика и четыре потребителя. Мощность поставщиков и спрос потребителей, затраты на перевозку единицы груза сведены в таблицу поставок.
| Поставщики | Мощность поставщиков | Потребители и их спрос | |||
| А (1) | В (2) | С (3) | D (4) | ||
| А(1) | 1 у.е. x11 | 2 у.е. x12 | 5 у.е. x13 | 3 у.е. х14 | |
| В(2) | 1 у.е. х21 | 6 у.е. х22 | 5 у.е. Х23 | 2 у.е. х24 | |
| C(3) | 6 у.е. х31 | 3 у.е. х32 | 7 у.е. х33 | 4 у.е. х34 |
В левом верхнем углу обозначена стоимость перевозки единицы груза от i-того поставщика к j-ному потребителю. Необходимо найти оптимальный объем перевозок для каждой пары «поставщик-потребитель» так, чтобы:
1. Мощности всех поставщиков были реализованы;
2. Спрос всех потребителей был бы удовлетворен;
3. Суммарные затраты на перевозку были бы минимальными.
Пусть хij – объем перевозимого груза от i-того поставщика к j-тому потребителю.
Система ограничений по мощности поставщиков:
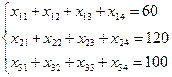
Условие, когда спрос потребителей должен быть удовлетворен:
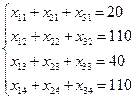
Суммарные затраты на перевозку:
F=x11+2x12+5x13+3x14+x21+6x22+5x23+2x24+6x31+3x32+7x33+4x34→min
Правила построения модели транспортной задачи:
1. Система ограничений всегда представляется в виде уравнений;
2. Коэффициенты при переменных в системе ограничений равны 1 или 0;
3. Каждая переменная входит в систему ограничений 2 раза: один раз – по строке; второй раз – по столбцу.
В общем виде модель транспортной задачи может быть представлена:
где Mi - мощности поставщиков, m – число поставщиков;
,
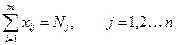где Nj – мощность (спрос) потребителей, n – число потребителей.
где Сij - коэффициенты затрат на перевозку.
Если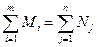 
, то задача называется закрытой.
В другом случае – открытая задача.
Транспортная задача может быть решена симплекс-методом. Однако, существует упрощенный метод – распределительный метод, в котором решение осуществляется по шагам, где каждый раз переменные разбивают на основные (базисные) и неосновные (свободные). Число основных переменных в закрытой задаче должно быть равно m+n-1.
Для нахождения первоначального базисного распределения поставок используют в основном 2 метода:
1. метод “северо-западного” угла;
2. метод наименьших затрат.
Рассмотрим метод «северо-западного» угла
При этом методе распределения поставок начинается каждый раз с левого верхнего угла на первом шаге – х11. Рассмотрим максимально возможное удовлетворение спроса первого потребителя.
После распределения первому потребителю 20 ед. продукции от первого поставщика спрос первого потребителя будет полностью удовлетворен, тогда последующее рассмотрение поставок от 2, 3 поставщиков для первого потребителя не имеет смысла.
Рассмотрим следующий «северо-западный» угол – х12. Спрос составляет 110 ед., у первого поставщика осталось всего 40 ед. продукции (60-20=40). После этого мощность первого поставщика полностью реализована и первая строка выпадает из дальнейшего распределения.
x22 –70 (110-40). Тогда для реализации мощности 2 поставщика в 120 ед. объем поставок для x23 составит 40 ед., для х24 – 10 ед.
Число заполненных клеток в исходном распределении должно удовлетворять условию m+n-1=3+4-1=6 и равно числу основных переменных. Таким образом, на каждом шаге из рассмотрения должна выпадать либо строка, либо столбец.
Существенным недостатком метода «северо-западного» угла является слабое внимание к значениям коэффициентов затрат на перевозку грузов.
Этот недостаток устраняется в методе наименьших затрат:
1. Находим в таблице поставок клетки с наименьшим коэффициентом затрат. Это клетки x11, x21.
2. Сравним максимально возможные поставки для этих клеток: x11-20, x21-20. Если значения совпадают, то выбираем любую из них, например x12. Тогда спрос первого потребителя будет удовлетворен.
Выбираем из оставшихся позиций клетки с наименьшими затратами x12 , x24, где c12=c24=2. Сравниваем максимально возможные поставки для этих клеток x12 = 60, x24= 100 и выбираем клетку с max поставкой (x24) и так далее.
| - | - | - | ||
| - | - | |||
| - |
Таким образом, полученное распределение можно называть базисным, если на каждом шаге (кроме последнего) из рассмотрения выпадают либо одна строка, либо один столбец.
Полученные базисные распределения различными методами могут не совпадать. Это свидетельствует о разном количестве шагов к достижению оптимального решения.
При решении задачи могут возникать особые случаи, когда число заполненных клеток окажется меньше, чем число базисных переменных, т.е. условие, чтобы число заполненных клеток должно быть равно (m+n-1) не выполняется.
Тогда используют искусственный прием: допускают фиктивное распределение поставок, которое равно нулю, в ту клетку, при рассмотрении которой выпадают либо строка, либо столбец.
Например:
| - | |||
| - | |||
| - | - |
Транспортная задача – это задача на минимум, поэтому оптимальное решение достигается тогда, когда все коэффициенты при неосновных переменных в линейной функции станут неотрицательными (≥0).
Оценка свободной клетки не изменится, если к коэффициентам затрат некоторой строки или столбца таблицы поставок прибавить некоторое число – потенциал данной строки или столбца.
Тогда находят такие числа (потенциалы), при сложении с которыми коэффициенты затрат в заполненных клетках стали бы равны нулю. Изменение коэффициентов затрат возможно с любой строки или столбца, начальный потенциал может быть любым числом.
Начнем рассмотрение переменных с 1-го столбца. Пусть его потенциал равен 0. Тогда c21 не изменится. Для достижения c21 = 0 потенциал второй строки должен быть равен – 1. Тогда для достижения c24 = 0 потенциал 4-го столбца должен быть равен –1 (2+(-1)+(-1)=0). Потенциал 3-ей строки равен –3 (4+(-1)+(-3)=0) и т.д.
| Потенциал | |||||
| - | - | - | -2 (7) | ||
| - | - | -1 (2) | |||
| - | -3 (4) | ||||
| Потенциал | 0 (1) | 0 (6) | -4 (5) | -1(3) | - |
Составим матрицу оценок из измененных коэффициентов затрат. Для этого к существующим коэффициентам затрат добавляют соответствующие потенциалы соответствующих столбца и строки.
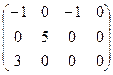
Базовое распределение поставок не является оптимальным, т.к. среди оценок свободных клеток существуют коэффициенты со знаком «-», а задача на минимум решается до тех пор, пока при свободных переменных существуют отрицательные коэффициенты.
Найдем F0 из первоначального распределения поставок методом наименьших затрат:
Для решения задачи, как и в симплекс-методе, рассматриваем неосновную переменную с отрицательным знаком, как правило, имеющую больший коэффициент. С отрицательными знаками имеем 2 переменные – х11, х13, но c11=1, c13=5, значит, для последующего перераспределения выберем переменную х13 и переведем ее из неосновных в основные. Для этого построим для переменной х13 означенный цикл пересчета.
Означенный цикл перерасчета представляет собой ломаную линию, соединяющую клетки с изменяемыми поставками, при этом ломаная должна быть связной, т.е. из любой ее вершины можно было бы попасть в любую другую вершину по звеньям ломаной не отрывая руки; в каждой вершине должны встречаться одно звено по столбцу, другое – по строке.
Таким образом для нахождения оценки сводной клетки следует построить означенный цикл пересчета, в вершине которого расставить чередующие знаки,"+" и "-", начиная с "+" в свободной клетке.
Для каждой свободной клетки базисного распределения существует единственный означенный цикл пересчета.
Объем поставки, передаваемой по циклу, для снижения трудоемкости решения задачи определяется как минимальное значение из поставок означенного цикла в клетках со знаком « - »:
Тогда перераспределение поставок будет иметь следующий вид:
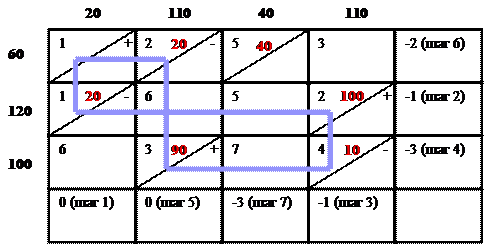
Полученное перераспределение является базисным, так как m+n-1=3+4-1=6 и число заполненных клеток тоже равно 6.
Далее проверяем базисное решение на оптимальность. Для этого подберем потенциалы так, чтобы коэффициенты затрат заполненных клеток стали равны нулю. Тогда матрица оценок примет вид:
.
Среди свободных клеток есть х11 с отрицательным коэффициентом, значит базисное решение не оптимально. Строим означенный цикл для переменной х11. Объем передаваемой поставки 
. Тогда новое распределение примет вид:
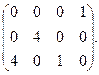
Среди оценок свободных клеток нет отрицательных значений, значит базисное распределение является оптимальным.
Тогда суммарные затраты на перевозку составят:
.
Таким образом, оптимальное распределение поставок позволило получить экономию денежных средств в 50 у.е.:
При решении транспортной задачи возможны особые случаи:
1. постановка передаваемая по циклу, может быть равна 0;
2. если при перераспределении поставок сразу в нескольких клетках поставка становится равной 0, то свободной из них считают только одну клетку (любую из них), остальные считаются заполненными, чтобы выполнялось условие (m+n-1);
3. открытую задачу необходимо свести к закрытому виду. Для этого вводят формально дополнительную либо строку, либо столбец, определяют размер ограничения, а коэффициенты затрат, как правило, равны 0. Далее задачу решают изученным способом.
Таким образом, алгоритм решения транспортной задачи сводится к следующему:
1. Для базисного решения (удовлетворяющего условию (m+n-1)) подбирают потенциалы строк и столбцов так, при сложении с которыми коэффициенты затрат заполненных клеток стали бы равны 0. Составляют матрицу оценок.
2. Если оценки всех свободных клеток неотрицательны т.е.>0, то найденное распределение оптимальное. Если имеются отрицательные значения, то выбирают одну переменную для формирования поставки (чаще всего выбирают клетку с наименьшей оценкой или наибольшим коэффициентом затрат).
3. Для выбранной клетки строят означенный цикл пересчета. Поставка U1, передаваемая по циклу, определяется как минимум из поставок в клетках со знаком « - » и найденный объем поставок передвигается по циклу.
При этом поставка в клетках со знаком «+» увеличивается на U, а в клетках со знаком « - » уменьшается на U. Клетка с поставкой, равной 0, будет считаться свободной, остальные клетки – заполненными. И новое базисное решение вновь анализируется в последовательности п.1 – п.3 настоящего алгоритма.