Методика решения экономических задач с использованием теории игр

В качестве основного документа в теории игр предполагается, что каждый игрок стремиться обеспечить себе максимально возможный выигрыш при любых действиях партнера. Пусть игрок 1 считает, что какую бы стратегию он ни выбрал, игрок 2 выберет стратегию, максимализирующую его выигрыш и минимизирующую выигрыш игрока 1.

Оптимальная стратегия игрока 1, которая обеспечивает ему наибольший выигрыш вне зависимости от стратегии противника, будем состоять в выборе стратегии с самым высоким выигрышем, т.е. игрок 1 выберет i-тую стратегию, которая является решением задачи:

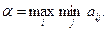
Значение α называют нижней ценой игры, или максимальным выигрышем (максимином), означающим гарантированный выигрыш игрока 1 при любой стратегии игрока 2.

Игрок 2 также стремится получить наибольшую величину выигрыша вне зависимости стратегии игрока 1, что равнозначно стремлению к получению наименьшей величины проигрыша. Таким образом, игрок 2 выберет j-стратегию, которая является решением задачи:

Значение 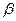называют верхней ценой игры, или минимаксом, что означает гарантированный проигрыш игрока 2.

Если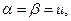то их значение 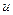называют чистой ценой игры. Минимаксные стратегии, соответствующие цене игры, являются оптимальными, а их совокупность - оптимальным решением игры, т.е. игрок 1 получает максимально гарантированный выигрыш, а игрок 2 – минимально гарантированный проигрыш. Если один игрок придерживается своей оптимальной стратегии, то другому игроку нецелесообразно отклоняться от своей оптимальной стратегии.

Пара стратегий игроков 1 и 2 дает оптимальное решение игры, только тогда, когда соответствующий ей элемент a_ij является одновременно в своем столбце и наименьшим в своей строке. Такую ситуацию еще называют седловой точкой.

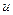Если, то игра не имеет седловой точки, тогда оптимальное решение возможно получить при случайном чередовании возможных стратегий. Тогда, выигрыш , соответствующий оптимальному решению, удовлетворяет неравенству: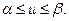

Решение экономических задач, описанных игровыми моделями, могут быть решены методом линейного программирования.

Например: Предприятие может выпускать три вида продукции (А₁, А₂ , А₃) получая при этом прибыль, зависящую от спроса, который может быть в четырех состояниях(В₁, В₂ , В₃, В₄). Каждому j -тому состоянию спроса соответствует размер прибыли от реализации i – того вида продукции. Определить оптимальные пропорции в выпуске продукции, которые гарантировали бы получение средней прибыли при любом состоянии спроса, считая его неопределенным.

Решение:

Платежная матрица

Спрос / продукция	B1	B2	B3	B4
А1
А2
А3

В данной игре в качестве игроков выступает предприятие против спроса. Проведем анализ платежной матрицы и отбросим стратегии, дублирующие друг друга или заведомо невыгодные. Стратегии характеризуют столбцы матрицы. Вторая стратегия является явно невыгодной для игрока В, т.к. его цель уменьшить выигрыш игрока А. Поэтому второй столбец можно отбросить.

Получим платежную матрицу:

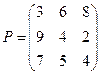Определим нижнюю и верхнюю границы цены:

- по строкам:

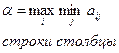
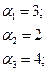
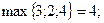
- по столбцам:

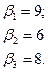
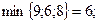
, значит седловая точка отсутствует и оптимальное решение следует искать в смешанных стратегиях игроков:

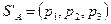и ,

где Рi , q_j- вероятности применения чистых стратегий.

Для оптимальной стратегии 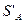все средние выигрыши должны быть не меньше цены игры при любой стратегии игрока В и выигрыш, равный 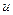при оптимальной стратегии В.

Значит получим систему неравенств:

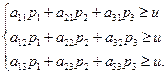
Разделим каждое неравенство на и введем новые переменные:

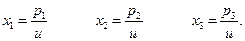
Тогда система ограничений будет иметь вид:

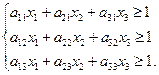
Сумма вероятностей всех событий равна 1, т.е.

р₁+ р₂ + р₃ + ... + р_m = 1.

Тогда

Следовательно, задача сводится к взаимно-двойственной задаче линейного программирования.

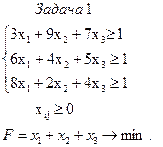
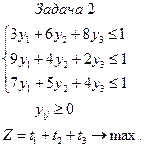
Решая вторую задачу симплекс-методом, получим оптимальное решение:

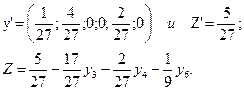
Установим соответствие между переменными:

x₁	x₂	x₃		x₄	x₅	x₆
y₄	y₅	y₆	y₁	y₂	y₃
2/27		1/9			17/27

Тогда оптимальное решение задачи 1:

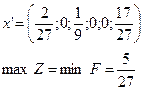
Тогда ;

Вывод: целесообразно выпустить 40% продукции А₁, 60% продукции А₃, а продукцию А₂ не выпускать вообще.

Оптимальную стратегию определим аналогично:

, тогда

q₂ =0, что соответствует отброшенной стратегии В₂

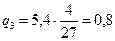
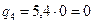
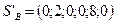
Значит, оптимальным является спрос на 1 и 3 вид продукции соответственно – 20% в состоянии В₁ и 80% в состоянии В₃ .

При решении задачи с использованием элементов игр целесообразно использовать следующий алгоритм:

1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А является стратегии, соответствующие строкам с элементами, заведомо меньшими по сравнению с элементами других строк, для игрока В исключают столбцы, где элементы значительно больше, чем в других столбцах.

2. Определить верхнюю и нижнюю цены игры и проверить, имеется ли седловая точка. Если, то седловая точка есть и соответствующие ей стратегии являются оптимальными и цена будет совпадать с верхней и нижней ценой. Если седловая точка отсутствует, то применяют смешанные стратегии. Для игр размером (m х n) используют симплекс-метод, для игр размером 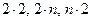возможен геометрический метод решения.