Общая постановка задачи. Принцип оптимальности и управления Беллмана.
Динамическое программирование – это метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на этапы (шаг). Модели динамического программирования применяют при разработке правил управления запасами, принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию, при распределении капитальных вложений между возможными направлениями их использования, при составлении календарных планов текущего и капитального ремонта оборудования и его замены и др. Рассмотрим общую постановку задачи динамического программирования. Пусть в результате управления система S переходит из состояния S0 в состояние Sn. При этом управление этой системой можно разбить на n-шагов, каждый из которых может быть описан уравнением
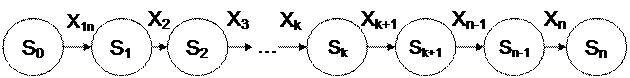
где Хк(к=1,2…n) – управление системой на каждом шаге.
Состояние Sk системы зависит от состояния Sk-1 и эффективности управления на k-том шаге Хк, то есть:
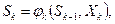 k=1, 2…n – уравнение состояния Sk не зависит от предшествующих состояний.
k=1, 2…n – уравнение состояния Sk не зависит от предшествующих состояний.
Тогда эффективность каждого шага будет выражаться некоторой функцией:
Zk=fk(Sk-1, Xk), k=1,2…n
А эффективность управления системой:
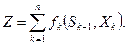
Критерием оптимизации является определение такого допустимого управления Х, переводящего систему S из состояния S0 в состояние Sn, при котором функция Z будет принимать наибольшее (наименьшее) значение.
Таким образом, существуют определенные правила применения методов динамического программирования:
1. оптимизация представляет многошаговый процесс;
2. целевая функция равна сумме целевых функций каждого шага;
3. выбор управления на каждом k-шаге зависит только от состояния системы к этому шагу, а состояние Sk зависит от предшествующего состояния Sk±1 и управления Xk;
4. на каждом шаге управления Xk зависит от конечного числа управляющих переменных, а состояние Sk от конечного числа параметров.
Принцип оптимальности Беллмана
Каково бы ни было состояние S-системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех, оставшихся шагах, включая данный. Следовательно, на каждом шаге любого состояния системы Sk-1 решение Xk нужно выбирать, помнив, что этот выбор влияет на последующее состояние Sk и дальнейший процесс управления, зависящий в дальнейшем от Sk.
Для построения уравнения Беллмана рассмотрим задачу, начиная с последующего шага.

n – шаг
Хn- управление на n-шаге
Согласно принципу оптимальности, Хn выбирают так, чтобы для любых состояний Sn-1 получить максимум целевой Zn' функции на этом шаге. Тогда Zn'(Sn-1) называют условным максимумом целевой функции на n-ом шаге.
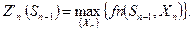
Максимизация осуществляется по всем допустимым значениям Xn. Значения Xn', при котором достигается Zn'(Sn-1), называют условным оптимальным управлением на n-м шаге.
Рассмотрим (n-1) шаг. Для состояния Sn-2 значение целевой функции достигает максимума, если
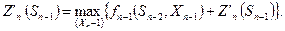
Тогда условий максимум целевой функции, полученной при оптимальном управлении на (n-k+1) шагах, начиная с k-того шага и до конца, определяется:
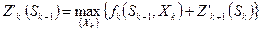 - уравнение Беллмана
- уравнение Беллмана
оптимальное решение задачи динамического программирования
Х'=(Х'1, Х'2, Х'3…. Х'n) – получается из последовательности условных оптимальных управлений на каждом шаге.