Исходные данные

Вид продукции	Производительность работы линии, шт. в сутки	Затраты на работу линии, у.е. в сутки	План, шт

A B C

Составить оптимальный план загрузки оборудования, чтобы затраты были минимальными, а задания выполнено не более чем за 10 суток. Построить экономико-математическую модель затрат.

Задача 2.4.

Фирма производит два популярных безалкогольных напитка, которые может продать в полном объеме. Однако, объем производства ограничен количеством основного инструмента и производственной мощностью имеющегося оборудования. Для производства I л. Напитка «Cola» требуется 0,02 ч. работы оборудования, для производства 1 л «Fanta» - 0,04 часа. Расход специального инструмента соответственно составляет 0,01 кг и 0,04 кг на 1 л. Ежедневное время работы оборудования составляет 24 часа, расход основного ингредиента не может превышать 16 кг в день. Прибыль от реализации 1 л. напитка «Cola» составляет 0,10 у.е.; от реализации напитка «Fanta» 0,30 у.е. Сколько продукции каждого вида целесообразно производить чтобы получить максимальную ежедневную прибыль?

Задача 2.5

Завод - производитель деталей для автомобилей выпускает два различных типа деталей. X и Y. Завод располагает фондом рабочего времени в 4000 чел. - час. в неделю Для производства одной детали типа X требуется 1 чел - час, а для производства одной детали типа Y - 2 чел. - час. Производственные мощности завода позволяют выпускать максимум 2250 деталей типа X, и 1750 деталей типа Y в неделю. Каждая деталь типа X требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа Y необходимо 5 кг металлических стержней и 2 кг листового металла Уровень запаса каждого вида металла составляет 10000 кг в неделю Кроме того, еженедельно завод поставляет 600 деталей типа X своему постоянному заказчику. Существует профсоюзное соглашение, в котором указано, что общее число производимых в течение одной недели деталей должно составлять не менее 1500 штук. Сколько деталей каждого типа целесообразно производить, чтобы максимизировать общий доход за неделю, если доход от производства одной детали типа X составляет 30 у.е., а от производства одной детали типа Y - 40 у.е.?

ТЕМА 3. Симплексный метод оптимизации решений экономических задач

Занятие 2

Экономическая сущность симплекс-метода и область его применения в решении экономических задач.
Методика отыскания оптимального решения.
Двойственные задачи и алгоритм их решения.
Методика решения задач средствами MS Excel

Для решения задач симплекс методом с иcпользованием прикладных программных продуктов наиболее оптимальным является применение табличного процессора MS Excel, при помощи которого задача симплекс-метода решается в табличной форме.

Алгоритм составления симплекс таблиц на примере задачи на максимум:

1. Система ограничений записывается в форме уравнений, введя дополнительные переменные x_n₊_i≥0, i=1,2,…, m.

Уравнение z-c₁x₁-c₂x₂-…-c_nx_n=c₀, полученное переносом всех переменных в левую часть целевой функции, называют оценочным уравнением.

2. Заполняется первая симплексная таблица (см. таблицу 1):

- в первом столбце записываем базисные переменные;

- во втором – свободные члены;

- в третьем и последующих – коэффициенты при переменных x1, x2, …, xn+m;

- в предпоследнем столбце – оценочные отношения;

Таблица1. Заполнение симплекс-таблицы

Базисные переменные	b_i	Коэффициенты	Оценочные отношения
x₁	x₂	…	x_n	x_n+1	x_n+2	…	x_n+m
x_n+1	b₁	a₁₁	a₁₂	…	a_1n			…
x_n+₂	b₂	a₂₁	a₂₂	…	a_2n			…
…	…	…	…	…	…	…	…	…	…
x_n+m	b_m	a_m1	a_m2	…	a_mn			…

Рассмотрим стандартную задачу на распределение ресурсов на примере задачи, разобранной в теоретическом курсе и практической работе №1. Приведем систему ограничений нашей задачи к каноническому виду, введя дополнительные переменные X3, X4, X5, X6:

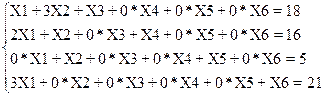
F=2X1+3X2+0*X3+0*X4+0*X5+0*X6

Построим в MS Excel симплекс таблицу, приведенную на рисунке 9.

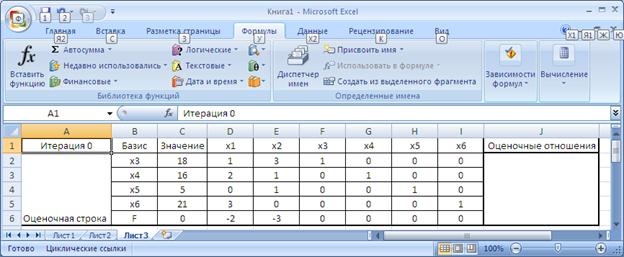
Рисунок 9. Построение первой симплекс таблицы

Данная таблица расположена в диапазоне ячеек А1:J6. В колонку B (B2:B5) запишем перечень наших базисных переменных. Для первого базисного решения такими переменными являются дополнительные переменные X3-X6. В колонку C (C2:C5) запишем правую часть нашей системы уравнений. В колонки D-I (D2:I5) внесем коэффициенты при соответствующих переменных нашей системы уравнений. Последняя строка таблицы (F6:I6) называется оценочной. В нее запишем коэффициенты при соответствующих переменных нашей целевой функции с противоположным знаком.

Если в оценочной строке все числа, начиная с колонки D положительные, то данная итерация дает нам оптимальное решение нашей задачи. Если в оценочной строке имеется хотя бы одно отрицательное число, то решение не оптимальное и имеется возможность отыскать лучшее (не худшее) решение в следующей итерации.

Шаг 1. В оценочной строке выбираем отрицательное число с наибольшим модулем и:

- если в соответствующем столбце имеется хотя бы один положительный коэффициент, то возможен переход к лучшему решению;

- если же все коэффициенты отрицательные, то задача не имеет конечного оптимума.

В нашем случае это колонка E (E2:E6). Выделим ее серым цветом. Это – разрешающая колонка.

Шаг 2.Вычисляем оценочные отношения для каждой строки. Оценочные отношения равны:

- ∞, если b_i ≥ 0, a_ip < 0,

- ∞, если a_ip = 0,

- 0, если b_i = 0, a_ip > 0,

- b_i/a_ip, если b_i ≥ 0, a_ip > 0

Строка, в которой находится минимальное значение оценочного отношения, называется разрешающей строкой. В нашем случае это строка 4. Выделим ее серым цветом, как показано на рисунке 10. Если имеется несколько одинаковых оценочных отношений, то выбираем любое из них.

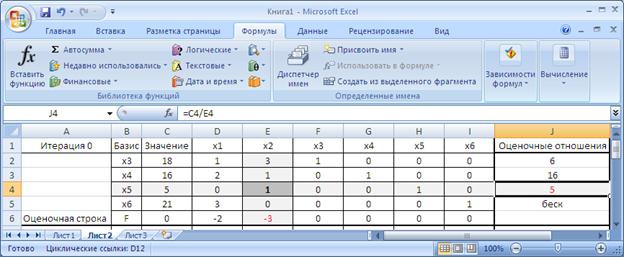
Рисунок 10. Нахождение разрешающей строки, столбца, ячейки

Ячейка на пересечении разрешающей строки и столбца дает нам разрешающий элемент (он обозначается α). Выделим его для наглядности темно-серым цветом.

Шаг 3.Построим вторую симплекс таблицу, аналогичную первой (рис. 11).

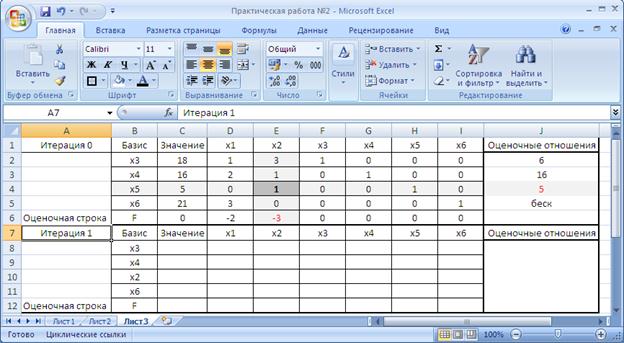
Рисунок 11. Построение второй симплекс таблицы

Заполняем вторую симплекс таблицу:

- определим новый базис – переменную разрешающей строки (в нашем случае переменная X5) заменяем переменной разрешающего столбца (в нашем случае переменная X2), остальные оставляем;

- если α≠1, то все элементы разрешающей строки делим на α, чтобы получить разрешающий элемент, равный 1, и полученную таким образом строку пишем в новой таблице на прежнем месте. В нашем случае разрешающий элемент в ячейке Е4 = 1, таким образом переносим значения ячеек С4:I4 в ячейки С10:I10 (рис.12);

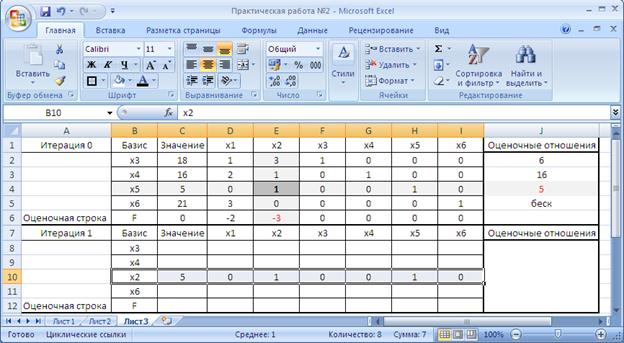
Рисунок 12. Перенос значения разрешающей строки из первой симплекс-таблицы

- нулим разрешающий столбец: к каждой из остальных строк прибавляем вновь полученную строку, умноженную на такое число, чтобы в разрешающем столбце получился 0, полученные строки пишем в новой таблице на тех же местах. В нашей задаче, например значение ячейки С8 будет равно C2+C10*(0-E2)=C2-C10*E2 (рис. 13);

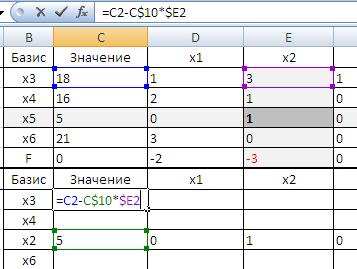
Рисунок 13. Вычисление значения ячеек

- аналогичные значения необходимо скопировать и в остальные ячейки, предварительно корректно зафиксировав необходимые части адреса: =C2-C$10*$E2 (рис. 14).

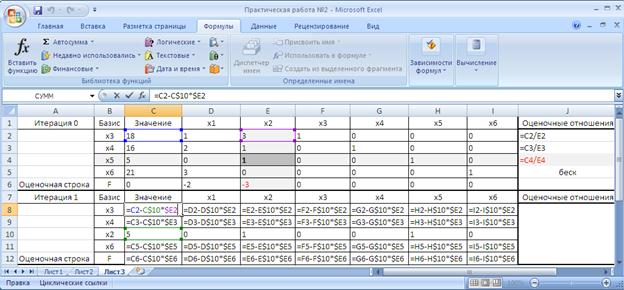
Рисунок 14. Заполнение ячеек второй симплекс таблицы

Шаг 4. Просматриваем оценочную строку:

- если все числа положительны, то решение оптимальное, максимальное значение функции равно свободному члену оценочной строки; а оптимальное решение определяется свободными членами при базисных переменных, все свободные переменные равны 0;

- если в оценочной строке имеется хотя бы один отрицательный элемент, то решение не оптимально, необходимо повторить шаги 1-4.

Для нашей задачи оптимальное решение будет найдено после итерации 3. Финальный вид полученных симплекс-таблиц в формульном виде приведен на рисунке 7, в числовом виде на рисунке 15.

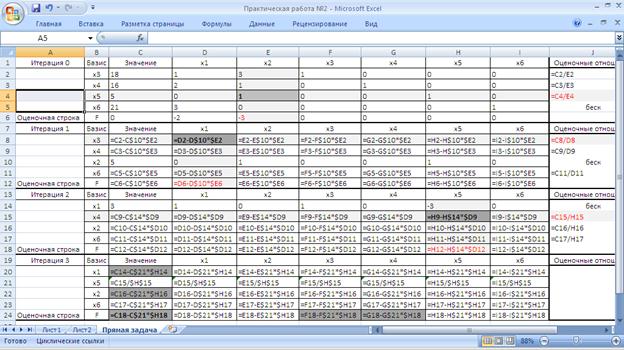
Рисунок 15. Симплекс таблица в формульном виде

Рисунок 16. Симплекс таблица в числовом виде

Видим, что в оценочной строке все элементы положительные, значит оптимальное решение найдено X_опт=(6; 4; 0; 0; 1; 3). Максимальное значение функции равно свободному члену оценочной строки, находящемуся в ячейке С24, Z_max=24. Значения Х1 и Х2, при которых функция принимает максимальное значение равно значению соответствующих свободных членов в столбце C (X1 – C20, X2 – C22). Остаток ресурса с из задачи равен значению свободного члена в ячейке С21, остаток ресурса d из задачи равен значению свободного члена в ячейке С23. Конечный вид целевой функции на после последней итерации F=24-0,8*X3-0,6*X4 → max.