Общая постановка экономической задачи линейного программирования
Метод линейного программирования, используемый для оптимизации экономических решений, относится к экономико-математическим методам, целью которых является построение определенной математической модели и экономический анализ полученного решения.
Под моделью понимают условный образ какого-либо объекта. Экономико-математическая модель есть математическое описание исследуемого экономического процесса или объекта.
Выделяют три основных этапа проведения экономико-математического моделирования:
1. Постановка цели и задач исследования, качественное описание объекта.
2. Формирование математической модели изучаемого объекта, выбор методов исследования, подготовка исходной информации.
3. Анализ математической модели, обработка и анализ результатов.
При использовании экономико-математических методов производят сравнение многочисленных вариантов экономических и управленческих решений. В результате отбирают оптимальный вариант.
Для осуществления общей постановки задачи линейного программирования рассмотрим наиболее типичные частные задачи.
Задача об использовании ресурсов
Условие: Для изготовления двух видов продукции А и В используют четыре видов ресурсов – а, в, с, d. Прибыль, получаемая от реализации единицы продукции А – 2 рубля, продукции В – 3 рубля. Размеры запасов и нормы расхода каждого вида ресурсов приведены в таблице.
| Вид ресурса | Запас ресурса | Норма расходов ресурсов на единицу продукции | |
| A | B | ||
| a | |||
| b | |||
| c | - | ||
| d | - |
Цель задачи: построить оптимальный план производства продукции А и В, при котором прибыль была бы максимальной.
Решение:
Пусть x1 и x2 - объем выпуска продукции А и В соответственно. Тогда для производства заданного объема продукции потребуется затратить следующее количество различных ресурсов:
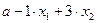 единиц,
единиц,
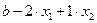 единиц,
единиц,
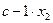 единиц,
единиц,
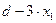 единиц.
единиц.
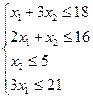 Потребление ресурсов не может превышать их запасов, тогда составим систему неравенств по ограничениям ресурсов:
Потребление ресурсов не может превышать их запасов, тогда составим систему неравенств по ограничениям ресурсов:
Объемы производства продукции А и В должны быть больше или равны 0, значит x1 ≥ 0 и x2 ≥ 0.
Суммарная прибыль составит:
F=2x1+3x2 → max
Задачу легко обобщить на случай выпуска n-видов продукции с использованием m-видов ресурсов (ресурсы могут быть, как материальными, так и стоимостными).
Пусть:
хj , где j = 1, 2,.…, n – число единиц продукции, запланированной к производству;
bi где i=1,2…m – запас ресурса Si;
aij - число единиц ресурса Si в ед.продукции Pj;
cj - прибыль от реализации единицы продукции Pj,
Тогда задача оптимизации плана производства примет следующий вид:
 |
при условии, что x1 ≥ 0, x2 ≥ 0, x3 ≥ 0,..., xn ≥ 0 , при котором функция F примет максимальное значение:
F=c1x1+c2x2+…+cnxn → max
Задача о составлении рациона
Условие: Имеется два вида продукта питания, содержащих витамины (питательные вещества) S1, S2, S3. Стоимость 1 кг продуктов соответственно 4 и 6 руб.
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором количество питательных веществ было бы не ниже нормы.
| Питательное вещество | Норма пит. вещества | Число единиц питательных веществ в 1кг продукта | |
| A | B | ||
| S1 | |||
| S2 | |||
| S3 |
Решение:
Пусть x1 и x2 – соответственно объем потребления продуктов А и В в дневном рационе. Тогда дневной рацион будет составлять из следующего количества питательных веществ:

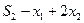
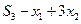
Составим систему ограничений дневного рациона с точки зрения нормы потребления питательных веществ:

при x1 ≥ 0, x2 ≥ 0
Общая стоимость рациона составит
F=4x1+6x2 → min
Для общей постановки задачи (например, для определения потребительской корзины) построим следующую модель, где:
xj (j=1, 2…n) - число единиц продукции j - вида;
bi (i=1, 2…m) – минимум содержания в рационе питательного вещества Si;
aij – число единиц питательного вещества Si в единице продукции j –того вида;
сj – стоимость единицы j – того вида продукции.
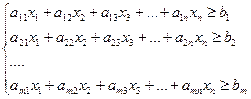 Тогда
Тогда
При условии x1 ≥ 0, x2 ≥ 0, x3 ≥ 0,..., xn ≥ 0
Функция принимает минимальное значение:
F=c1x1+c2x2+…+cnxn → min
Задача об использовании производственной мощности,
или о загрузке оборудования
Условие: фирме необходимо за время Т выпустить n единиц продукции Р1, Р2, Р3..Рn. Задействовано оборудование S1,S2,...,Sm. Производительность единицы оборудования aij, затраты на изготовление единицы продукции Рj в единицу времени на станке Si составит bij.
Цель: определить оптимальный план загрузки оборудования так, чтобы денежные затраты на производство продукции были бы минимальными.
Решение:
Пусть xij – время изготовления продукции Рj на станке Si. Время работы каждого вида оборудования не должно превышать Т, тогда
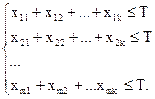
План выпуска по видам продукции составит
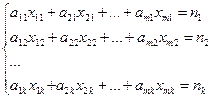
при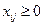 , где i = 1, 2…k
, где i = 1, 2…k
Тогда затраты на производство всей продукции составят:
F=b11x11+b12x12+…+bmkxmk → min
Задача об оптимальном раскрое (использовании) материалов
Условие: На раскрой поступает материал в количестве a единиц. Требуется изготовить L разных деталей, пропорциональных числам b1, b2,...,bi (условие комплектности). Каждая деталь может быть раскроена n-различными способами, причем при каждом i-том способе (i=1, 2…n) может быть получено aik единиц k-той детали (k=1, 2 … L). Найти план раскроя, обеспечивающий максимальное число комплектов.
Решение:
Пусть xi – число единиц материала, раскраиваемых i - тым способом, x - число раскраиваемых деталей. Весь материал a раскраивается i -тым способом, тогда
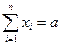 |
Тогда требуемое количество деталей выразится:
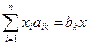 |
при xi ≥ 0 (i=1, 2 … n)
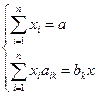 По условию нужно найти решение X = (x1, x2,...,xn), удовлетворяющее системе уравнений
По условию нужно найти решение X = (x1, x2,...,xn), удовлетворяющее системе уравнений
при условии, что xi ≥ 0, при котором функция F=X примет максимальное значение.
Если раскраивается m - различных материалов, тогда каждый j -тый вид материала (j=1, 2 … m) может быть раскроен n-способами, где каждый i -тый способ (i=1, 2 … n) дает aik единиц k -того изделия (k=1, 2…l), а запас j -того материала равен aj единиц и xij - число единиц j -того материала, раскраиваемого i -тым способом.
Тогда экономико-математическая модель примет следующий вид:
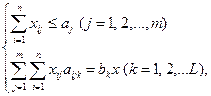 |
при xij ≥ 0 функция F = X примет максимальное значение.
Рассмотренные выше традиционные примеры позволяют сформулировать общую задачу линейного программирования: дана система m -линейных уравнений и неравенств с n -переменными.

Найти такое решение системы X = (x1, x2,...,xj ,...,xn ), где xi ≥ 0, при котором функция
F = c1x1+c2x2+…+cnxn → max(min)
или
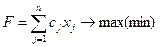 |
Если система ограничений состоит из неравенств, то задача линейного программированияназывается стандартной. Если система ограничений состоит из уравнений, то задача называется канонической. В совместном случае задачу называютобщей.
Для решения задачи линейного программирования применяют вспомогательную теорему, позволяющую привести стандартную задачу к канонической.
| ТЕОРЕМА Всякому решению (a1, a2,…,an) неравенства ai1x1+ai2x2+…+ainxn ≤ bi coответствует решение (a1, a2,…, an, an+1) уравнения ai1x1+ai2x2+…+ainxn +xn+1=bi , в котором xn+1 ≥ 0. И наоборот, каждому решению уравнения соответствует определенное решение неравенства. |
Тогда, если в системе ограничений имеется знак «≤», то дополнительная переменная вводится со знаком « + », если в ограничении знак «≥0 », то дополнительная переменная вводится со знаком « - ».
Тогда в общей постановке задачи линейного программирования система ограничений примет следующий вид:
 |
где xj ≥ 0 (j=1, 2 … n) и функция
F=c1x1+c2x2+…+cnxn → max(min).