МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ ОБСЛУЖИВАНИЯ
Результаты обслуживания заявок зависят, прежде всего, от соотношения между числом абонентом S и числом обслуживающих приборов V телефонной станции.
Если выполняется условие S<V, то это означает, что для любого абонента всегда найдется свободный ОП (канал обслуживания). По экономическим соображениям обслуживание такого рода находит весьма ограниченное применение. Оно целесообразно лишь для малых групп абонентов, передача сообщений которых должна осуществляться незамедлительно.
На практике, как правило, выполняется условие S>V, что определяет следующую классификацию КС (как СМО) по способу обслуживания.
1. Система обслуживания с потерями, когда в ситуации занятия всех приборов поступающая заявка получает отказ и выбывает из системы.
2. Система обслуживания с ожиданием при ограниченной или неограниченной длине очереди. Вызов, поступающий в такую систему в момент, когда в ней имеется хотя бы один свободный ОП, обслуживается немедленно. В противном случае заявка ставится в очередь. При ограничении длины очереди или ограничении времени ожидания обслуживания заявка может либо выбывать из системы, либо возвращаться в нее через какое-то время. В этом смысле очередь в телефонии можно рассматривать как источник повторных вызовов.
Определим состояния, в которых может находиться КС как СМО:
Хо - состояние, когда все ОП свободны;
Хi при i=1...V - состояние, когда заняты ровно i приборов;
Хv+m - состояние, когда занято V приборов и m>1 заявок находится в очереди.
Процесс, протекающий в системе, состоит в том, что в любой случайный момент времени система скачком переходит из одного состояния в другое в результате появления нового вызова, освобождения прибора или ухода заявки из очереди. В системе, таким образом, протекает случайный процесс с непрерывным временем.
Обозначим Рк(t) как вероятность того, что в произвольно взятый момент времени t система находится в состоянии Хк.
Можно утверждать, что в соответствии с выражением полной вероятности событий
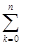 Рк(t) = 1,
Рк(t) = 1,
где n - число возможных состояний системы.
Будем полагать, что переход из состояния в состояние обусловлен либо входным потоком заявок, когда приход новой заявки переводит систему из состояния Xi в состояние Хi+1, либо потоком покидающих систему заявок (потоком освобождений), когда уходящая из системы заявка изменяет состояние Хi на состояние Xi-1. Иными словами, переходы из одного состояния системы в другое являются обратимыми.
Таким образом, если в момент времени t система находится в состоянии Хi, то на малом интервале времени dt возможными являются переходы только в три состояния:
1. Xi(t) – Xi-1(t+dt);
2. Xi(t) - Xi(t+dt);
3. Xi(t) – Xi+1(t+dt).
Это ограничение позволяет значительно упростить процесс поиска решения и, в то же время, достаточно адекватно отражает реальные процессы, протекающие в КС.
Модель КС (телефонной станции) как СМО для принятых ограничений удобно представить графом состояний, изображенном на рис. 7.1.
Переход из состояния Xi в Xi+1 происходит с интенсивностью 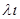 , а переход из состояния Xi+1 в Xi состояние - с интенсивностью
, а переход из состояния Xi+1 в Xi состояние - с интенсивностью  I+1. Закругленные замкнутые) стрелки, направленные из состояния Xi в него же, означают, что система может не только перейти в соседние состояния, но и остаться в прежнем.
I+1. Закругленные замкнутые) стрелки, направленные из состояния Xi в него же, означают, что система может не только перейти в соседние состояния, но и остаться в прежнем.
Для системы с конечным числом состояний n существует установившийся (стационарный) режим работы, для которого существуют конечные вероятности состояний, то есть для t 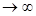 вероятности состояний равны Рi=lim Рi(t) при t
вероятности состояний равны Рi=lim Рi(t) при t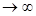 , где i=0,...,n, а сумма Pi по-прежнему равна единице. Для стационарного режима работы СМО, очевидно, должно действовать правило равенства входящих и исходящих потоков в каждом состоянии системы:
, где i=0,...,n, а сумма Pi по-прежнему равна единице. Для стационарного режима работы СМО, очевидно, должно действовать правило равенства входящих и исходящих потоков в каждом состоянии системы:
1. интенсивность перехода в состояние Хк равна 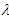 k-1P k-1 +
k-1P k-1 +  k+1P k+1;
k+1P k+1;
2. интенсивность перехода из состояния Хк равна 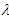 kP k +
kP k +  kP k.
kP k.
В состоянии равновесия эти два потока должны быть равны, что может быть представлено в математической форме равенством или уравнением вида:
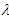 k-1P k-1 +
k-1P k-1 +  k+1P k+11 =(
k+1P k+11 =(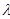 k +
k +  k )P k.
k )P k.
Данное выражение называется в теории телетрафика основным уравнением для СМО.
Частная задача, связанная с отдельными уравнениями при к=0 и к=n, может быть решена, если полагать, что l i-1 = l i-2 = l i-3 = … = 0;  0 =
0 =  i-1 =
i-1 =  i-2 = … = 0;
i-2 = … = 0;  n+1 =
n+1 =  n+2 = … = 0; ln = ln+1 = … = 0.
n+2 = … = 0; ln = ln+1 = … = 0.
Тогда для к=0 получаем li -1 Pi –1 +  1P 1 = (lо +
1P 1 = (lо + о)Ро, следовательно,
о)Ро, следовательно,
Р1 = 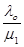 Ро,
Ро,
При к=1 lо Ро +  2P2 =(l1+
2P2 =(l1+ 1 )P 1,
1 )P 1,
P 2 = 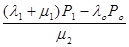 =
= 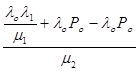 =
= 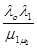 Ро.
Ро.
Приведенные равенства позволяют получить и записать общее решение основного уравнения телетрафика для СМО в виде:
P к = 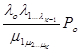 ;
;
Ро + Р1 + Р2 + … + Рn = 1;
Ро + Ро 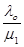 + Ро
+ Ро 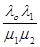 + … + Ро
+ … + Ро 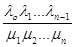 = 1;
= 1;
Ро = 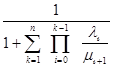 .
.
Полученное решение для определения вероятности произвольного k-го состояния системы является основополагающим равенством элементарной теории массового обслуживания, используемым для анализа эффективности функционирования СМО.