Замена переменных в тройном интеграле.

Пусть в тройном интеграле 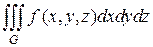прямоугольные координаты 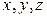преобразуются к новым координатам 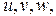которые связаны с 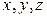соотношениями

(1.21)

которые однозначно разрешимы относительно :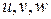

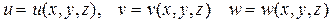. (1.22)

Обозначим через область в пространстве 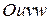, в которую отобра-жается область пространства с помощью формул (1.22).

Если функции (1.21) имеют в области непрерывные частные произ-водные первого порядка и якобиан преобразования

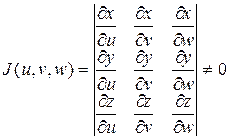
в области , то ограниченная замкнутая область 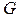пространства взаимно однозначно отображается на область пространства 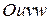и для тройного интеграла имеет место следующая формула замены переменных:

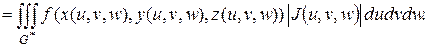(1.23)

Цилиндрические координаты 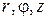связаны с прямоугольными координатами 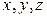соотношениями:

(1.24)

где 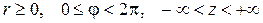(рисунок 1.10).

Рисунок 1.10

Рисунок 1.11

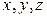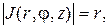При переходе от прямоугольных координат к цилиндрическим координатам по формулам (1.24) поэтому формула (1.23) принимает вид

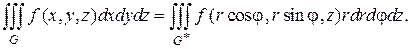
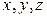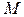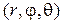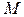Если точка в пространстве имеет прямоугольные координаты , то сферическими координатами точки называют тройку чисел , где ― расстояние от точки до начала координат 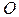, 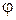― угол между лучом (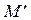― проекция точки 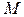на плоскость ) и осью , ― угол между положительным направлением оси 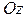и лучом (рисунок 1.11).

Связь между прямоугольными и сферическими координатами определяется соотношениями 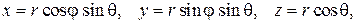где При этом 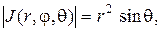и формула (1.23) принимает вид

Обобщенными сферическими координатами называют переменные , связанные с прямоугольными координатами 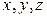формулами

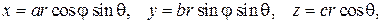
где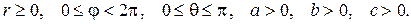

Для обобщенных сферических координат 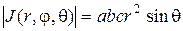и формула (1.23) имеет вид