Условия устойчивости

Любая система будет устойчивой, если переходные процессы, вызванные внешними воздействиями, с течением времени будут затухать.

Поведение любой системы математически записывается в виде:

(6.1)

,

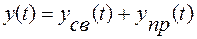где 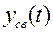– свободная составляющая выходной координаты, которая характеризует переходной процесс,

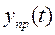– принужденная составляющая выходной координаты, которая характеризует закон изменения выходной координаты после окончания переходного процесса. Другими словами данная составляющая определяет поведение системы при приложении возмущающих воздействий.

Свободная составляющая находится по формуле:

(6.2)

(6.2)

,

где 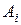- коэффициент, зависящий от начальных условий,

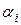- действительная часть корней характеристического уравнения [1],

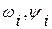- соответственно мнимая часть корней характеристического уравнения и начальная фаза, определяемая из начальных условий.

Из уравнения (6.2) следует, что система будет устойчивая, если все действительные составляющие корней характеристического уравнения будут отрицательными. Если хотя бы один действительный корень будет положительным, то соответствующая экспонента будет с течением времени бесконечно возрастать.

Исходя из этого предположения, русским ученым Ляпуновым были сформулированы следующие основные теоремы устойчивости.

Теорема 1. Если все действительные составляющие корней характеристического уравнения математической модели САУ отрицательные, то реальная система будет устойчивой, и никакие малые неучтенные параметры не изменят устойчивости системы.

Теорема 2. Если хотя бы одна действительная составляющая корней характеристического уравнения математической модели САУ будет положительной (при прочих отрицательных), то реальная система будет неустойчивой, и никакие малые неучтенные параметры не приведут систему к устойчивости.

Теорема 3.Если хотя бы одна действительная часть корней характеристического уравнения математической модели САУ будет нулевой при прочих отрицательных, то реальная система будет находиться на границе устойчивости (система нейтральная), и любые малые неучтенные параметры могут сделать систему как устойчивой, так и неустойчивой.

Таким образом, для определения устойчивости необходимо определить только знак действительных составляющих корней характеристического уравнения системы, не вычисляя полного значения корней уравнения.

Решение данной задачи упрощается, используя частотные методы анализа характеристического уравнения.