Принцип аргумента

Определение устойчивости частотными методами основан на вспомогательной теореме, известной как принцип аргумента.

Пусть характеристическое уравнение системы имеет следующий вид и найдены корни этого уравнения:

(6.3)

,

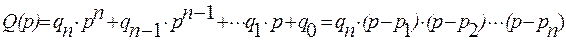где 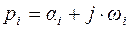- корни характеристического уравнения Q(p) = 0.

 

Амплитудная и фазочастотная характеристика характеристического уравнения запишется в виде:

(6.4)

(6.3)

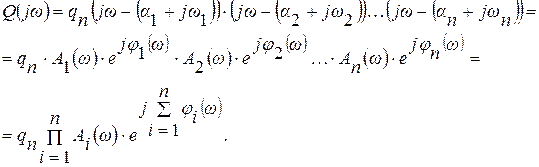
При изменении частоты изменяется и амплитуда и фаза. Определим, как изменяется фаза, при изменении частоты от - ∞ до + ∞.

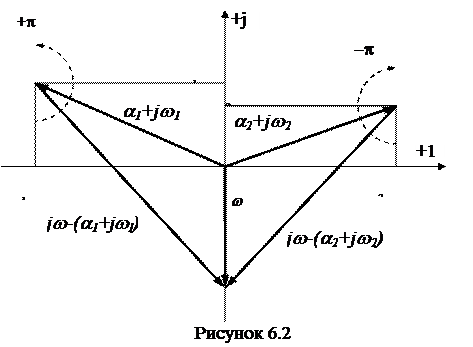
Пусть один из корней имеет отрицательную действительную часть (например 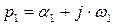). Вектор этого корня в комплексной плоскости расположен слева от мнимой оси (в левой полуплоскости) (рисунок 6.2).

При изменении частоты от - ∞ до + ∞ вектор 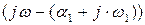будет скользить по мнимой оси и повернется против часовой стрелки (в положительном направлении) на угол плюс π радиан.

 

(6.4)

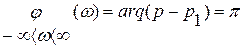. (6.3)

 

Если таких корней будет «k» и фаза каждого вектора повернется на угол π, то результирующий вектор повернется против часовой стрелки на угол k×π радиан.

Пусть один из корней имеет положительную действительную часть (например 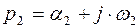). Вектор этого корня в комплексной плоскости расположен справа от мнимой оси (в правой полуплоскости) (рисунок 6.2).

При изменении частоты от - ∞ до + ∞ вектор 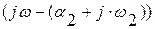будет скользить по мнимой оси и повернется по часовой стрелки (в отрицательном

(6.5)

направлении) на угол -π радиан.

Если таких корней будет «l» и фаза каждого вектора повернется на угол -π, то результирующий вектор повернется по часовой стрелки на угол -l×π радиан.

 

 

Таким образом, фаза характеристического уравнения при изменении частоты от - ∞ до + ∞ повернется угол «k×π - l×π» радиан. Учитывая, что

(6.6)

n = k+l,

получается:

 

(6.7)

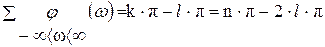. (6.4)

 

Если диапазон изменения частоты уменьшить в 2 раза, то:

 

(6.8)

. (6.5)

 

Итак, принцип аргумента можно сформулировать так:

Аргумент (фаза) характеристического уравнения при изменении частоты от 0 до ∞ изменяется на угол «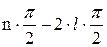» радиан.