Математический аппарат

Поведение САУ в общем случае описывается системой нелинейных дифференциальных уравнений, при решении которых вводится ряд допущений, либо применяются различные методы линеаризации, решаемые с помощью численных методов.

Пусть некоторая система автоматического регулирования описывается линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами:

(3.1)

где b_i, a_i – коэффициенты уравнения,

x, y – входной и выходной сигналы соответственно.

Данное уравнение является однородным уравнением с правой частью. Если коэффициенты b_i, a_i постоянные, то САУ является линейной, в противном случае - нелинейной. Решением данного уравнения является выражение вида:

y(t)=y_св(t)+y_пр(t), (3.2)

где y_св(t) - свободная составляющая выходной координаты, которая является решением уравнения (3.1) без правой части:

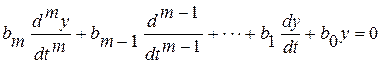, (3.3)

y_пр(t) - принужденная составляющая выходной координаты, которая является частным решением уравнения (3.1) и зависит от закона изменения внешних воздействий х(t) или f(t).

Примеры математического описания различных объектов широко представлены в рекомендованной литературе.

Порядок уравнений динамики САУ зависит от сложности процессов, протекающих в нем, и от принятых допущений. Если же снизить порядок не удается, то существует прием, называемым методом разделения движения, который существенно упрощает расчет и проектирование систем управления. Если в САУ есть движения, не сопоставимые по времени протекания (медленные и быстрые процессы), то тогда систему можно разделить на две системы. Каждая из них описывают поведение САУ, но в различных масштабах времени.

Самым главным инструментом при изучении поведения САУ является преобразование Лапласа, которое переводят оригиналы функции и сигналов в их изображения.

Оператор Лапласа переводит дифференциальные уравнения из временной области в частотную. В этой области оперировать дифференциальными уравнениями проще, так как изображение всех переменных, независимо от формы и порядка дифференцирования представлены одинаково, как функции оператора «p». При этом решение сводится к решению алгебраических уравнений.

Если оригиналf(t) представляет собой функцию времени t, то изображениеэтой функции F(p) есть функция комплексной переменной p, задаваемой в виде следующего интеграла:

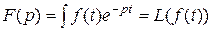. (3.4)

Если в уравнении (3.3) заменить оператор дифференцирования на оператор Лапласа, то это уравнение можно записать таким выражением:

B(p)×Y(p)=A(p)×X(p), (3.5)

где A(p)=a_npⁿ+a_n-1p^n-1+…+a₁p+a₀;

B(p)=b_npⁿ+b_n-1p^n-1+…+b₁p+b₀; (3.6)

 

Из уравнения (3.5):

. (3.7)

Переход от изображения Y(p) к оригиналу y(t) осуществляется с помощью обратного преобразования Лапласа:

. (3.8)

Если знаменатель уравнения (3.8) не имеет кратных корней, то оригинал y(t) находится по известной из курса математики формуле разложения:

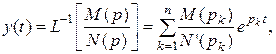(3.9)

где M(p) - многочлен числителя,

N(p) - многочлен знаменателя,

N¢(p) - производная знаменателя,

p_k -корни характеристического уравненияN(p)=0.