Векторы и действия над ними

Любой вектор можно представить как где - единичный вектор (орт), а A - абсолютное значение вектора . Орты, соответствующие направлениям осей декартовой системы координат, будем обозначать . Таким образом, в проекциях на эти оси вектор имеет следующий вид:

. (1.1)

Проекции вектора на оси координат называются также его компонентами, или составляющими вектора.

Сложение в векторной алгебре понимается как алгебраическое сложение компонент векторов:

. (1.2)

Умножение вектора на число (скаляр) m есть получение вектора

(1.3)

с новым абсолютным значением |m|A.

Скалярное произведение векторов обозначается и определяется следующим образом:

, (1.4)

где - угол между направлениями векторов. В результате скалярного произведения векторов образуется число. Как видно из (1.4), значение скалярного произведения может быть равным нулю при равных нулю исходных векторах (т.е. векторах с нулевыми значениями A и B), либо при нулевых значениях . В последнем случае эти векторы называются ортогональными: они направлены под прямым углом друг к другу.

Векторное произведение векторов , обозначаемое есть

, (1.5)

где 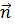- единичный вектор, направленный по нормали к плоскости векторов , причем так, что образуют «правую тройку» векторов: если смотреть вдоль , то кратчайшее угловое расстояние между векторами А и В, обозначенное φ, будет соответствовать движению от по часовой стрелке. Удобно записывать векторное произведение в форме следующего определителя:

(1.5a)

раскрытие которого приводит к указанному результату. Векторное произведение некоммутативно, т.е. сомножители нельзя переставлять местами, имея в виду сохранение результата. А именно:

. (1.6)

Под векторно-скалярным (смешанным) произведением векторов понимается скаляр ; при этом

, (1.7).

т. е. важен циклический порядок следования перемножаемых векторов , при сохранении которого безразлично, какие два вектора из трёх образуют векторное произведение. На основании (1.4) и (1.5) легко установить, что

(1.8)

Далее, запишем формулу двойного векторного произведения:

(1.9)

1.2. Линейное преобразование векторов

Вернёмся к вопросу обумножении вектора на скаляр. Согласно (1.3), равенство векторов

(1.10)

равносильно трем скалярным равенствам:

, (1.10а)

Если m - положительное число, то векторы направлены одинаково, а при отрицательном m - противоположно («параллельно» и «антипараллельно»); говорят, что такие векторы коллинеарны. Мы имеем здесь дело с частным видом линейного преобразования набора компонент в аналогичный набор ; заметим, что эти совокупности компонент, вполне определяющие векторы , мы также можем называть векторами.

В общем случае под однородным линейным преобразованиемрассматриваемых векторов понимают сопоставление вектору нового вектора , компоненты которого определяются по формулам:

, (1.11)

где т_хх, т_ху,..., т_zу, т_zz - некоторые числа. Векторы , компоненты которых связаны соотношениями (1.11), уже не коллинеарны; следовательно, записанное преобразование определяет не только изменение абсолютного значения («растяжение» или «сжатие») вектора, но и некоторый его поворот.

Остановимся на формальном описании преобразования (1.11). С точки зрения линейной алгебры, таблица чисел

(1.12)

образует матрицу, а равенства (1.11)выражают операцию умножения матрицы на вектор-столбец (), приводящую к вектору-столбцу (В_х, В_у, B_z). В частности, в (1.10а) мы имеем случай, когда |, где

(1.13)

так называемая единичная матрица.

Вместо символа матрицы введём иной символ и запишем равенства (1.11) в следующей сокращённой форме:

(1.14)

Умножение на здесь понимается как выполнение операций над компонентами вектора , содержащимися в. (1.11). Соотношение (1.14) есть обобщение равенства векторной алгебры (1.10), в котором роль множителя вместо скаляpa m играет объект более сложного характера , называемый тензором. В частности, единичной матрице I соответствует также обозначаемый единичный тензор I.

Тензор выступает как оператор, который, действуя на вектор , преобразует его в другой вектор .

 

1.3. Радиус-вектор

Рассмотрим важный пример вектора, зависящего от точки пространства, в которой он рассматривается, т. е. пример векторной функции. Это радиус-вектор,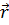

, (1.15)

который представляет собой направленный отрезок, соединяющий начало координат О (0, 0, 0) с некоторой «текущей» точкой М(х, у, z). Длина радиус-вектора r = ОМ (его абсолютное значение) есть скалярная функция

. (1.15а)

Очевидно, отрезок, соединяющий две точки Р(х', у', z') и М(х, у, z), изображается разностью их радиус-векторов:

. (1.16)

Абсолютное значение этого вектора выражает расстояние между точками Р и М:

(1.16a)