Понятие устойчивости системы.
Рассмотрим некоторую систему, динамика которой описывается линейным (или линеаризованным) дифференциальным уравнением:
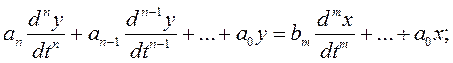 (1)
(1)
Это уравнение описывает изменение выходной величины y(t) во времени при переменном входном воздействии x(t).
Если входное воздействие отсутствует, или устранено (x=0 при t≥0), то уравнение (1) описывает «свободное движение» системы:
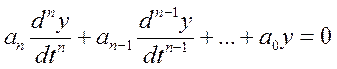 (2)
(2)
Решение уравнения (2) существует и может быть представлено в виде:
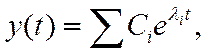 (3)
(3)
где: Сi – постоянные, определяемые начальными условиями. (Уравнение 2 –nго порядка требует задания n начальных условий и имеет n постоянных).
λi – корни так называемого характеристического уравнения:
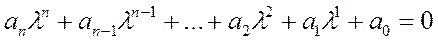 (4)
(4)
Алгебраическое уравнение nой степени имеет n корней (λ1, λ2… λi… λn). – в общем случае – комплексных.
Итак, для того чтобы решить дифференциальное уравнение (2) – т.е. определить функцию y(t), необходимо решить алгебраическое характеристическое уравнение (4), т.е. определить корни λ1 … λi… λn.
Решение уравнения (2), т.е. выражение (3) определяет поведение переменной y во времени, т.е. её свободное движение после устранения возмущения может быть сложным:
|
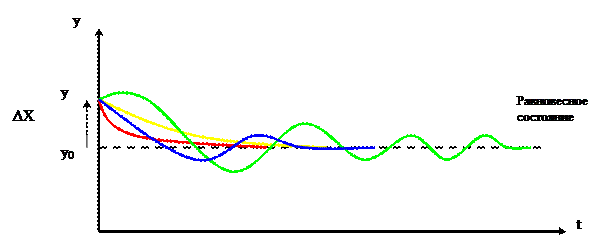

Если при t→∞ y(t)→y(0) т.е. к равномерному состоянию, то система является устойчивой; в противном случае – не устойчивой (тогда говорят, система пошла в разнос).
Характер изменения функции y(t) во времени зависит от корней [λ1 … λi… λn].
 Действительно, если мы рассмотрим простейшую степенную функцию
Действительно, если мы рассмотрим простейшую степенную функцию
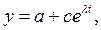
т.о. если, λ<0., функция y – убывающая: y→a т.е. эта простейшая система устойчива.

если λ>0., – y неограниченно возрастает, т.е. система не устойчива.

Анализируя более сложную степенную зависимость (3) можно сделать вывод, что устойчивость системы определяется корнями λ1 … λi… λn.
Теорема Ляпунова: [ условие устойчивости Ляпунова]:
«Чтобы система была устойчивой, необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения были отрицательными».
Система не устойчива, если действительная часть, хотя бы одного из корней (λ1 … λi… λn) положительна.
Таким образом, определение устойчивости системы сводится к выяснению условий, при которых все корни характеристического уравнения имеют отрицательные действительные части, т.е. все корни располагались в левой полуплоскости комплексной плоскости.
