Метод исследования устойчивости А.М. Ляпунова.
Ляпунов разработал два общих метода исследования нелинейных систем. Однако первый метод применим только для исследования устойчивости в малом линеаризуемых систем. Рассмотрим подробнее второй метод Ляпунова.
Второй метод Ляпунова, называемый также прямым методом, дает достаточные условия устойчивости, то есть определяет часть области устойчивости. Идея метода наглядно объясняется с помощью метода фазового пространства.
Рассмотрим в фазовом пространстве замкнутую поверхность произвольной формы, описываемую уравнением:
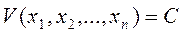 (17)
(17)
Где V – функция координат 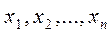 , а С – параметр, определяющий величину функции. Каждому его значению соответствует определенная поверхность. С уменьшением С поверхность сжимается так, что поверхность, соответствующая меньшему С, находится целиком внутри поверхностей с большими значениями С. Если движение изображающей точки М происходит только внутрь поверхности, то этот факт может считаться достаточным признаком устойчивости системы, так как в этом случае все фазовые траектории неизбежно придут к началу координат.
, а С – параметр, определяющий величину функции. Каждому его значению соответствует определенная поверхность. С уменьшением С поверхность сжимается так, что поверхность, соответствующая меньшему С, находится целиком внутри поверхностей с большими значениями С. Если движение изображающей точки М происходит только внутрь поверхности, то этот факт может считаться достаточным признаком устойчивости системы, так как в этом случае все фазовые траектории неизбежно придут к началу координат.
При таком характере движения изображающей точки производная
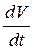 функции
функции 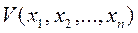 должна быть отрицательна.
должна быть отрицательна.
Пользуясь терминологией Ляпунова можно сформулировать следующее достаточное условие устойчивости:
если можно подобрать такую знакоопределенную функцию 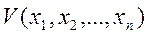 , производная которой по времени
, производная которой по времени 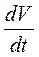 , согласно дифференциальным уравнениям системы, тоже является знакоопределенной функцией, но противоположного знака, то возмущенное движение асимптотически устойчиво.
, согласно дифференциальным уравнениям системы, тоже является знакоопределенной функцией, но противоположного знака, то возмущенное движение асимптотически устойчиво.
Знакоопределенной называется функция, которая при всех значениях переменных имеет один знак, а в начале координат обращается в нуль. Например,
 ,
,
где а, b, с – постоянные положительные коэффициенты.
В случае, если производная  обращается в нуль вне начала координат, получаем неасимптотическую устойчивость возмущенного движения системы. Графически это значит, что изображающая точка может застрять на определенной поверхности, где
обращается в нуль вне начала координат, получаем неасимптотическую устойчивость возмущенного движения системы. Графически это значит, что изображающая точка может застрять на определенной поверхности, где 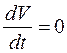 , не дойдя до начала координат.
, не дойдя до начала координат.
Таким образом, суть прямого метода Ляпунова состоит в отыскании для исследуемой нелинейной системы функции V, удовлетворяющей выше указанному требованию. Такие функции называются функциями Ляпунова.
Преимущество метода Ляпунова заключается в том, что для определения знака производной вдоль фазовых траекторий не требуется решать дифференциальное уравнение динамики системы. Необходимо только представить его в форме Коши.
Применение прямого метода Ляпунова на практике осложнено двумя обстоятельствами:
- достаточным характером утверждений (т.е. если условия метода не выполняются, то об устойчивости положения равновесия ничего сказать нельзя, можно только порекомендовать подобрать другую функцию Ляпунова);
- отсутствием общих рекомендаций по выбору функций Ляпунова.
Рассмотрим пример исследования системы второго порядка прямым методом Ляпунова. Пусть динамика системы описывается системой дифференциальных уравнений в форме Коши:
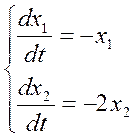
Для исследования устойчивости по методу Ляпунова необходимо подобрать знакоопределенную функцию V второго порядка. Пусть она имеет вид:

Найдем ее производную

Сравним полученное выражение с нулем. Как видно, при любых не равных нулю значениях 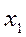 и
и  производная
производная  . При
. При 
 . Следовательно, исследуемая система асимптотически устойчива.
. Следовательно, исследуемая система асимптотически устойчива.