Сущность метода наименьших квадратов

Метод наименьших квадратов (МНК) получил широкое распространение при обработке экспериментальных данных в целях исследования различных функциональных зависимостей, определения параметров распределений и т.д.

Существует широкий класс задач, в которых МНК является оптимальным методом обработки данных. В других классах задач использование МНК часто оправдывается алгоритмической простотой его реализации ценой небольших потерь в оптимальности получаемого результата. Для нелинейных задач статистического анализа данных зачастую невозможно использование каких-либо других методов, кроме МНК.

Эти и другие причины объясняют широкое распространение МНК при статистическом анализе экспериментальных данных, в частности, при выявлении функциональных зависимостей. Исторически МНК возник значительно раньше других методов обработки данных. Вероятностное обоснование МНК дано К. Гауссом в начале XIX в. и А.А. Марковым в начале XX в.

Предположим, что требуется определить компоненты вектора

A_<k> = (a₁, a₂,…, a_k)^т,

который в общем случае не поддаётся непосредственному наблюдению. Однако можно наблюдать вектор

Y_<n> = ( y₁, y₂,…, y_n)^т,

функционально связанный с искомым вектором A_<k>:

Y_<n> = F_<n>(t; A_<k>). (8.2.1)

При этом соотношение размерностей векторов A и Y может быть произвольным. В частном случае A может быть скалярной величиной, а Y – вектором, и наоборот.

В общем случае вектор-функция F является нелинейной. Схема оценивания, в которой по наблюдениям в некоторые моменты времени t_i, 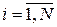одного набора параметров (в данном случае компонентов вектора Y) необходимо оценить компоненты другого набора параметров (компоненты вектора A), функционально связанного с первым, называется схемой косвенных наблюдений.

Процесс наблюдения всегда сопровождается ошибками. Наблюдаемое значение функции (8.2.1) в момент времени t_i отклоняется от теоретического вследствие случайных факторов. Следовательно, результат наблюдения всегда представляет собой реализацию случайной величины. В общем случае ошибка наблюдения нелинейным образом связана с наблюдаемой функцией.

На практике часто удаётся путём линеаризации уравнений модели (8.2.1) относительно случайных ошибок свести уравнения к форме, когда случайные ошибки входят аддитивно или мультипликативно (см. §1.1). Однако наиболее простым и самым распространённым типом связи ошибок наблюдения и наблюдаемых величин является линейная аддитивная связь, когда модель наблюдения может быть представлена уравнениями

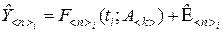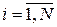, , (8.2.2)

где 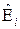– вектор аддитивной ошибки в i-й момент наблюдения.

В дальнейшем будем рассматривать эту схему наблюдения. Уравнения типа (8.2.2) называются уравнениями наблюдения. Поскольку компоненты вектора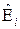являются случайными неизвестными наблюдателю величинами, то для поиска оценок вектора A_<k> используется уравнение вида

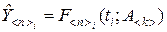, (8.2.3)

которое может оказаться и несовместным, поскольку отражает наблюдаемый процесс приближённо. Поэтому уравнение (8.2.3) принято называть условным.

Если моменты времени t_i, 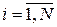представляют собой известные и в данной задаче фиксированные величины, то фактически вектор-функция F является функцией только вектора A. Поэтому в дальнейшем в число аргументов будем включать моменты времени t_i тогда, когда они либо неизвестны, либо известны с ошибкой. С учётом сказанного уравнение наблюдения запишется в виде

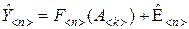. (8.2.4)

В соответствии с методом наименьших квадратов оценки компонентов вектора A отыскиваются на основе минимизации суммы квадратов отклонений между Y и F:

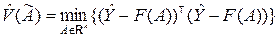, (8.2.5)

где 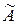– вектор, представляющий собой решение задачи (8.2.5); R^k – k- мерное вещественное пространство.

Часто вместо минимизации квадратичной функции (8.2.5) для оценивания вектора A используют минимизацию квадратичной функции более общего вида:

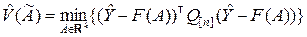, (8.2.6)

где Q_[n] – неотрицательно определённая симметричная матрица, которая называется весовой.

Очевидно, что задача (8.2.5) является частным случаем задачи (8.2.6), если в качестве весовой выбрать единичную матрицу.

Показатель качества оценивания (8.2.5) в скалярной форме имеет вид

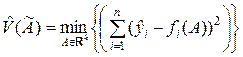, (8.2.7)

где 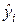и f_i, 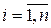– компоненты вектора Y и вектор-функции F соответственно.

Скалярная форма показателя (8.2.6):

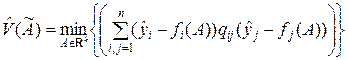, (8.2.8)

Для сокращения записей, а также упрощения некоторых выкладок в последующем будем использовать в основном векторно-матричную запись показателя качества оценивания вектора A.

Необходимое условие минимума функции (8.2.5) или (8.2.6) состоит в том, что её частные производные по всем компонентам a_i вектора A должны быть равны нулю:

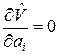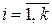, . (8.2.9)

Развёрнутый вид условий (8.2.9) в скалярной форме представляется следующей системой уравнений:

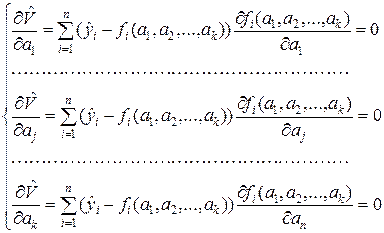(8.2.10)

Система уравнений (8.2.10) в теории МНК называется системой нормальных уравнений. Её решение, т.е. вектор 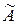будем в дальнейшем называть МНК-оценкой.

П р и м е р 8.1. Требуется оценить скалярную величину a, для которой уравнение наблюдения имеет вид

, .

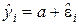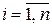▼ Предположим, что оценку параметра a необходимо отыскивать минимизацией суммы квадратов отклонений

.

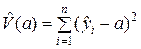Тогда необходимое условие минимума этой суммы квадратов в соответствии с (8.2.9) запишется в виде

.

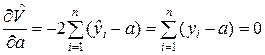Оценка искомой величины

.

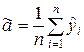Следует заметить, что при решении данной задачи обоснование выбора функции V(a) отсутствовало, хотя ранее в § 2.4 указывалось, что оптимальный выбор данной функции диктуется условиями задачи.

Замечание приведено в связи с тем, что в дальнейшем будет даваться и иное решение этой же задачи. ▲

В общем случае система нормальных уравнений нелинейная относительно искомых параметров, а искомые параметры – компоненты вектора A – выражаются нелинейным образом через компоненты вектора наблюдения .