Нормальные уравнения и оценки наименьших квадратов

Для линейной модели наблюдения (8.3.1) квадратичная функция (8.2.6), при минимизации которой отыскиваются оценки компонентов вектора A, будет иметь вид

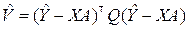, (8.3.9)

а нормальные уравнения (8.2.9) – вид

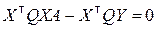. (8.3.10)

Можно показать, что система нормальных уравнений (8.3.10) всегда совместна [10]. Будем считать, что матрица X имеет ранг k (предполагается, что n ³ k), а матрица весов Q – невырожденная. Тогда матрица 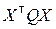будет невырожденной, а потому из равенства (8.3.10) можно получить выражение для оценки вектора A:

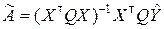. (8.3.11)

Если весовая матрица единичная (Q = E), то вместо соотношения (8.3.11) получим равенство

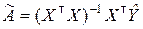. (8.3.12)

Если относительно вектора ошибок ничего не известно, то ничего нельзя сказать и о свойствах оценок (8.3.11) или (8.3.12). Если же соотношение (8.3.2) выполняется, то оценки (8.3.11), (8.3.12) являются несмещёнными. Действительно

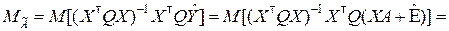
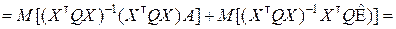
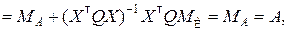
поскольку 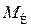= 0.

Пусть корреляционная матрица вектора ошибок наблюдений имеет вид (8.3.4). Вычислим корреляционную матрицу вектора оценок 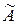. Обозначим

; .

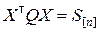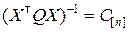В этих обозначениях формула для МНК-оценки (8.3.11) перепишется в виде

,

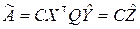где .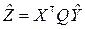

Тогда корреляционная матрица вектора оценок 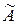вычисляется по формуле

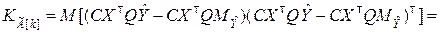
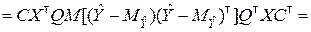(8.3.13)

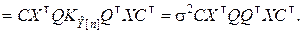
В процессе преобразований в выражении (8.3.13) учтено, что

, .

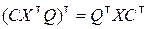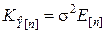Если Q = E, то

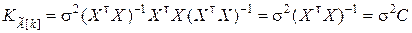. (8.3.14)

На практике наиболее часто используется вариант МНК-оценивания, при котором в качестве весовой матрицы Q выбирается матрица 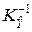, поскольку в таком случае МНК-оценка получается эффективной. Доказательство этого факта можно найти, например, в [10]. Для такого варианта корреляционная матрица оценки вычисляется по формуле

,

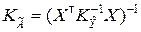которая при 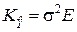совпадает с выражением (8.3.14).

Когда величина s² известна, формулы (8.3.13), (8.3.14) позволяют отыскать корреляционную матрицу вектора 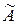. Из данных формул следует, что даже при некоррелированных равноточных наблюдениях компоненты вектора оценок оказываются коррелированными. Для их некоррелированности необходима ещё ортогональность столбцов матрицы наблюдений X (при Q = E) или столбцов матрицы в общем случае.

Если дисперсия наблюдений s² неизвестна, её необходимо оценить наряду с компонентами вектора A, иначе невозможно отыскать корреляционную матрицу вектора 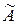, которая даёт характеристики точности оценивания.

Покажем, каким образом можно получить оценку величины s². В математической статистике доказывается, что остаточная сумма квадратов

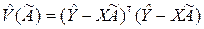(8.3.15)

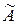(– МНК-оценка при линейной модели наблюдения) имеет закон распределения 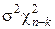, если вектор ошибок наблюдения 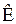характеризуется корреляционной матрицей s²E (n – размерность вектора , k – число оцениваемых параметров).

В скалярной форме выражение (8.3.15) имеет вид

.

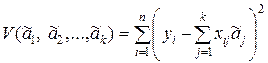На основании свойств 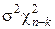- распределения получается, что

,

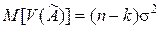а потому оценку для величины s² можно приближённо вычислять по формуле

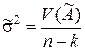. (8.3.16)

Отметим, что это оценка несмещённая.

Без доказательства укажем, что МНК-оценки не всегда получаются эффективными. Ранее уже отмечалось со ссылкой на работу [10], что свойством эффективности обладают МНК-оценки для моделей наблюдения (8.3.3), (8.3.4) при Q = E, (8.3.3), (8.3.5) при Q = G^–1 и (8.3.3), (8.3.8) при Q = R^–1. Это следует, в частности, для нормального распределения вектора ошибок 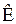из эффективности оценок, получаемых по методу максимального правдоподобия, поскольку МНК и ММП-оценки совпадают при указанном способе выбора весовых матриц. При всех остальных способах выбора матрицы весов МНК-оценки неэффективны. Однако это не означает, что варианты выбора матрицы весов Q, приводящие к неэффективным оценкам, нецелесообразны. Различные соображения могут привести к выбору матрицы весов в другой форме.

П р и м е р 8.2. Известно, что величина a – постоянная, схема оценивания имеет вид

, ,

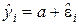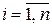где 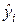– наблюдаемая величина, 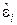– ошибка наблюдения. Требуется по результатам наблюдения определить оценку величины a с использованием МНК, а также получить характеристики точности оценивания при известных моментных характеристиках ошибки :

, , .

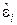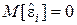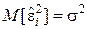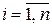Данная задача совпадает с задачей из примера 8.1, однако там ничего не говорилось о статистических свойствах ошибок измерения .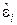

▼ Случайную величину 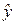представим в виде вектора

.

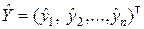Роль вектора оцениваемых параметров играет скалярная величина a, т.е. k = 1. Поэтому матрица X, имеющая размерность n´k, представляет собой вектор-столбец, состоящий из единиц:

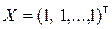
В качестве матрицы весов Q выбираем единичную матрицу E_[n]. МНК-оценку скалярной величины a вычисляем по формуле (8.3.12). Предварительно найдём матрицы 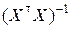и :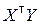

;

;

.

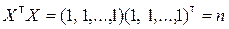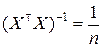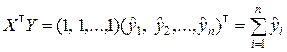Окончательно получим

.

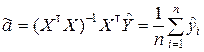Заметим, что решение совпадает с полученным в примере 8.1.

Эта оценка является несмещённой и эффективной. Определим точность оценки 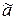. На основании формулы (8.3.14) получим

,

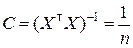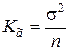. (8.3.17)

Если бы величина s² не была априори известной, то её оценку можно было бы получить на основании формулы (8.3.16):

.

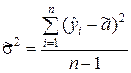Затем можно найти дисперсию оценки 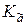по формуле (8.3.17) с заменой s² на .

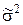Данный пример фактически указывает, каким образом следует оценивать математическое ожидание случайной величины и каковы при этом точечные характеристики этих оценок. Напомним, что ранее тот же результат для оценки математического ожидания был получен с помощью предельных теорем.

▲

П р и м е р 8.3. Рассмотрим задачу, аналогичную приведённой в примере 8.2, с тем отличием, что независимые измерения величины a производятся с различной от эксперимента к эксперименту точностью, которая характеризуется дисперсией , .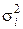

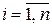▼ Итак, имеем схему неравноточных наблюдений:

; ; .

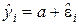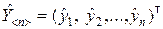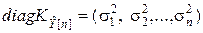Корреляционная матрица 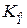взята в диагональной форму в силу независимости измерений.

Данную задачу сводим к предыдущей, используя преобразования (8.3.6), (8.3.7). При этом

,

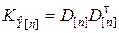где D – диагональная матрица с диагональю

.

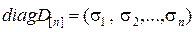Тогда формула (8.3.7) приводит к новому вектору

.

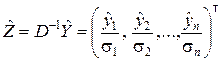Легко убедиться, что корреляционная матрица вектора 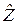получается при этом единичной, а задача сводится к предыдущей. Уравнение (8.3.3) записывается в виде

,

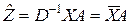где .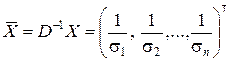

Далее находим, как и в примере 8.2:

; ; ;

.

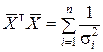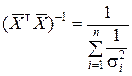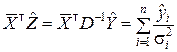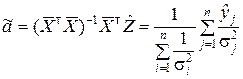Данная оценка является несмещённой и эффективной, причём

.

▲

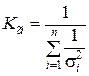Сравнивая полученное решение с решением задачи 8.1 или 8.2, видим, что учёт неравноточности измерений приводит к иному решению. Возвращаясь к замечанию, указанному в примере 8.1, можно опять же подчеркнуть, что учёт статистических свойств ошибок измерений приводит к необходимости иного выбора функции V(a), чем это было сделано в примере 8.1 или 8.2.