рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Потенциальная энергия упруго деформированного стержня равна
Реферат Курсовая Конспект
Потенциальная энергия упруго деформированного стержня равна
Потенциальная энергия упруго деформированного стержня равна - раздел Образование, Уфа 2008 ...
 , (8.14)
, (8.14)
где  – объем стержня.
– объем стержня.
Отношение энергии 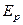 к тому объему
к тому объему  , в котором она заключена, называется плотностью энергии u. Тогда
, в котором она заключена, называется плотностью энергии u. Тогда 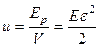 – плотность энергии упругой деформации при растяжении (или сжатии).
– плотность энергии упругой деформации при растяжении (или сжатии).
Аналогично нетрудно получить, что плотность энергии деформации при сдвиге равна  .
.
6. Кручение
Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.
Возьмем однородную проволоку, верхний конец ее закрепим, а к нижнему концу приложим закручивающие силы. Они создадут вращающий момент относительно продольной оси проволоки. При этом каждый радиус нижнего основания повернется вокруг продольной оси на угол  . Такая деформация называется кручением. Закон Гука для деформации кручения имеет вид
. Такая деформация называется кручением. Закон Гука для деформации кручения имеет вид
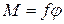 , (8.15)
, (8.15)
где  – модуль кручения, постоянная для данной проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.
– модуль кручения, постоянная для данной проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.
Выведем выражение для модуля кручения.
Пусть имеется цилиндрическая трубка радиуса  . Причем толщина ее
. Причем толщина ее очень мала по сравнению с радиусом. Площадь сечения трубки равна
очень мала по сравнению с радиусом. Площадь сечения трубки равна  . Обозначим через
. Обозначим через 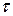 касательное напряжение в том же основании. Тогда момент сил, действующий на это основание, будет
касательное напряжение в том же основании. Тогда момент сил, действующий на это основание, будет 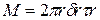 . При закручивании совершается работа
. При закручивании совершается работа  .
.
Разделим ее на объем трубки  . Найдем плотность упругой энергии при деформации кручения
. Найдем плотность упругой энергии при деформации кручения
 (8.16)
(8.16)
Найдем эту же величину иначе.
Мысленно вырежем из трубки бесконечно короткую часть (рис.8.5).

| Рис. 8.5 |
В результате кручения бесконечно малый элемент трубки ABDC перейдет в положение  . Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге равна
. Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге равна
 (8.17)
(8.17)
Приравнивая его выражению (8.16), находим искомое соотношение
 (8.18)
(8.18)
Если стенка трубки имеет конечную толщину, то модуль  найдется интегрированием последнего выражения по
найдется интегрированием последнего выражения по 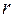 . Это дает
. Это дает  где
где  – внутренний радиус трубки,
– внутренний радиус трубки,  – внешний радиус трубки.
– внешний радиус трубки.
Для сплошной проволоки радиуса 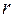 модуль кручения
модуль кручения 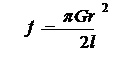 .
.
Контрольные вопросы
1. Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.
2. Какова физическая сущность упругих сил?
3. Сформулируйте закон Гука? Когда он справедлив?
4. Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?
5. Что такое упругий гистерезис и упругое последействие?
6. Каков физический смысл модуля Юнга и модуля сдвига?
7. Что такое упругое последействие?
8. Выведите выражения для деформаций при всестороннем растяжении.
9. Что называется коэффициентом Пуассона?
10. Определите энергию деформированного тела.
11. Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.
12. Какой вид имеет закон Гука при кручении.
13. Выведите выражение для модуля кручения.
Лекция №9. Механика жидкостей и газов
При изучении движения жидкостей и газов рассматривают сплошную непрерывную среду, не вдаваясь в их молекулярное строение. В такой постановке механика жидкостей и газов является разделом механики сплошных сред. Она охватывает гидростатику, гидродинамику, газовую динамику, теорию упругости и т.д.
1. Механические свойства жидкостей и газов
Как показывает опыт, при движении одного слоя жидкости или газа относительно другого вдоль поверхности их соприкосновения действуют силы, которые называются силами внутреннего трения. Величина этих сил зависит от относительной скорости слоев и стремится к нулю при ее уменьшении. Эти силы действуют только при движении жидкостей и газов, значит, в рассматриваемых в настоящем разделе средах сдвинуть один слой относительно другого (т.е. вызвать деформацию сдвига) можно ничтожными силами. Поэтому жидкие тела не имеют определенной формы и принимают форму сосуда, в котором они находятся.
Экспериментально также установлено, что изменение объема жидкости и газа, помещенных в сосуд под поршнем, вызывается действием сил на жидкость или газ со стороны поршня. Следовательно, в отношении деформации растяжения-сжатия жидкости и газы ведут себя как упругие тела. На практике газы и жидкости подвергаются лишь всестороннему сжатию. В специальных же условиях жидкость может быть подвергнута и растяжению. Газ всегда находится в сжатом состоянии, и при отсутствии внешних сил всегда стремится увеличить свой объем до бесконечности.
Жидкости и газы отличаются в сжимаемости. Газы легко сжимаются, а жидкости практически не сжимаемы. В тех случаях, когда сжимаемость не существенна, механические свойства жидкостей и газов можно считать одинаковыми.
2. Гидростатика
Гидростатика изучает поведение жидкости и газа в состоянии покоя. Она характеризуется понятием давления и двумя законами: законом Паскаля и законом Архимеда. Рассмотрим их.
Упругость жидкости или газа определяется степенью их сжатия и характеризуется силой, действующей отдельными частями жидкости или газа друг на друга или на внешние тела. Сила в расчете на единицу поверхности называется давлением.
Мысленно разделим жидкость на две части некоторой поверхностью S и выберем на этой поверхности небольшую площадку с площадью ∆S (рис.9.1).
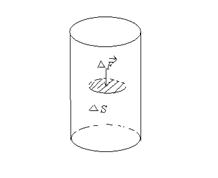
| Рис.9.1 |
Жидкость, находящаяся по одну сторону площадки, действует на жидкость, находящуюся по другую сторону, некоторой силой 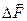 . В неподвижной жидкости в касательном направлении к границе раздела двух слоев силы не действуют. Поэтому сила
. В неподвижной жидкости в касательном направлении к границе раздела двух слоев силы не действуют. Поэтому сила  направлена перпендикулярно к площадке. Отношение величины
направлена перпендикулярно к площадке. Отношение величины  этой силы к площади ∆S площадки, на которую сила действует, определяет среднее давление жидкости в том месте, где находится площадка. Если размеры площадки устремить к нулю, то мы получим давление p в данной точке жидкости, т.е.
этой силы к площади ∆S площадки, на которую сила действует, определяет среднее давление жидкости в том месте, где находится площадка. Если размеры площадки устремить к нулю, то мы получим давление p в данной точке жидкости, т.е.
 (9.1)
(9.1)
Можно показать, что в покоящейся жидкости или газе на одном уровне давление одинаково во всем объеме (закон Паскаля).
Выделим в жидкости вертикальный цилиндр высотой h, образующая которого параллельна силе тяжести, и площадью сечения ∆S . Силы, действующие на образующие этого объема, равны, так как жидкость покоится. На торцевые стороны поверхности цилиндра действуют силы  и
и 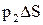 , внутри него – объемная сила
, внутри него – объемная сила  . Так как жидкость покоится, то силы, действующие на нижнее основание цилиндра сверху и снизу, должны быть одинаковы:
. Так как жидкость покоится, то силы, действующие на нижнее основание цилиндра сверху и снизу, должны быть одинаковы:  где
где  – плотность жидкости.
– плотность жидкости.
 , (9.2)
, (9.2)
т.е. разность давлений на верхнее и нижнее основание цилиндра равна гидростатическому давлению столба жидкости между этими основаниями.
Пусть теперь цилиндр заполнен другой жидкостью, но не смешивающейся с жидкостью в сосуде или каким-нибудь твердым телом. Предположим, что плотность введенного твердого или жидкого тела равна  . Силы, действующие на основания по-прежнему равны
. Силы, действующие на основания по-прежнему равны  и
и 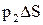 , но
, но  или
или  где
где  – вес введенного тела.
– вес введенного тела.
Кажущийся вес тела 
Но  – вес, например, воды в объеме тела. Поэтому кажущийся вес тела есть
– вес, например, воды в объеме тела. Поэтому кажущийся вес тела есть 
 . Следовательно, погруженное в жидкость тело теряет в своем весе столько, сколько весит вытесненная им жидкость или выталкивающая сила равна весу жидкости, вытесненной телом и направленной вертикально вверх (Закон Архимеда).
. Следовательно, погруженное в жидкость тело теряет в своем весе столько, сколько весит вытесненная им жидкость или выталкивающая сила равна весу жидкости, вытесненной телом и направленной вертикально вверх (Закон Архимеда).
Если 
 , то тело тонет. Если
, то тело тонет. Если 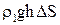 <
< (погруженное тело легче воды), то оно всплывает.
(погруженное тело легче воды), то оно всплывает.
3.Гидродинамика
Гидродинамика представляет собой раздел механики сплошных сред, в котором изучается движение несжимаемых жидкостей и взаимодействие несжимаемых жидкостей с твердыми телами. Жидкость, плотность которой всюду одинакова и изменяться не может, называется несжимаемой.Например,при повышении давления от 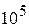 до
до 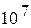 Па плотность воды увеличивается всего лишь на 0,5 %. В случаях, когда силы внутреннего трения при движении жидкости малы по сравнению с другими действующими на неё силами, жидкость практически можно считать невязкой. Воображаемая жидкость, совершенно не обладающая вязкостью, называется идеальной. Например, при температуре выше 0єС многие реальные жидкости (эфир, ацетон, спирт, вода, ртуть) обладают малой вязкостью и потому их можно рассматривать как идеальные жидкости.
Па плотность воды увеличивается всего лишь на 0,5 %. В случаях, когда силы внутреннего трения при движении жидкости малы по сравнению с другими действующими на неё силами, жидкость практически можно считать невязкой. Воображаемая жидкость, совершенно не обладающая вязкостью, называется идеальной. Например, при температуре выше 0єС многие реальные жидкости (эфир, ацетон, спирт, вода, ртуть) обладают малой вязкостью и потому их можно рассматривать как идеальные жидкости.
4. Описание движения жидкостей.
Уравнение неразрывности струи
Возможны два способа описания движения жидкостей. Первый способ заключается в указании положений и скоростей всех частиц жидкости для каждого момента времени. Такой способ описания разрабатывался французским математиком и механиком Жозеф Луи Лагранжем (1736-1813) и называется способом Лагранжа. Однако проще следить не за частицами жидкости, а за отдельными точками пространства и отмечать скорость, с которой проходят через каждую точку отдельные частицы жидкости. При таком способе движение жидкости характеризуется совокупностью функций скорости  , определенных для всех точек пространства. Этот способ называется методом Эйлера (Леонард Эйлер (1707-1783) – математик, механик, физик и астроном, по происхождению швейцарец, в 1727-1741 гг., 1766-1783 гг. жил и работал в России).
, определенных для всех точек пространства. Этот способ называется методом Эйлера (Леонард Эйлер (1707-1783) – математик, механик, физик и астроном, по происхождению швейцарец, в 1727-1741 гг., 1766-1783 гг. жил и работал в России).
Совокупность векторов  , заданных для всех точек пространства, образует так называемое поле вектора скорости. Это поле можно изобразить с помощью линий тока.Линии тока проводят так, чтобы густота их была пропорциональна модулю скорости в данном месте. Тогда по картине линий тока можно судить и о направлении, и о модуле вектора
, заданных для всех точек пространства, образует так называемое поле вектора скорости. Это поле можно изобразить с помощью линий тока.Линии тока проводят так, чтобы густота их была пропорциональна модулю скорости в данном месте. Тогда по картине линий тока можно судить и о направлении, и о модуле вектора  в разных точках пространства: там, где скорость больше, линии тока будут гуще и, наоборот, где скорость меньше, линии тока будут реже (рис.9.2). Например, в точке А густота линий, а следовательно и модуль скорости больше, чем в точке В.
в разных точках пространства: там, где скорость больше, линии тока будут гуще и, наоборот, где скорость меньше, линии тока будут реже (рис.9.2). Например, в точке А густота линий, а следовательно и модуль скорости больше, чем в точке В.

|
| Рис.9.2. Линии тока проводятся так, чтобы вектор скорости в каждой точке пространства был направлен по касательной к соответствующей линии |
Модуль и направление вектора  в каждой точке могут меняться со временем. Поэтому и картина линий тока может непрерывно меняться. Если вектор скорости в каждой точке пространства остается постоянным, то течение называется установившимся или стационарным (или установившимся).При стационарном течении:
в каждой точке могут меняться со временем. Поэтому и картина линий тока может непрерывно меняться. Если вектор скорости в каждой точке пространства остается постоянным, то течение называется установившимся или стационарным (или установившимся).При стационарном течении:
– любая частица жидкости проходит данную точку пространства с одним тем же значением скорости;
– картина линий тока остается неизменным;
– линии тока совпадают с траекториями частиц.
Часть жидкости, ограниченная линиями тока, называется трубкой тока.Вектор  касается поверхности трубки тока в каждой её точке. Следовательно, частицы жидкости во время движения не пересекают стенок трубки тока.
касается поверхности трубки тока в каждой её точке. Следовательно, частицы жидкости во время движения не пересекают стенок трубки тока.
Рассмотрим установившееся движение идеальной несжимаемой жидкости. Выделим в трубке тока две перпендикулярные скорости сечения:  (где скорость течения равна
(где скорость течения равна 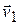 ) и
) и  (где скорость течения равна
(где скорость течения равна  ) (рис.9.3).
) (рис.9.3).

| Рис.9.3 |
Так как жидкость несжимаема, то за одно и то же время через эти сечения пройдут равные объемы жидкости, а следовательно, и одинаковые массы жидкости: , где
, где 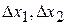 – перемещения сечений
– перемещения сечений  , или
, или 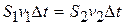 ,т.е.
,т.е. 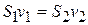 .
.
Так как это равенство справедливо для любой пары произвольно взятых сечений, имеем
 (9.4)
(9.4)
Следовательно, для несжимаемой жидкости при стационарном течении произведение площади поперечной трубки на скорость течения жидкости в любом сечении трубки тока есть величина постоянная.
Соотношение (9.4) называется уравнением неразрывности струи.Оно справедливо и к реальным жидкостям, и даже к газам в том случае, когда их сжимаемостью можно пренебречь. Это уравнение показывает, что:
– в меньших сечениях, где скорость больше, и линии тока будут гуще;
– при изменяющемся сечении трубки тока частицы несжимаемой жидкости движутся с ускорением.
Формула (9.4) справедлива и для всякой реальной трубы, для русла реки и т.п. Например, скорость течения на узких участках речного русла больше, чем на широких и глубоких; скорость воды в струе, вырывающейся из брандспойта, больше, чем в шланге и т.п.
5. Уравнение Бернулли
Рассмотрим наклонную трубку переменного сечения (или реальную трубу), по которой движется идеальная несжимаемая жидкость в направлении справа налево. Мысленно выделим область трубки, ограниченную сечениями, и в которых скорости течения равны соответственно  и
и  (рис. 9.5). Пусть
(рис. 9.5). Пусть  и
и 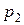 – давления, оказываемые на сечения жидкостью вне элемента,
– давления, оказываемые на сечения жидкостью вне элемента,  и
и  – отмеряемые от некоторого горизонтального уровня высоты, на которых находятся сечения,
– отмеряемые от некоторого горизонтального уровня высоты, на которых находятся сечения, 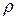 – плотность жидкости.
– плотность жидкости.

|
Рис. 9.4
Определим изменение полной энергии, происходящее в выделенной области за малый промежуток времени  .
.
Полная энергия выделенного элемента трубки складывается из кинетической энергии и из потенциальной энергии, обусловленной силами тяжести. При течении жидкости эта энергия изменяется. Согласно закону сохранения энергии изменение энергии рассматриваемого элемента должно быть равно работе внешних сил, действующих на этот элемент.
За малый промежуток времени  рассматриваемый элемент жидкости 1-2 переместится по трубке. Его границы займут положения 1ґ и 2ґ. Сечение 1 переместится на расстояние
рассматриваемый элемент жидкости 1-2 переместится по трубке. Его границы займут положения 1ґ и 2ґ. Сечение 1 переместится на расстояние  , сечение 2 – на расстояние
, сечение 2 – на расстояние  . Так как поток стационарный, то энергия части элемента между сечениями 1ґ и 2ґ остается неизменной. Объем жидкости, прошедший за время
. Так как поток стационарный, то энергия части элемента между сечениями 1ґ и 2ґ остается неизменной. Объем жидкости, прошедший за время  через сечение 1, равен
через сечение 1, равен  Масса этой части жидкости
Масса этой части жидкости 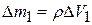 . Аналогично, часть жидкости, находящаяся между сечениями 2 и 2ґ, имеет объем
. Аналогично, часть жидкости, находящаяся между сечениями 2 и 2ґ, имеет объем  и массу
и массу  . Согласно уравнению неразрывности
. Согласно уравнению неразрывности  и, в случае несжимаемой жидкости,
и, в случае несжимаемой жидкости, 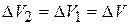 .
.
Потенциальная энергия частиц жидкости, находящаяся между сечениями 1 и 1ґ, равна  .
.
Кинетическая энергия этих частиц  .
.
Аналогично, потенциальная и кинетическая энергии частиц жидкости, находящиеся между сечениями 2 и 2ґ, равны 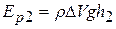 и
и  .
.
Тогда изменение полной энергии всего рассматриваемого элемента жидкости будет
 (9.5)
(9.5)
Силы давления на стенки трубки тока перпендикулярны в каждой точке направлению перемещения жидкости, вследствие чего работы не совершают.
В соответствии с законом сохранения энергии, найденная величина энергии должна равняться работе внешних сил (давления) по перемещению массы  :
:
 (9.6)
(9.6)
Определим эту работу. Внешняя сила  давления совершает работу
давления совершает работу  по перемещению втекающей массы на пути
по перемещению втекающей массы на пути  , в то же время вытекающая масса совершает работу
, в то же время вытекающая масса совершает работу  против внешней силы давления
против внешней силы давления  на пути
на пути  . Поэтому искомая работа
. Поэтому искомая работа  .
.
Так как  , имеем
, имеем
 (9.7)
(9.7)
Приравнивая выражения (9.5) и (9.7), сокращая на 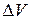 и перенося члены с одинаковыми индексами в одну часть равенства, получим
и перенося члены с одинаковыми индексами в одну часть равенства, получим
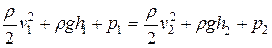 (9.8)
(9.8)
Так как сечения 1 и 2 были выбраны произвольно, то для любого сечения данной трубки тока должно быть
 (9.9)
(9.9)
Это уравнение называется уравнением Бернулли(выведено в 1738 г.) для стационарного течения идеальной несжимаемой жидкости.
Первое слагаемое левой части этого уравнения представляет собой удельную кинетическую энергию жидкости, второе – удельную потенциальную энергию жидкости в поле силы тяжести, третье – удельную энергию жидкости, обусловленную силами давления. Следовательно, уравнение Бернулли выражает закон сохранения энергии (удельной) и формулируется так:
при установившемся движении идеальной несжимаемой жидкости сумма удельной энергии давления и кинетической и потенциальной удельных энергий остается постоянной величиной на любом поперечном сечении потока.
Как видно из уравнения (9.9), все члены его левой части можно рассматривать как величины давления. Величину  называют статическим давлением, величину
называют статическим давлением, величину  – динамическим давлением, величину
– динамическим давлением, величину 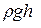 – гидравлическим давлением. Следовательно, уравнению Бернулли можно дать ещё такую формулировку:
– гидравлическим давлением. Следовательно, уравнению Бернулли можно дать ещё такую формулировку:
в установившемся потоке идеальной несжимаемой жидкости полное давление, слагающееся из динамического, гидравлического и статического давлений, постоянно на любом поперечном сечении потока.
Уравнение Бернулли является одним из основных законов механики движения жидкостей и газов, имеющим большое прикладное значение. Приведем несколько примеров.
1. Пусть скорости частиц жидкости в сечениях 1 и 2 трубки тока равны между собой. Тогда из уравнений (9.9) следует, что для этих сечений 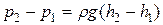 , т.е. разность давлений как и в покоящейся жидкости определяется разностью высот.
, т.е. разность давлений как и в покоящейся жидкости определяется разностью высот.
2. Для горизонтальной трубки тока уравнение Бернулли принимает вид:  .
.
Из уравнений Бернулли и неразрывности следует, что в местах сужения трубопровода скорость течения жидкости возрастает, а давление понижается.
Поток воздуха проходит по трубке с переменным сечением. У открытого широкого конца трубки давление выходящего воздуха становится равным атмосферному. В более узких сечениях давление меньше атмосферного. Поэтому жидкость из сосуда движется по вертикальной трубке. Это явление используется в водо- и пароструйных насосах, пульверизаторах, опрыскивателях сельскохозяйственных растений, ингаляторе и других распылителях жидкости и устройствах.
3. Гидротурбина работает за счет большого давления жидкости (но имеющего малую скорость), падающего по суживающемуся трубопроводу через сопло на лопатки рабочего колеса. При этом потенциальная энергия давления воды переходит в узком трубопроводе и сопле в кинетическую энергию, за счет которой рабочее колесо приводится во вращение.
Аналогичным образом работает и газотурбина.
4. Гидротаран. Вода движется от плотины по наклонному трубопроводу. В конце трубопровода имеется подвижная заслонка, которая может периодически быстро перекрывать трубопровод.
При каждом перекрытии потока динамическое давление в нем внезапно падает до нуля, а статическое давление резко возрастает, перегоняя часть воды по вертикальной трубе в водонапорный бак. Это устройство используется для орошения земель, водоснабжения животноводческих ферм и т.д.
5. За счет разности давлений над и под крылом, создается подъемная сила самолета. При этом вокруг движущегося крыла возникает циркуляция воздуха, направленная по часовой стрелке. Над крылом скорости циркуляции и встречного воздушного потока складываются, под крылом – вычитаются. Поэтому относительная скорость движения воздуха над крылом превышает относительную скорость под крылом.
6. Аэрация почвы. Представим себе вспаханное поле, где валы чередуются с бороздами. Пусть ветер дует перпендикулярно к направлению борозд. Ясно, что наличие неровностей скажется на характере воздушного потока: вблизи земли линии тока будут искривлены и выровняются лишь на некоторой высоте над землей. Поэтому приземный слой воздуха является своеобразной трубкой тока переменного сечения, ограниченная снизу поверхностью земли, а сверху – ближайшей горизонтальной поверхностью, образованной невозмущенными линиями тока. Тогда в соответствии с уравнениями неразрывности и Бернулли давление воздуха над бороздами будет больше, чем над валами. Поэтому в поверхностном слое почвы возникает движение почвенного воздуха, направленное от оснований борозд к вершинам валов, что обеспечивает газообмен между почвой и атмосферой. Это явление и называется аэрацией почвы. Аэрация обогащает почвенный воздух кислородом, а приземный воздух – углекислотой, тем самым создавая благоприятные условия для развития растений.
6. Вязкость
Идеальная жидкость, т.е. жидкость без внутреннего трения – абстракция. Всем реальным жидкостям и газам в большей или меньшей степени присуще внутреннее трение, называемое также вязкостью.Вязкость проявляется, в частности, в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается. Примером может служить движение жидкости в стакане после того, как её перестают размешивать ложечкой.
Для выяснения закономерностей, которым обладают силы внутреннего трения, рассмотрим следующий опыт. В жидкость погружены две параллельные друг другу пластины (рис. 9.5), линейные размеры которых значительно превышают расстояние между ними. Нижняя пластина удерживается на месте, верхняя приводится в движение с некоторой скоростью  . Опыт показывает, что для перемещения верхней пластины с этой скоростью необходимо действовать на неё с некоторой определенной постоянной по модулю силой
. Опыт показывает, что для перемещения верхней пластины с этой скоростью необходимо действовать на неё с некоторой определенной постоянной по модулю силой  . Так как пластина не получает ускорения, то действие этой силы должно уравновешиваться равной ей по модулю противоположно направленной силой, которая и есть сила внутреннего трения, действующая на пластину при её движении в жидкости. Обозначим эту силу через
. Так как пластина не получает ускорения, то действие этой силы должно уравновешиваться равной ей по модулю противоположно направленной силой, которая и есть сила внутреннего трения, действующая на пластину при её движении в жидкости. Обозначим эту силу через  .
.
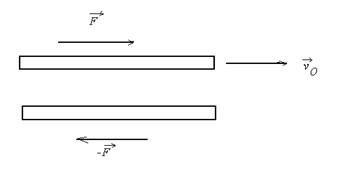
| Рис. 9.5. |
Опыт показывает, что
 , (9.10)
, (9.10)
где  – площадь пластин,
– площадь пластин,  – расстояние между ними,
– расстояние между ними, 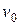 – скорость пластины, а
– скорость пластины, а  – коэффициент пропорциональности, зависящий от природы и состояния (например, от температуры) жидкости и называемый коэффициентом внутреннего тренияили простовязкостью жидкости (газа).
– коэффициент пропорциональности, зависящий от природы и состояния (например, от температуры) жидкости и называемый коэффициентом внутреннего тренияили простовязкостью жидкости (газа).
Нижняя пластина при движении верхней также подвергается действию силы  , равной по модулю
, равной по модулю 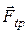 . Для того чтобы нижняя пластина оставалась неподвижной, силу
. Для того чтобы нижняя пластина оставалась неподвижной, силу  необходимо уравновесить с помощью силы
необходимо уравновесить с помощью силы 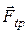 .
. 
Таким образом, при движении двух погруженных в жидкость пластин относительно друг друга между ними возникает взаимодействие, характеризуемое силой (9.10). Воздействие пластин друг на друга осуществляется через жидкость, заключенную между пластинами, передаваясь от одного слоя жидкости к другому. Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении z , перпендикулярном к пластинам, и по линейному закону
 (9.11)
(9.11)
Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорость, как и сами пластины. Согласно формуле (9.11)
 (9.12)
(9.12)
Тогда модуль силы внутреннего трения определится по формуле
 (9.13)
(9.13)
Величина 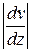 показывает, как быстро изменяется скорость в направлении оси z и представляет собой модуль градиента скорости.
показывает, как быстро изменяется скорость в направлении оси z и представляет собой модуль градиента скорости.
Единицей вязкости в СИ служит паскаль-секунда (Па·с). Это такая вязкость, при которой градиент скорости с модулем равным 1 м/с на 1 м приводит к возникновению силы внутреннего трения в 1 Н на 1 м2 поверхности касания слоев.
В СГС-системе единицей вязкости является пуаз (Пз), причем 1 Па·с = 10 Пз.
Коэффициент вязкости зависит от температуры. У жидкостей коэффициент вязкости уменьшается с повышением температуры. У газов, напротив, коэффициент вязкости с температурой растет.
7. Ламинарное и турбулентное течения
Наблюдаются два вида течения жидкости (или газа): ламинарное и турбулентное. Ламинарное течение – это течение, при котором жидкость как бы разделяется на слои, которые скользят относительно друг друга не перемешиваясь. Ламинарное течение стационарно.
При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется. Возникает энергичное перемешивание жидкости. Такое течение называется турбулентным.При этом течение нестационарно, так как скорость частиц изменяется беспорядочным образом. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места введения окрашенная жидкость равномерно распределяется по всему сечению потока.
Английский физик Рейнольдс установил, что характер течения зависит от значения безразмерной величины
 , (9.14)
, (9.14)
где ρ – плотность жидкости (или газа), v – средняя скорость потока (по сечению трубы), η – коэффициент вязкости жидкости, l – характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении и т.д.
Величина (9.14) называется числом Рейнольдса. При малых значениях числа Рейнольдса наблюдается ламинарное течение. Начиная с некоторого определенного значения  , называемого критическим, течение приобретает турбулентный характер. Практически критическое число Рейнольдса равно примерно 1000.
, называемого критическим, течение приобретает турбулентный характер. Практически критическое число Рейнольдса равно примерно 1000.
В число Рейнольдса входят две величины, зависящие от свойств жидкости: плотность и коэффициент вязкости. Отношение 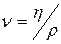 называется кинематической вязкостью. В отличие от неё величина
называется кинематической вязкостью. В отличие от неё величина  называется динамической вязкостью. Используя кинематическую вязкость, числу Рейнольдса можно придать следующий вид:
называется динамической вязкостью. Используя кинематическую вязкость, числу Рейнольдса можно придать следующий вид:  .
.
Число Рейнольдса служит важным параметром моделирования процессов, в частности при обтекании тел.
8. Течение вязкой жидкости в круглой трубе. Формула Пуазейля
Пусть по горизонтальной трубе радиуса 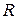 течет стационарный поток жидкости. Рассмотрим отрезок этой трубы длиной
течет стационарный поток жидкости. Рассмотрим отрезок этой трубы длиной  (рис. 9.6).
(рис. 9.6).

| Рис. 9.6. |
Частицы жидкости движутся вдоль трубы с разной скоростью: у самой стенки они прилипают к ней и имеют скорость равной нулю. По мере удаления от стенок скорость увеличивается и достигает максимального значения на оси трубы. Таким образом, величина скорости частиц жидкости является функцией  расстояния
расстояния  от оси трубы.
от оси трубы.
Для доказательства этого утверждения выделим воображаемый цилиндрический объем жидкости радиуса  . Жидкость, находящаяся внутри цилиндра, подвергается действию сил со стороны окружающей жидкости. Обозначим через
. Жидкость, находящаяся внутри цилиндра, подвергается действию сил со стороны окружающей жидкости. Обозначим через 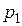 – давление жидкости у основания 1,
– давление жидкости у основания 1, 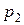 – давление жидкости у основания 2,
– давление жидкости у основания 2,  – площадь оснований. Так как движение частиц жидкости происходит вдоль трубы, рассмотрим силы, действующие лишь в этом направлении. На основание цилиндра действуют силы давления, величины которых
– площадь оснований. Так как движение частиц жидкости происходит вдоль трубы, рассмотрим силы, действующие лишь в этом направлении. На основание цилиндра действуют силы давления, величины которых 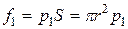 и
и  .
.
На боковую поверхность действует сила внутреннего трения 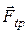 . Так как скорость жидкости внутри цилиндра больше, чем вне его, то сила
. Так как скорость жидкости внутри цилиндра больше, чем вне его, то сила 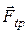 направлена в сторону, противоположную движению жидкости. Величина этой силы определяется по формуле
направлена в сторону, противоположную движению жидкости. Величина этой силы определяется по формуле  .
.
Здесь знак минус поставлен потому, что скорость убывает с расстоянием от оси трубы, следовательно, 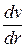 отрицательна и
отрицательна и 
При стационарном течении в трубе постоянного сечения скорости всех частиц жидкости остаются неизменными. Следовательно, должна быть равна нулю сумма проекций на направление оси трубы всех сил, действующих на цилиндр, т.е.  .
.
Здесь за положительное направление принято направление движения жидкости. Подставив сюда выражения для 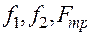 , найдем
, найдем 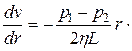
Разделив переменные, получим уравнение 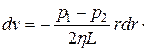
Интегрирование дает 
Постоянную интегрирования С можно найти из условия, что на стенке трубы, т.е. при 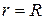 скорость частиц должна обращаться в нуль. Это дает
скорость частиц должна обращаться в нуль. Это дает 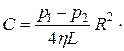
Окончательно имеем 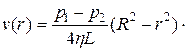
Отсюда видно, что при ламинарном течении скорость в зависимости от r меняется по параболическому закону и достигает максимума на оси трубы при 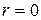 (как это и предполагалось ранее) (рис. 9.7).
(как это и предполагалось ранее) (рис. 9.7).
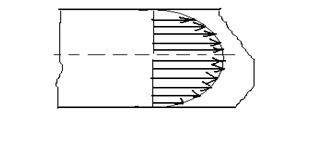
| Рис.9.7. Профиль скоростей при ламинарном течении жидкости в круглой трубе |
При турбулентном течении остается постоянной средняя скорость в каждой точке сечения трубы (рис.9.8). Вблизи стенок трубы скорость изменяется гораздо сильнее, чем при ламинарном течении, а в остальной части сечения скорость изменяется меньше.
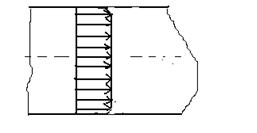
| Рис.9.8. Профиль скоростей при турбулентном течении жидкости в круглой трубе |
Полагая течение ламинарным, вычислим поток жидкости Q , т.е. количество жидкости m, протекающей через поперечное сечение трубы за единицу времени t: 
Разобьем поперечное сечение трубы на кольца ширины dr (рис. 9.9 ).
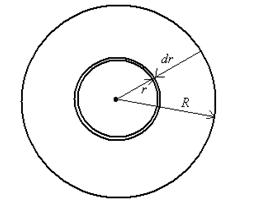
| Рис.9.9. |
Через кольцо радиуса r пройдет за секунду объем жидкости, равный произведению плотности жидкости 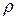 на площадь кольца
на площадь кольца  и на скорость течения в точках, находящихся на расстоянии r от оси трубы.
и на скорость течения в точках, находящихся на расстоянии r от оси трубы. 
Полный расход Q через все поперечное сечение трубы определяется суммой расходов через все кольцевые площадки, на которые может быть разбито поперечное сечение. Он равен интегралу от dQ в пределах от r=0 до r=R:

Эта формула называется формулой Пуазейля.
Из этой формулы следует, что поток жидкости сильно зависит от радиуса трубы. Кроме того, Q пропорционален отношению  , т.е. перепаду давления на единице длины трубы, а также обратно пропорционален вязкости жидкости
, т.е. перепаду давления на единице длины трубы, а также обратно пропорционален вязкости жидкости  .
.
Формула Пуазейля используется для экспериментального определения вязкости жидкостей и газов. Для этого жидкость или газ пропускают через трубку известного радиуса, измеряют перепад давления и поток Q . Затем на основании известных данных вычисляют  .
.
9. Движение тел в жидкостях и газах. Закон Стокса
При движении тела в жидкости или газе на него действуют две силы: сила  , направленная в сторону, противоположную движению тела, а вторая
, направленная в сторону, противоположную движению тела, а вторая  , перпендикулярная к этому направлению. Составляющие
, перпендикулярная к этому направлению. Составляющие  и
и  называются соответственно лобовым сопротивлением и подъемной силой.
называются соответственно лобовым сопротивлением и подъемной силой.
Ясно, что идеальная жидкость не оказывает движению тела никакого сопротивления.
Можно показать, что в несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления. Этот результат называется парадоксом Даламбера.
Учет вязкости жидкости существенно меняет картину взаимодействия тела с потоком. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности оказывается практически не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости, в котором имеется градиент скорости. Этот слой называется пограничным. В нем действуют силы трения, которые и приводят к возникновению лобового сопротивления.
Наличие пограничного слоя существенно меняет характер обтекания тела жидкостью. Полное обтекание тела становится невозможным. Действие сил трения в поверхностном слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри. Вихри уносятся потоком и постепенно затухают вследствие трения. При этом энергия вихрей расходуется на нагревание жидкости. Давление в образующейся за телом вихревой области оказывается пониженным. Поэтому результирующая сил давления будет отлична от нуля. Это давление в свою очередь обуславливает лобовое сопротивление.
Таким образом, лобовое сопротивление складывается из сопротивления трения и сопротивления давления.
При малых числах Рейнольдса сопротивление среды обусловлено практически только силами трения. Стокс установил, что сила сопротивления в этом случае пропорциональна коэффициенту динамической вязкости  , скорости
, скорости  движения тела относительно жидкости и характерному размеру тела
движения тела относительно жидкости и характерному размеру тела  :
:  ~
~ . Коэффициент пропорциональности зависит от формы тела. Чаще всего его определяют экспериментальным путем. Вычисления Стокса показали, что для шара коэффициент пропорциональности оказывается равным
. Коэффициент пропорциональности зависит от формы тела. Чаще всего его определяют экспериментальным путем. Вычисления Стокса показали, что для шара коэффициент пропорциональности оказывается равным  . Тогда сила лобового сопротивления для шара радиуса
. Тогда сила лобового сопротивления для шара радиуса  при
при  <<1 выражается формулой
<<1 выражается формулой  .
.
Эта формула известна под названием закона Стокса. Она может быть использована для нахождения вязкости.
При больших числах Рейнольдса влияние вязкости существенно лишь в тонком пограничном слое жидкости, прилегающем к поверхности тела. Как уже было отмечено, это влияние приводит к образованию вихрей сзади тела. Перед телом частицы жидкости в набегающем потоке практически останавливаются, движутся они только за телом. Поэтому, согласно уравнению Бернулли, создается разность давлений, действующих на переднюю  и заднюю р поверхности тела. Она равна
и заднюю р поверхности тела. Она равна 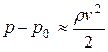 .
.
Таким образом, сила лобового сопротивления определяется силой сопротивления давления: 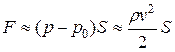 .
.
Для тел произвольной формы сила лобового сопротивления представляет вид 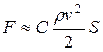 , где
, где  – наибольшая площадь поперечного сечения тела, С – коэффициент лобового сопротивления.
– наибольшая площадь поперечного сечения тела, С – коэффициент лобового сопротивления.
Величина С зависит от формы тела и числа Рейнольдса. Величина С уменьшается, если уменьшить площадь поперечного сечения тела в том месте, где происходит отрыв потока. Обтекаемые тела испытывают значительно меньшее сопротивление, чем тела с тупой задней частью, так как у первых отрыв потока происходит в задней узкой части тела.
10. Истечение жидкости из отверстия
Рассмотрим истечение идеальной несжимаемой жидкости из небольшого отверстия в широком открытом сосуде (рис. 9.10).

Рис. 9.10.
В жидкости мысленно выделим трубку тока, сечениями которой являются открытая поверхность жидкости  и сечение струи при выходе из отверстия
и сечение струи при выходе из отверстия  (если не принять специальных мер, то сечение струи будет меньше отверстия). Для всех точек каждого из этих сечений скорость жидкости
(если не принять специальных мер, то сечение струи будет меньше отверстия). Для всех точек каждого из этих сечений скорость жидкости  и высоту h над некоторым исходным уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления
и высоту h над некоторым исходным уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления  и
и 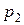 в обоих сечениях одинаковы и равны атмосферному. Скоростью
в обоих сечениях одинаковы и равны атмосферному. Скоростью  перемещения открытой поверхности жидкости ввиду ее малости можно пренебречь. Обозначим через v – скорость жидкости в сечении
перемещения открытой поверхности жидкости ввиду ее малости можно пренебречь. Обозначим через v – скорость жидкости в сечении (скорость истечения из отверстия). Поэтому уравнение Бернулли в данном случае упрощается следующим образом:
(скорость истечения из отверстия). Поэтому уравнение Бернулли в данном случае упрощается следующим образом: 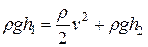 .
.
Сократив на плотность жидкости  , можно написать, что
, можно написать, что
 (9.15)
(9.15)
где  – высота открытой поверхности над отверстием.
– высота открытой поверхности над отверстием.
Формула (9.15) называется формулой Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, находящегося на глубине  под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты
под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты  (в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличатся от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода.
(в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличатся от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода.
Контрольные вопросы
1. Что такое давление в жидкости? Давление – величина векторная или скалярная? Какова единица измерения давления в СИ?
2. Сформулируйте и поясните законы Паскаля и Архимеда?
3. Что называют линией тока? трубкой тока?
4. Что характерно для установившегося течения жидкости?
5. Каков физический смысл и как вывести уравнение неразрывности для несжимаемой жидкости?
6. Какой закон выражает уравнение Бернулли для идеальной несжимаемой жидкости? Выведите это уравнение.
7. Что такое градиент скорости?
8. Каков физический смысл коэффициента динамической вязкости?
9. Какое течение называют ламинарным? Турбулентным? Что характеризует число Рейнольдса?
10. Поясните практическое применение методов Стокса и Пуазейля?
11. Каковы причины возникновения лобового сопротивления тела, движущегося в жидкости? Может ли оно быть равным нулю?
12. Как объяснить возникновение подъемной силы?
13. Найти выражение потенциальной энергии тела, погруженного в жидкость.
14. Найти зависимость выталкивающей силы Архимеда от глубины погружения.
15. Сосуд с жидкостью падает с ускорением  . Как меняется давление с изменением глубины?
. Как меняется давление с изменением глубины?
16. Может ли быть одинаковым давление в двух точках, лежащих на разных уровнях в установленной наклонно сужающейся трубке, по которой течет идеальная жидкость?
17. Почему струя жидкости, вытекающая из отверстия, по мере удаления от отверстия все больше сжимается?
Лекция №10. Движение в неинерциальных системах отсчета
1. Неинерциальные системы отсчета
Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона несправедливы. Эту несправедливость можно обнаружить на примере тела, покоящегося в некоторой инерциальной системе. В этом случае тело не испытывает действия сил  . Однако в неинерциальной системе, движущейся по отношению к инерциальным системам с ускорением, тело будет иметь ускорение а, отличное от нуля. Поскольку
. Однако в неинерциальной системе, движущейся по отношению к инерциальным системам с ускорением, тело будет иметь ускорение а, отличное от нуля. Поскольку  , равенство
, равенство 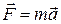 не соблюдается.
не соблюдается.
Рассмотрим две системы отсчета (рис.10.1), из которых система К является инерциальной, а система К' движется относительно К с некоторым ускорением и, следовательно, неинерциальна.
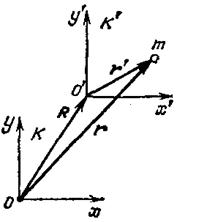
| Рис.10.1. |
Движение частицы относительно системы К характеризуется радиус-вектором  , а относительно системы К' – радиус-вектором
, а относительно системы К' – радиус-вектором 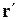 , а вектор
, а вектор  определяет положение начала координат системы К' относительно системы К.
определяет положение начала координат системы К' относительно системы К.
Эти радиус-векторы связаны соотношением 
Дифференцировав это соотношение дважды по времени, получим равенство
 (10.1)
(10.1)
Первая производная в (10.1) дает ускорение частицы а в системе К, вторая – ускорение  начала О' системы К' относительно системы К.
начала О' системы К' относительно системы К.
С производной 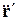 дело обстоит сложнее: если система К' в дополнение к поступательному движению еще и вращается с угловой скоростью
дело обстоит сложнее: если система К' в дополнение к поступательному движению еще и вращается с угловой скоростью  , то эта производная, кроме ускорения а' частицы в системе К', содержит слагаемые, в которые входят множителями либо
, то эта производная, кроме ускорения а' частицы в системе К', содержит слагаемые, в которые входят множителями либо  , либо
, либо  . Это обусловлено тем, что
. Это обусловлено тем, что 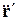 в (10.1) представляет собой производную, вычисленную наблюдателем, находящимся в системе К. А а' есть вторая производная
в (10.1) представляет собой производную, вычисленную наблюдателем, находящимся в системе К. А а' есть вторая производная 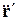 , вычисленная наблюдателем, который вращается вместе с системой К'. Вектор
, вычисленная наблюдателем, который вращается вместе с системой К'. Вектор 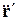 ведет себя в обеих системах по-разному.
ведет себя в обеих системах по-разному.
В случае, когда система К' движется относительно К поступательно (т.е.  ),
), 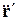 = а' и соотношение (10.1) можно представить в виде
= а' и соотношение (10.1) можно представить в виде
 (10.2)
(10.2)
2. Силы инерции
| -121 |
Умножим равенство (10.2) на массу частицы m: 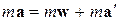 .
.
Здесь произведение 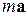 есть сила
есть сила 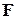 , с которой действуют на частицу другие тела согласно второму закону Ньютона. В результате получим уравнение
, с которой действуют на частицу другие тела согласно второму закону Ньютона. В результате получим уравнение
 (10.2)
(10.2)
Отсюда видно, что относительно системы К' частица ведет себя так, как если бы кроме «реальной» силы F на нее действовала дополнительная «фиктивная» сила 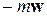 . Эта сила называется силой инерции. Обозначим ее как
. Эта сила называется силой инерции. Обозначим ее как . Фиктивность силы инерции надо понимать в том смысле, что не существует тел, воздействием которых была бы обусловлена эта сила. У нее нет «партнера», т.е. второй силы, предписываемой третьим законом Ньютона. Сила инерции обусловлена свойствами (неинерциальностью) той системы отсчета, в которой рассматриваются механические явления.
. Фиктивность силы инерции надо понимать в том смысле, что не существует тел, воздействием которых была бы обусловлена эта сила. У нее нет «партнера», т.е. второй силы, предписываемой третьим законом Ньютона. Сила инерции обусловлена свойствами (неинерциальностью) той системы отсчета, в которой рассматриваются механические явления.
Напишем уравнение (10.2) следующим образом:
 (10.3)
(10.3)
Это уравнение справедливо в неинерциальной системе отсчета. По форме оно аналогично уравнению второго закона Ньютона. Следовательно, введение сил инерции позволяет описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения. В этом заключается смысл введения сил инерции.
Каждый, кто пользуется городским транспортом, испытывал на себе действие сил инерции. Так, при резком торможении автобуса или трамвая пассажиры испытывают силу, толкающую их вперед; стоящие вблизи стекла, ограждающего кабину водителя, могут при этом под действием «фиктивной» силы инерции набить себе вполне реальную шишку.
Введение сил инерции не является совершенно необходимым. Любое движение можно рассмотреть по отношению к инерциальной (например, гелиоцентрической) системе отсчета. Однако на практике часто представляет интерес именно движение тел по отношению к неинерциальным системам отсчета (например, по отношению к Земле). Использование сил инерции позволяет решить соответствующую задачу непосредственно в такой системе отсчета, что часто бывает намного проще, чем решение в инерциальной системе.
Характерной особенностью сил инерции является их пропорциональность массе тела. В этом отношении силы инерции сходны с гравитационными силами. Представим себе, что мы находимся в закрытой кабине, а кабина движется вверх относительно инерциальных систем с постоянным ускорением 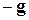 в направлении. Тогда всякое тело внутри кабины будет вести себя так, как если бы на него действовала сила инерции
в направлении. Тогда всякое тело внутри кабины будет вести себя так, как если бы на него действовала сила инерции 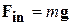 . В частности, пружина, к концу которой подвешено тело массой m, растянется так, чтобы упругая сила уравновесила силу инерции. Однако такие же явления наблюдались бы и в том случае, если бы кабина была неподвижной, а под ней находилась Земля. Не имея возможности «выглянуть» из кабины, никакими опытами, проводимыми внутри кабины, мы не могли бы определить, чем обусловлена сила
. В частности, пружина, к концу которой подвешено тело массой m, растянется так, чтобы упругая сила уравновесила силу инерции. Однако такие же явления наблюдались бы и в том случае, если бы кабина была неподвижной, а под ней находилась Земля. Не имея возможности «выглянуть» из кабины, никакими опытами, проводимыми внутри кабины, мы не могли бы определить, чем обусловлена сила  – ускоренным движением кабины или действием гравитационного поля Земли. Основываясь на это утверждение, говорят об эквивалентности сил инерции и сил тяготения. Эта эквивалентность Эйнштейном была положена в основу общей теории относительности.
– ускоренным движением кабины или действием гравитационного поля Земли. Основываясь на это утверждение, говорят об эквивалентности сил инерции и сил тяготения. Эта эквивалентность Эйнштейном была положена в основу общей теории относительности.
3. Силы инерции при ускоренном поступательном движении
системы отсчета
Пусть на потолке вагона на нити висит шарик массой m. Пока вагон покоится и движется равномерно и прямолинейно, нить, удерживающая шарик, занимает вертикальное положение. При этом сила тяжести  уравновешивается реакцией нити
уравновешивается реакцией нити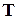 .
.
Если вагон поезда набирает скорость, то нить отклонится от вертикали назад (рис. 10.3).
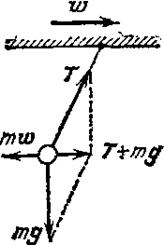
| Рис.10.3 |
Обозначим ускорение поезда  . Относительно Земли (которую мы считаем инерциальной системой отсчета) шарик имеет такое же ускорение
. Относительно Земли (которую мы считаем инерциальной системой отсчета) шарик имеет такое же ускорение  ,как и вагон. Это ускорение сообщается шарику силой
,как и вагон. Это ускорение сообщается шарику силой  . Она равна сумме силы натяжения нити Т и силы тяжести
. Она равна сумме силы натяжения нити Т и силы тяжести  , т.е.
, т.е. 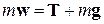 . Относительно системы отсчета, связанной с ускоренно движущимся вагоном, шарик покоится. Отсутствие ускорения шарика относительно вагона можно объяснить тем, что сила
. Относительно системы отсчета, связанной с ускоренно движущимся вагоном, шарик покоится. Отсутствие ускорения шарика относительно вагона можно объяснить тем, что сила 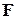 уравновешивается силой инерции, равной (
уравновешивается силой инерции, равной (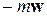 ), так как на шарик никакие друге силы не действуют.
), так как на шарик никакие друге силы не действуют.
Проявление сил инерции при поступательном движении наблюдается в повседневных явлениях. Например, когда поезд набирает скорость, пассажир, сидящий по ходу поезда, под действием силы инерции прижимается к спинке сиденья. Наоборот, при торможении поезда сила инерции направлена в противоположную сторону, и пассажир отделяется от спинки сиденья. Силы инерции особенно заметны при внезапных торможениях поезда. Они проявляются в перегрузках, которые возникают при запуске и торможении космических кораблей.
4. Силы инерции при равномерном вращательном
движении системы отсчета. Центробежная сила инерции
Рассмотрим поведение тел в системе отсчета К', вращающейся относительно инерциальной системы К с постоянной угловой скоростью  : в системе отчета К' поступательная составляющая движения отсутствует. Ясно, что она неинерциальна. Примером рассматриваемого движения может служить система, связанная с вращающимся диском электропроигрывателя.
: в системе отчета К' поступательная составляющая движения отсутствует. Ясно, что она неинерциальна. Примером рассматриваемого движения может служить система, связанная с вращающимся диском электропроигрывателя.
Укрепим на диске радиально направленный стержень, на который наденем шарик, «привязанный» к оси диска пружиной (рис. 10.4).
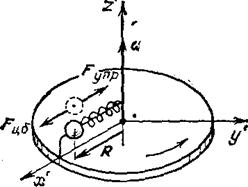
| Рис. 10.4. Шарик может перемещаться только вдоль радиуса диска, скользя без трения по тонкому стержню |
Пока диск не вращается, пружина не деформирована. При раскручивании диска шарик растягивает пружину до тех пор, пока упругая сила  не станет равной произведению массы шарика на его ускорение. Обозначим через
не станет равной произведению массы шарика на его ускорение. Обозначим через  – радиус – вектор, проведенный к шарику от центра диска и перпендикулярно к оси вращения. Его модуль дает расстояние R шарика от оси вращения системы К'. Так как шарик движется от центра и вдоль радиуса окружности вместе с равномерно вращающимся диском, ускорение шарика равно по модулю центростремительному ускорению и направлено противоположно ему:
– радиус – вектор, проведенный к шарику от центра диска и перпендикулярно к оси вращения. Его модуль дает расстояние R шарика от оси вращения системы К'. Так как шарик движется от центра и вдоль радиуса окружности вместе с равномерно вращающимся диском, ускорение шарика равно по модулю центростремительному ускорению и направлено противоположно ему:
 (10.4)
(10.4)
Таким образом, при вращении диска
 (10.5)
(10.5)
Относительно системы отсчета К', связанной с диском, шарик покоится. Формально это можно объяснить тем, что в данной системе кроме силы  на шарик действует сила инерции
на шарик действует сила инерции
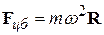 , (10.6)
, (10.6)
направленная вдоль радиуса от оси вращения диска.
Определяемая выражением (10.6) сила  называется центробежной си
называется центробежной си
– Конец работы –
Эта тема принадлежит разделу:
Уфа 2008
РОССИЙСКОЙ ФЕДЕРАЦИИ... ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ... ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Потенциальная энергия упруго деформированного стержня равна
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов