рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Уфа 2008
Реферат Курсовая Конспект
Уфа 2008
Уфа 2008 - раздел Образование, Министерство Образования И Науки ...
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ им. М. Акмуллы
М. А. ФАТЫХОВ
МЕХАНИКА
Учебное пособие
Уфа 2008
ББК 22.2я73 Ф 27Цели и задачи изучения дисциплины
– формирование современной естественнонаучной картины мира; – понимание роли этого раздела физики в построении физической картины мира;Требования к уровню подготовки
– иметь представление о теориях фундаментальных механических явлений как о целостной системе знаний о природе, понимать их модельный характер и… – знать основные понятия и законы в рамках изучаемого курса; – иметь представление о месте изучаемого курса в общем курсе физики;Место дисциплины в учебном процессе и виды учебной работы
Дисциплина общей трудоемкостью 360 часов рассчитан на один семестр (I семестр). Лекции 3 часа в неделю, практические занятия 3 часа в неделю, лабораторный практикум – 4 часа в неделю. Вычислительный эксперимент проводится во время лабораторного практикума.
Распределение учебных часов
Учебно-тематический план
Содержание курса
Введение.Предмет и задачи физики. Методы физических исследований. Сочетание экспериментальных и теоретических методов в познании окружающей среды. Модельный характер физических законов. Физические величины, их измерение и оценка точности и достоверности полученных результатов. Системы единиц физических величин. Связь физики с другими естественными науками.
Механика.Введение. Предмет и задачи классической механики. Механическое движение. Пространство и время. Система координат. Системы отсчета. Эталоны времени и длины. Модели механики: материальная точка, система материальных точек, твердое тело, сплошная среда.
Кинематика материальной точки.Задачи кинематики, кинематическиехарактеристики движения: радиус-вектор, перемещение, скорость, ускорение, тангенциальное и нормальное ускорения. Траектория движения и пройденный путь. Уравнения движения. Поступательное и вращательное движения материальной точки. Составное движение материальной точки. Относительность движения. Закон сложения скоростей. Принцип независимости движений. Преобразования Галилея для координат и скоростей.
Перемещение и путь при равномерном и равноускоренном прямолинейном движении. Движение точки по окружности. Угловое перемещение, угловая скорость, угловое ускорение. Связь линейных и угловых величин. Векторы угловой скорости и углового ускорения.
Колебательное движение. Гармонические колебания, их характеристики: амплитуда, частота и фаза колебаний. Кинематические уравнения гармонических колебаний. Смещение, скорость и ускорение при гармоническом колебательном движении. Описание гармонических колебаний одного направления с одинаковыми и разными частотами. Биения. Понятие о спектрах и гармоническом (спектральном) анализе. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
Динамика материальной точки.Первый закон Ньютона. Инерциальные системы отсчета. Взаимодействие тел. Понятие о силе и ее измерения. Принцип независимости действия сил. Силы в природе. Второй закон Ньютона. Масса и ее измерение, аддитивность массы. Инертная масса. Импульс. Сила как производная импульса по времени. Силы трения. Жидкое трение. Трения покоя и скольжения. Роль силы трения покоя при качении тел. Трение качения. Значение силы трения в природе и технике. Принцип суперпозиции. Принцип относительности Галилея. Третий закон Ньютона. Применение законов ньютоновской динамики в решении простейших задач: движение при наличии силы тяжести. Вес и невесомость.
Динамика системы материальных точек. Законы сохранения.Системы материальных точек. Силы внешние и внутренние. Движение системы материальных точек. Центр масс. Координаты центра масс. Движение центра масс. Замкнутые системы. Закон сохранения импульса замкнутой системы материальных точек. Постоянство скорости центра масс замкнутой системы. Примеры проявления закона сохранения импульса: сохранения плоскости качаний маятника, реактивное движение. Уравнения Мещерского и Циолковского.Задача двух тел. Приведенная масса. Движение в гравитационном поле.
Работа силы, мощность. Консервативные и неконсервативные силы и системы. Независимость работы консервативной силы от траектории. Потенциальная энергия. Связь силы с потенциальной энергией. Кинетическая энергия. Закон сохранения энергии в неконсервативной системе. Применение законов сохранения импульса и энергии к анализу упругого и неупругого соударений.
Момент импульса материальной точки относительно произвольного центра. Момент силы. Сохранение момента импульса материальной точки при движении под действием центральной силы. Момент импульса системы материальных точек, закон сохранения импульса замкнутой системы. Законы сохранения и принципы симметрии пространства и времени.
Роль законов сохранения в физике.
Механика твердого тела.Твердое тело как система материальных точек. Абсолютно твердое тело. Плоское движение твердого тела. Поступательное и вращательное движение абсолютно твердого тела. Мгновенные оси вращения. Понятие о степенях свободы и связях. Вращение относительно неподвижной оси. Пара сил. Момент пары. Момент инерции и момент импульса твердого тела. Второй закон Ньютона для вращающегося твердого тела. Теорема Штейнера. Закон сохранения момента импульса твердого тела, примеры его проявления.
Вращение твердого тела вокруг неподвижной точки и оси. Кинетическая энергия вращающегося тела. Кинетическая энергия тела при плоском движении. Свободные оси вращения. Гироскоп.
Условия равновесия твердого тела. Виды равновесия. Центр тяжести.
Механика жидкостей и газов.Механические свойства жидкостей и газов. Давление в жидкостях и газах. Измерение давления. Манометры. Распределение давления в покоящихся жидкостях и газах. Сила Архимеда. Условие плавания тел.
Описание движения жидкостей. Стационарное слоистое движение жидкости. Уравнение неразрывности струи. Уравнение Бернулли для идеальной жидкости и ее следствия. Течение жидкости в трубах. Движение тел в жидкостях и газах. Формула Стокса. Вязкость. Закон Кулона-Амонтона. Формула Пуазейля. Истечение жидкости из отверстия. Формула Торричелли. Ламинарное и турбулентное течения. Число Рейнольдса.
Силы, действующие на тело, движущееся в жидкости: сила лобового сопротивления и подъемная сила. Подъемная сила крыла самолета.
Механика деформируемых твердых тел. Упругие свойства твердых тел. Виды упругих деформаций. Упругие силы. Закон Гука для различных деформаций: одновременное растяжение (сжатие), всестороннее сжатие, сдвиг, кручение. Модули упругости, упругое последействие и упругий гистерезис.
Потенциальная энергия упруго деформированного тела. Плотность энергии.
Движение в неинерциальных системах отсчета (НИСО).Неинерциальные системы отсчета. Описание движения в неинерциальных системах отсчета. Силы инерции. Сила инерции в прямолинейно движущейся НИСО. Равномерно вращающаяся НИСО. Центробежная сила инерции. Сила Кориолиса. Проявление сил инерции на Земле: зависимость веса тела от широты места, маятник Фуко.
Механика колебаний и волн.Движение под действием упругих и квазиупругих сил. Уравнение движения простейших механических колебательных систем без трения: пружинный, математический, физический и крутильный маятники. Собственная частота колебаний. Кинетическая, потенциальная и полная энергия колеблющегося тела.
Уравнение движения колебательных систем с трением. Затухающие колебания. Коэффиицент затухания, логарифмический декремент, добротность, их связь с параметрами колебательной системы.
Вынужденные колебания. Энергетические соотношения при вынужденных колебаниях. Резонанс. Вынужденные колебания при наличии трения.
Нелинейные колебательные системы. Анализ уравнений движения ангармонического и параметрического осцилляторов. Параметрический резонанс. Автоколебания. Роль механических колебаний в технике.
Механические колебания в связанных системах. Распространение колебаний в однородной упругой среде. Продольные и поперечные волны. Скорость распространения волны. Волновой фронт. Плоские, цилиндрические и сферические волны. Уравнение плоской гармонической бегущей волны. Мгновенное распределение смещений, скоростей и деформаций в бегущей волне. Энергия бегущей волны. Поток энергии. Вектор Умова. Интенсивность волны. Интерференция волн. Отражение волн. Стоячие волны. Мгновенное распределение относительных смещений и скоростей в стоячей волне. Энергетические соотношения в стоячей волне. Суперпозиция колебаний. Понятие о спектральном анализе. Его физический смысл.
Природа звука. Скорость звука в твердых телах, жидкостях и газах. Измерение скорости звука. Акустическое давление и скорость частиц в звуковой волне. Интенсивность звука. Источники и приемники звука. Звуковые волны в струнах и трубах. Колебания мембраны (телефон, микрофон, громкоговоритель). Акустический резонанс. Голосовой и слуховой аппарат человека. Запись и воспроизведение звука. Объективные и субъективные характеристики звука. Анализ и синтез звуков.
Понятие об инфразвуке. Ультразвук и его применение.
Всемирное тяготение.Движение планет. Законы Кеплера. Закон тяготения Ньютона, постоянная тяготения и ее измерение. Гравитационная масса.
Понятие о поле тяготения. Вещество и поле как виды материи. Напряженность и потенциал поля тяготения. Однородное и центральное поле. Применение закона сохранения энергии Ки движению в центральном гравитационном поле. Космические скорости. Достижения в области освоения и исследования космического пространства.
Эйнштейновский принцип эквивалентности сил инерции и сил тяготения.
Элементы специальной теории относительности (СТО).Представления Ньютона о свойствах пространства и времени. Инвариантность второго закона Ньютона относительно преобразований Галилея. Границы применимости механики Ньютона. Постулаты Эйнштейна
Относительность одновременности в СТО. Преобразования Лоренца. Следствия из преобразований Лоренца. Интервал между событиями. Преобразование и сложение скоростей. Релятивистский импульс. Релятивистская форма закона Ньютона. Релятивистское выражение для энергии. Взаимосвязь массы и энергии покоя. Частицы с нулевой массой. Законы сохранения массы, энергии и импульса в СТО, их проявления.
Примерная тематика семинарских занятий
1. Кинематика прямолинейного движения.
2. Кинематика криволинейного движения и вращение тела вокруг неподвижной оси.
3. Динамика материальной точки и тела, движущегося поступательно.
4. Динамика криволинейного движения материальной точки.
5. Динамика вращательного движения твердого тела.
6. Статика. Упругие деформации твердого тела.
7. Гравитационное взаимодействие. Движение тел в поле тяготения.
8. Работа и энергия. Потенциальная энергия упруго деформированного тела.
9. Законы сохранения в механике. Закон сохранения импульса, энергии и момента импульса.
10. Механические колебания.
11. Волны в упругой среде.
12. Механика жидкостей и газов.
13. Релятивистская механика.
Вычислительный эксперимент
2. Вес и невесомость. 3. Движение по наклонной плоскости. 4. Реактивное движение.Средства обеспечения дисциплины
В качестве средств обеспечения дисциплины предполагается использование лаборатории механики, лаборатории лекционных демонстраций и класс вычислительной физики с программным обеспечением.
Рекомендуемая литература
Основная литература:
1. Сивухин Д.В. Курс общей физики. Т.1. Механика. – М.: Наука, 1979.
2. Лаврова И.В. Курс физики. – М.: Просвещение, 1981.
3. Грабовский Р.И. Курс физики. – М.: Высшая школа, 1980.
4. Архангельский М.М. Курс физики. Механика. – М.: Просвещение, 1975.
5. Александров Н.В., Яшкин А.Я. Курс общей физики. Механика. – М.: Просвещение, 1978.
6. Савельев И.В. Курс общей физики. Т.1. – М.: Высшая школа, 1989; или Кн.1. – М.: Высшая школа, 1998.
Задачники:
1. Волькенштейн В.С. Сборник задач по общему курсу. – М.: Наука, 1979 (другие годы издания).
2. Иродов И.Е.Задачник по общей физике. – М.: Наука, 1988.
3. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Высшая школа, 1988.
Дополнительная литература:
1. Гулд Х., Тобочник Я. Компьютерное моделирование в физике. Т.1-2. – М.: Мир, 1990.
2. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989.
3. Хайкин С.Э. Физические основы механики. – М.: Наука, 1979.
4. Матвеев А.Н. Механика и теория относительности. – М.: Высшая школа, 1986.
5. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Курс общей физики. Механика. – М.: Академия, 2001.
Лекция №1. Введение
1. Предмет физики, её связь с другими естественными науками
Физика – наука, изучающая наиболее общие свойства материи и формы её движения. Под материей подразумевается весь окружающий нас мир, включающий два известных нам вида материи – вещество (в твердом, жидком, газообразном состоянии и плазме) и поле (гравитационное, электромагнитное, поле ядерных сил), которые способны видоизменяться и превращаться друг в друга и описываются законами физики.
Неотъемлемым всеобщим свойством материи является движение, понимаемое в самом широком смысле, т.е. не только как механическое перемещение тел в пространстве, но и как изменение и развитие как таковое. Известны следующие виды физических форм движения: механические, атомно-молекулярные, гравитационные, электромагнитные, внутриатомные и внутриядерные процессы. Они являются общими потому, что содержатся во всех более сложных формах движения материи, изучаемых другими науками. Например, процессы жизнедеятельности организмов, изучаемых биологией, всегда сопровождаются механическими, электрическими, внутриатомными и другими физическими процессами. Таким образом, предмет исследований физики составляют общие закономерности явлений природы.
Физика – одна из основных общих естественных наук, в которых изучаются законы неживой природы. Связь физики с другими естественными науками выражается прежде всего в том, что, выявляя общие закономерности явлений природы, её макро- и микромира, физика фундаментальна по отношению к ним. Физика позволяет создавать приборы и вырабатывать методы исследования, необходимые для развития других наук. Например, в развитии биологии большое значение имели микроскоп, в астрономии – телескоп, в химии – спектральный анализ и др. Все естественные науки широко и плодотворно применяют метод меченых атомов, электронную аппаратуру и другие физические приборы, а также различные методы физических исследований. Справедлива, конечно, и обратная связь: развитие других естественных наук ставит перед физикой новые задачи и способствует её прогрессу и совершенствованию. Только на стыке физики и биологии возникли ряд новых смежных научных направлений, таких как биофизика, биомеханика – наука, изучающая законы движения биологических систем, биоэнергетика – наука, занимающаяся вопросами механизма генерации и переноса энергии в живых объектах, радиобиология – наука, изучающая действие внешних физических полей и излучений на живые организмы, современная генетика, рассматривающая явления наследственности на молекулярном уровне. В последние годы особенно пристальное внимание уделяется изучению биоэлектрических явлений, обусловливающих возникновение биоэлектрических потенциалов, а также агрофизике – науке о влиянии водовоздушных, тепловых и световых режимов на развитие растений и животных и возможности их регулирования и создания фитотронов (станций искусственного климата). Возникли другие смежные науки, такие как астрофизика, физическая химия, электрофизика и др.
Развитие математики и физики также очень тесно связано друг с другом. Без знания математики нельзя изучать физику, так как все закономерности в физике выражаются посредством чисел. Только с помощью математического аппарата можно разобраться и проанализировать сложные закономерности, которые имеют место в физических явлениях. Разработка математических методов всегда преследует, в том или ином виде, цель практическую – дать средство анализа закономерностей природы. Поэтому изучение физики тесно связано с изучением математики даже в той части физики, которую называют общей и экспериментальной, так как здесь исследователь определяет количественные изменения различных величин.
2. Методы физических исследований
Методом физических исследований является материалистическая диалектика, рассматривающая все явления окружающего нас мира в их взаимосвязи и взаимодействии, в их развитии и изменении. Поэтому рассматриваемые ниже методы физических исследований применимы и в других естественных науках.
Всякое физическое исследование начинается с наблюдения, т.е. с изучения физических явлений в естественной, природной обстановке. Затем на основании размышлений и логических обобщений высказывается рабочая гипотеза – научное предположение, объясняющее эти явления. Гипотеза проверяется экспериментом, т.е. изучением явлений путем их воспроизведения в искусственных, лабораторных условиях. Гипотеза, подтвержденная экспериментом, становится научной теорией. Физическая теория представляет собой систему основных идей, обобщающих опытные данные и отражающих объективные закономерности природы. Физическая теория дает объяснение целой области явлений природы с единой точки зрения. Теория в дальнейшем подвергается неоднократной проверке практикой, которая вносит в теорию многочисленные дополнения и уточнения.
В связи с изложенным целесообразно сделать одно замечание о связи теории и эксперимента в физике. Теория играет исключительно важную роль. Без нее современная физика немыслима. Однако необходимо правильно представлять себе истинную роль теории в физике. Чистая теория в основном основывается на математике, а математика имеет дело с абстрактными объектами и понятиями, подчиняющимися определенной системе аксиом. Единственное требование, предъявляемое в чистой математике к ее понятиям и аксиомам, сводится к их логической непротиворечивости. Все свои результаты чистая математика получает из этих аксиом путем логических рассуждений, основанных на правилах формальной логики. Содержание этих результатов, очевидно, не может выйти за пределы логических связей между различными объектами и понятиями чистой математики. В этом смысле чистая математика является логически замкнутой дисциплиной. Такая замкнутость и логическая согласованность придают чистой математике, а, следовательно, и теории эстетическую привлекательность и доставляют чувство глубокого удовлетворения всякому уму.
Однако нужно заметить, что строго замкнутая сама в себе теория оторвана от реальной действительности и не может быть использована в других науках и практической деятельности человека. Чтобы теория стала мощным средством при физических исследованиях, необходимо установить связи между абстрактными математическими объектами и понятиями – с одной стороны – и реальными объектами и явлениями природы – с другой. Математические понятия и объекты должны появляться не как чисто логические категории, а как абстракции каких-то реальных объектов или процессов природы. Так, точка является абстракцией физического тела достаточно малых размеров, прямая линия – абстракцией достаточно тонкого твердого стержня или светового пучка в однородной среде. Вопрос о справедливости математики сводится к справедливости ее аксиом. Справедливость же самих аксиом может быть установлена опытным и только опытным путем.
Правда, опыт с математическими объектами нельзя осуществить в чистом виде, поскольку эти объекты являются идеализациями и не встречаются в природе. Всякий опыт выполняется с реальными телами. Математическую строгость надо понимать в смысле логической согласованности ее выводов, но не в смысле обоснования математических аксиом.
Одной математической строгости недостаточно для физики, как и для всякой другой опытной науки, имеющей дело с реальными объектами и явлениями природы. Всякое теоретическое исследование, выполненное математически строго, никогда не может считаться и физически строгим. Во-первых, такие исследования всегда основываются на определенных законах, справедливость которых в конце концов доказывается опытным путем, а опыты и физические измерения неизбежно сопровождаются ошибками, т.е. выполняются с определенной точностью. Вне пределов этой точности физический закон может оказаться не верным. Во-вторых, всякий реальный физический объект характеризуется бесконечным разнообразием свойств. Учесть все эти свойства невозможно не только потому, что большинство из них нам просто неизвестно, но и потому, что это практически не осуществимо. При построении теории физика заменяет реальные объекты их идеализированными моделями, приблизительно правильно передающими не все свойства реальных объектов, а только те из них, которые существенны в рассматриваемом круге вопросов. Какие свойства реальных объектов существенны, а какие не играют заметной роли – на этот вопрос в конце концов может ответить только опыт, которому принадлежит решающее слово в вопросе о правильности всякой физической теории и пределах ее применимости. Если физический закон применен вне области, где он справедлив, а идеализированная модель правильно передает не все свойства реальных объектов, существенные для рассматриваемого круга явлений, то возникающие вследствие этого пороки теории, понятно, не могут быть исправлены никакой строгостью математических рассуждений и расчетов.
Последнее замечание имеет и практическую ценность. Конечно, после того как идеализированная модель построена, не будет ошибкой производить все дальнейшие расчеты математически абсолютно точно, хотя при этом и использовались физические законы, верные только приближенно. Однако сплошь и рядом такие расчеты очень громоздки и даже практически не осуществимы из-за их сложности. Между тем точность уже обесценена ошибками физических законов и несовершенствами идеализированной модели, положенной в основу расчета. Поэтому можно и нужно перейти к приближенным расчетам. Такие расчеты столь же хороши, что и «точные», если их ошибки не превосходят ошибок, обусловленных неточностью применяемых физических законов и несовершенствами идеализированных моделей.
3. Роль модельных представлений в физике
Моделирование – один из основных методов познания, который заключается в построении моделей реально существующих объектов, замене реального объекта его подходящей моделью и последующего исследования построенной модели.
Под моделью(от латинского слова modulus – мера, образец) объекта или явления в физике мы будем понимать некий другой объект, реализованный в рамках той или иной знаковой системы. Этот объект:
- сопоставляется реально существующему природному объекту;
- подобен исходному объекту, т.е. адекватно отражает свойства исходного объекта;
- строится с определенной целью, заранее определяемой субъектом моделирования;
- отражает лишь некоторые свойства исходного объекта, признанные субъектом моделирования существенными;
- создается для получения информации об исходном объекте, необходимой для решения определенной задачи.
Для одного физического явления может быть несколько моделей или даже несколько семейств моделей. В таком случае эти модели должны взаимно однозначно соответствовать (изоморфизм моделей) или частично односторонне соответствовать одна модель другой (гомоморфизм).
В науке, где опыт является первичным источником знания, роль моделей важна, так как без модели нет теории. Для получения знания недостаточно проведения опытов, нужно также изучить теорию, уметь работать с моделями. Компьютерный эксперимент имеет дело именно с моделями физических процессов. Основное применение компьютерного эксперимента в образовании – демонстрации и лабораторные работы. Компьютерная лабораторная работа представляет собой вычислительный эксперимент, требующий активной деятельности студента. Такая работа не может в полной мере познакомить студентов с реальными приборами, но остальные функции лабораторной работы она выполняет. Компьютерная модель обладает также демонстрационной наглядностью, позволяет студентам «увидеть невидимое» – образование интерференционной картины с летящими фотонами, релаксацию кристаллической решетки вблизи дефектов и многое другое, чего не увидишь в реальном эксперименте.
Компьютерные лабораторные работы создаются там, где нужно проникнуть в строение вещества, проанализировать важные модели там, где условия экстремальны и т.п.
Компьютерный эксперимент представляет собой новую методику изучения физики, сохраняя при этом большинство дидактических черт реального эксперимента. Он расширяет круг опытов, проводимых студентами, не сужает применение обычного эксперимента, а дополняет его.
Компьютерный эксперимент, как и натурный, обеспечивает фундаментальную базовую подготовку по курсу общей физики.
Модельные демонстрации, модельные лабораторные работы, модельные конструкторы – это динамические иллюстрации, входящие в интерактивные модели. Все классы моделей могут отображать внешний вид и поведение системы, числовую информацию о ней, графики, иллюстрирующие взаимосвязи величин, а также визуализировать глубинные, скрытые в реальном мире от глаз и приборов процессы и даже не существующие в реальности объекты и понятия. Отличие различных классов моделей состоит в мере предоставляемой свободы управления и модернизации модели.
Простейшей моделью тел, движение которых изучает классическая механика, является материальная точка Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.Материальных точек в природе не существует. Материальная точка есть абстракция, идеализированный образ реально существующих тел. Можно или нельзя то или иное тело при изучении какого-либо движения принять за материальную точку – это зависит не столько от самого тела, сколько от характера движения, а также от содержания вопросов, на которые мы хотим получить ответ. Абсолютные размеры тела при этом не играют роли. Важны относительные размеры, т.е. отношения размеров тела к некоторым расстояниям, характерным для рассматриваемого движения. Например, при вычислении траектории, по которой Земля движется вокруг Солнца, Землю можно рассматривать как материальную точку. Поэтому достаточно рассмотреть движение только одной точки, например центра Земли, и считать, что все вещество Земли как бы сосредоточено в этой геометрической точке. Такая идеализация сильно упрощает задачу об орбитальном движении Земли, сохраняя, однако, все существенные черты этого движения. При рассмотрении же движения тел по поверхности Земли она уже не является материальной точкой. Кроме того, сравнивать можно не только линейные размеры тел, но и другие физические величины (например, давление, скорость, период и т.д.).
Любое тело, размерами которого пренебречь нельзя, можно считать как совокупность материальных точек.
Под воздействием тел друг на друга тела могут деформироваться, т.е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель – абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между точками (или точнее между двумя частицами) этого тела остается постоянным.
Понятия материальной точки, абсолютно твердого тела, идеальной жидкости и идеального газа и др. – абстрактные, но их введение позволяет наглядно и проще исследовать свойства соответствующих тел и облегчает решение практических задач.
4. Физические величины, их измерение и оценка точности
и достоверности полученных результатов
Физика принадлежит к классу точных наук, где количественное определение происходящих изменений играет важную роль. В физических исследованиях определяются изменения различных физических величин, таких, например, как скорость, длина, сила и т.д. Физические величины – это свойства тела или характеристики процесса, изменения которых можно определить количественно посредством измерений, т.е. посредством сравнения данной величины с определенной величиной того же рода, принятой за единицу.
Точное и правильное измерение физических величин во время наблюдений и опытов составляет существенную часть всякого научного исследования в физике.
Под точностьюизмерений понимается их качество, отражающее близость результатов к измеряемой величине.
Если общая относительная погрешность измерений, включающая и систематическую, и случайную составляющие У, то количественно точность принимается равной 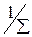 . Точность, как и относительная погрешность – величина безразмерная.
. Точность, как и относительная погрешность – величина безразмерная.
Часто стараются произвести измерения с наибольшей достижимой точностью, т.е. сделать погрешность по возможности малой. Однако следует иметь в виду, что чем точнее мы хотим измерить какую-либо величину, тем труднее это сделать. Поэтому не следует требовать от измерений большей точности, чем это необходимо для решения поставленной задачи. Для изготовления книжной полки длину досок вполне достаточно измерять не точнее, чем до 0,5 – 1 см, т.е. с погрешностью около 1 %, для производства некоторых деталей шарикоподшипников допустима погрешность не более 0,001 мм, или около 0,01 %, а при измерении длин волн спектральных линий иногда величина погрешности не должна превышать 10-11 см, или около 10-5 %.
Очень часто повышение точности измерений позволяет выявить новые закономерности. Действительно, всякий закон, устанавливающий количественную связь между физическими величинами, выводится в результате опыта, основой которого служат измерения. Он может считаться верным лишь с той степенью точности, с какой выполнены измерения, положенные в его основу. Так, например, существует закон сохранения вещества, по которому сумма масс веществ, вступающих в химическую реакцию, равна массе продуктов реакции. Однако при химической реакции поглощается или выделяется энергия. Поэтому в соответствии с теорией относительности масса продуктов реакции несколько отличается от суммы реагирующих масс. При сгорании угля это различие составляет 1 г на 3000 т угля. Чтобы это заметить, нужно произвести взвешивание с относительной погрешностью не более 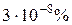 . Следовательно, лишь в указанных пределах точности (
. Следовательно, лишь в указанных пределах точности ( ) справедлив закон сохранения массы при реакции горения. Научившись взвешивать с такой точностью, мы сумели бы непосредственно обнаружить это изменение массы. Сейчас оно установлено только косвенным путем, так как нужной точности взвешивания мы не достигли.
) справедлив закон сохранения массы при реакции горения. Научившись взвешивать с такой точностью, мы сумели бы непосредственно обнаружить это изменение массы. Сейчас оно установлено только косвенным путем, так как нужной точности взвешивания мы не достигли.
В качестве другого примера можно указать, что повышение точности измерений плотности воды привело в 1982 г. к открытию тяжелого изотопа водорода – дейтерия, ничтожное содержание которого в обычной воде немного увеличивает ее плотность.
Наиболее важным примером является закон об изменении массы вещества при движении с большой скоростью:  , где
, где  – масса покоящегося тела,
– масса покоящегося тела, 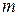 – масса движущегося тела со скоростью
– масса движущегося тела со скоростью  ,
, 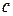 – скорость света. В силу малости
– скорость света. В силу малости 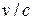 ко времени создания теории относительности
ко времени создания теории относительности 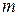 всегда было равно
всегда было равно  , так как недостаточная точность измерений не позволяла их различать. По мере увеличения точности измерений и перехода к большим скоростям такое изменение массы удалось наблюдать. Сейчас последнее соотношение имеет не только теоретический интерес, но и используется в инженерных расчетах. Из сказанного видно, как иногда важно стремиться к максимальному увеличению точности.
, так как недостаточная точность измерений не позволяла их различать. По мере увеличения точности измерений и перехода к большим скоростям такое изменение массы удалось наблюдать. Сейчас последнее соотношение имеет не только теоретический интерес, но и используется в инженерных расчетах. Из сказанного видно, как иногда важно стремиться к максимальному увеличению точности.
Понятие физической величины может утратить смысл, если к ее измерению предъявить неоправданно высокое требование точности. Так, например, не совсем ясно, о чем идет речь, когда ставиться задача измерения длины твердого стержня с точностью до размеров электрона или даже атома. Принципиально неограниченная точность измерения длин имеет смысл для абстрактных прямолинейных отрезков геометрии, а не для реальных тел, имеющих атомистическую структуру.
5. Системы единиц физических величин
Для каждой физической величины единицу измерения можно выбирать совершенно произвольно, независимо от других величин. Однако на практике в целях удобства поступают иначе. Произвольно выбирают единицы измерения только для нескольких (семи) физических величин. Эти величины и их единицы измерения называют основными. Единицы измерения всех остальных физических величин устанавливают на основании законов (формул), связывающих эти величины с основными. Такие величины и их единицы измерения называют производными.
Совокупность всех основных и производных единиц измерения физических величин называется системой единиц.
В нашей стране утверждена Международная система единиц – СИ (система интернациональная). Оновными физическими величинами СИ являются длина, масса, время, термодинамическая температура Кельвина, сила электрического тока, сила света и количество вещества. За основные единицы приняты соответственно следующие семь: метр (м), килограмм (кг), секунда (с), кельвин (К), ампер (А), кандела (кд) и моль (моль).
Ранее наряду с СИ применялась физическая система (СГС), основными единицами которой являются сантиметр (см), грамм (г) и секунда (с).
Единицы измерения любой производной физической величины можно выразить через основные (пользуясь формулами, связывающими производную величину с основными). Иначе говоря, любую физическую величину можно выразить в основных единицах измерения. Выражение физической величины в основных единицах измерения называется размерностью физической величины. Поясним это на примере работы А.
Единицей измерения работы является джоуль. Для определения размерности работы выразим работу через основные физические величины – путь 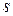 , массу
, массу 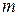 и время
и время  :
:  ,где
,где  – сила, а – ускорение. Подставив теперь в правую часть полученного равенства вместо основных физических величин их единицы измерения в СИ, получим размерность работы в этой системе:
– сила, а – ускорение. Подставив теперь в правую часть полученного равенства вместо основных физических величин их единицы измерения в СИ, получим размерность работы в этой системе:  . Результат определения размерности физической величины принято записывать условным равенством, в котором эта величина заключается в квадратные скобки. Применительно к нашему примеру это равенство записывается так:
. Результат определения размерности физической величины принято записывать условным равенством, в котором эта величина заключается в квадратные скобки. Применительно к нашему примеру это равенство записывается так: 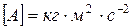 .
.
Размерности обеих частей физических величин должны быть одинаковыми. Это положение позволяет проверять правильность любых физических формул, в частности формул, получаемых при решении задач. Проверим, например, формулу пути 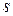 равномерно ускоренного движения:
равномерно ускоренного движения:  , где
, где 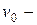 начальная скорость, а – ускорение:
начальная скорость, а – ускорение:
 ;
;  ;
; 
 .
.
Кроме того, размерность помогает глубже уяснить физический смысл формул и посредством размерностей можно даже выводить некоторые физические формулы с точностью безразмерного коэффициента.
Контрольные вопросы
1. В чем заключается фундаментальность физики?
2. Приведите примеры, свидетельствующие о связи физики с другими естественными науками и техникой.
3. В чем заключается суть физических исследований? Перечислите методы физических исследований и дополните их примерами.
4. В чем заключается сочетание экспериментальных и теоретических методов в познании окружающей среды?
5. Каким требованиям должны отвечать физические модели?
6. Что называется материальной точкой? Почему в механике вводят такую модель?
7. Какое значение имеет точность измерения физической величины?
8. Какие системы единиц измерения физических величин Вы знаете? Какова связь между ними?
Лекция №2. Кинематика материальной точки
при прямолинейном движении
Механика – исторически первый раздел физики, так как изучение остальных разделов физики невозможно без знания законов механики. Определения многих величин в других разделах, появившихся позже, являются обобщением механических величин. Например, закон Кулона в курсе электричества является обобщением закона всемирного тяготения.
Механика рассматривает простейшую форму движения – механическое движение, т.е. перемещение тел (или их частей) в пространстве относительно друг друга.
Механика подразделяется на кинематику, динамику и статику.
В кинематикерассматривают перемещение тел в зависимости от времени, не интересуясь причинами, которые вызывают движение или изменяют его. Динамика изучает законы движения тел под действием сил, его вызывающих. В статикеизучаются условия равновесия тел. Таким образом, статика является, по существу, частным случаем динамики, так как из динамики нам известны законы движения тел, а из статики можно вывести и законы покоя, равновесия тел. Однако в связи с большой практической значимостью статика выделяется в самостоятельный раздел механики.
1. Кинематические законы движения материальной точки
Рассмотрим механическое движение тел. Механическим движением тела называется изменение его положения в пространстве с течением времени.Механическое движение всегда относительно. Например, шарик, лежащий на столе, может быть описан расстоянием от него до стен или пола. При этом он относительно стола покоится. Но положение шарика можно определить и относительно Солнца или звезд. Ясно, что положение шарика будут определять другие расстояния. Эти расстояния будут меняться с течением времени, так как шарик вместе со столом вращается вокруг земной оси и обращается вокруг Солнца. Таким образом, положение тела может быть определено только по отношению к каким-либо другим телам. Эти тела называются телами отсчета или системой отсчета. Механическое движение есть изменение положения тела относительно тел отсчета. Никаких принципиальных преимуществ одной системы отсчета по сравнению с другой в кинематике указать нельзя. Все системы отсчета кинематически эквивалентны.
Для математического описания движения тел относительно выбранной системы отсчета задают систему координат, связанную с системой отсчета. Выбор системы координат определяется условием механической задачи. Например, если движение тела происходит вокруг тела, имеющего цилиндрическую или сферическую геометрию, удобно выбрать соответственно цилиндрическую или сферическую систему координат. Если движение происходит по плоскости и имеется центр симметрии, удобно использовать полярную систему координат. В общем случае наиболее удобна декартовая прямоугольная система координат, так как в ней все три координаты равноправны.
Кроме того, для описания движения необходимо отсчитывать время.
Как и всякая физическая величина, время количественно характеризуется некоторыми числами. Задача прежде всего состоит в том, чтобы выяснить, с помощью каких принципиальных измерительных операций эти числа могут быть получены. Тем самым устанавливается и точный смысл самих этих чисел.
Под временем в количественном смысле этого слова мы будем понимать показания каких-то часов. Точнее, надо говорить не о самом времени, а о промежутке времени между двумя событиями или моментами времени. Он характеризуется разностью показаний часов в рассматриваемые моменты времени. Когда говорят просто о времени, не указывая оба момента, являющиеся границами рассматриваемого промежутка времени, то предполагают, что один из этих моментов фиксирован и условно принят за начальный. От него и ведется отсчет времени. Часы здесь понимаются в более широком смысле слова, чем в обыденной жизни. Под часами понимают любое тело или систему тел, в которых совершается периодический процесс, служащий для измерения времени. Примерами таких процессов могут служить колебание – маятника с постоянной амплитудой, вращение Земли вокруг собственной оси относительно Солнца или звезд, колебания атома в кристаллической решетке, колебания электромагнитного поля, представляемого достаточно узкой спектральной линией, и пр. Так, если между двумя событиями Земля при вращении относительно звезд сделала один оборот, то говорят, что промежуток времени между этими двумя событиями составляет звездные сутки. Если при этом она совершила 10 оборотов, то соответствующий промежуток времени будет 10 звездных суток, и т.д. Если в течение звездных суток маятник совершил приблизительно 86 164 колебания, то говорят, что период одного колебания составляет одну секунду, и т.д. От звездных суток следует отличать солнечные сутки. Так называется промежуток времени, в течение которого Земля делает один оборот при вращении вокруг собственной оси относительно Солнца. Ввиду того, что Земля движется вокруг Солнца не по круговой, а по эллиптической орбите, это ее движение не совсем равномерно. Это значит, что солнечные сутки изо дня в день несколько изменяются в течение года. Поэтому при измерении времени пользуются так называемыми средними солнечными сутками. Они составляют 24 часа = 24 • 60 = 1440 минут = 1440 - 60 = 86 400 секунд.
К часам предъявляют требование, чтобы они шли «равномерно». Но что значит «часы идут равномерно»? Говорят, это означает, что периодический процесс, служащий для отсчета времени, должен повторяться через строго одинаковые промежутки времени. Однако это не есть ответ на вопрос, так как убедиться в одинаковости следующих друг за другом промежутков времени можно только в том случае, когда мы уже располагаем равномерно идущими часами. Выйти из этого логического круга можно только путем определения, так как никакого априорного представления о равномерном течении времени не существует. Надо условиться считать какие-то часы по определению равномерно идущими. Такие часы должны рассматриваться как эталонные или основные часы, по которым должны градуироваться все остальные.
В принципе любые часы могут быть приняты за эталонные. Однако так поступать не целесообразно. Эталонные часы должны быть достаточно «хорошими» и прежде всего обладать высокой воспроизводимостью. Это означает, что если изготовить с возможной тщательностью много «одинаковых» эталонных часов, то они с большой точностью должны идти одинаково, независимо от того, изготовлены ли они одновременно, или между моментами их изготовления прошло длительное время. Например, песочные часы дают несравненно худшую воспроизводимость, чем маятниковые часы.
Не так давно за основные или эталонные часы принимались «астрономические часы». Долгое время основными часами служила Земля, вращающаяся вокруг собственной оси относительно звезд, а основной единицей времени – сутки. Недавно вместо осевого вращения Земли стали пользоваться ее орбитальным движением вокруг Солнца, принимая за основную единицу времени тропический год, т.е. промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия. При измерении времени таким путем достигалась лучшая воспроизводимость. Но еще лучшая воспроизводимость была достигнута после изобретения кварцевых, молекулярных и атомных часов.
Все эти часы представляют довольно сложные радиотехнические устройства. Здесь нет необходимости останавливаться на принципах действия и деталях устройства таких часов. Достаточно заметить, что роль маятника или балансира, регулирующих ход часов, выполняют в кварцевых часах колебания кристаллической решетки кварца, в молекулярных часах – колебания атомов в молекулах, в атомных часах – колебания электромагнитного поля в узких спектральных линиях атомов некоторых изотопов химических элементов, находящихся в точно определенных и строго контролируемых внешних условиях. Особой стабильностью обладают последние из отмеченных колебаний. Поэтому период именно таких колебаний в настоящее время и принимается в качестве основной единицы времени, с помощью которой воспроизводится секунда. Конкретно, секунда – это промежуток времени, в течение которого совершается 9 192 631 770 колебаний электромагнитного излучения, соответствующего переходу между двумя определенными сверхтонкими уровнями основного состояния атома цезия-133 в отсутствие внешних полей.
С помощью кварцевых, молекулярных и атомных часов было показано, что Земля вокруг своей оси вращается «неравномерно».
Воспользуемся для описания движения точки декартовой прямоугольной системой координат, начало которой (точка О) связано с какой-либо системой отсчета (на рисунке обозначение осей  ) должно соответствовать «правой тройке».
) должно соответствовать «правой тройке».

| Рис.2.1. |
Положение точки А в данный момент времени по отношению к этой системе координат характеризуется тремя координатами х, у и z или радиусом-вектором  , проведенным из начала системы координат в данную точку (рис.2.1). Если точка движется, то каждому последующему моменту времени будут соответствовать новые значения координат х, у и z:
, проведенным из начала системы координат в данную точку (рис.2.1). Если точка движется, то каждому последующему моменту времени будут соответствовать новые значения координат х, у и z:

 (2.1)
(2.1)
Уравнения (2.1) называют скалярными кинематическими уравнениями движения или уравнениями движения материальной точки в параметрическом виде, где время служит в качестве параметра.Они определяют движение материальной точки координатным способом.
Координаты х, у и z являются проекциями радиуса-вектора  на координатные оси, а потому:
на координатные оси, а потому:
 , (2.2)
, (2.2)
где 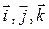 координатные орты, т.е. единичные векторы, направленные вдоль осей координат х, у и z.
координатные орты, т.е. единичные векторы, направленные вдоль осей координат х, у и z.
В любой момент времени длина радиуса-вектора определяется из выражения: 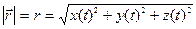 .
.
Зависимость  (2.3)
(2.3)
есть векторное кинематическое уравнение движения материальной точки.
Каждую из приведенных формул (2.1) и (2.3) называют также кинематическим законом движения материальной точки. Для полного описания движения точки достаточно знать кинематические законы движения.
2. Скорость и ускорение при прямолинейном движении
Линию, которую описывает материальная точка при своем движении в пространстве, называюттраекторией.В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Исключив из (2.4) или (2.7) время, можно определить уравнение траектории.
Расстояние, пройденное по траектории, называетсяпутем.Обозначается как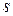 .Путь всегда выражается положительным числом. Поэтому пути, пройденные за отдельные промежутки времени, в течение которых материальная точка не изменяет направления своего движения, складываются арифметически.
.Путь всегда выражается положительным числом. Поэтому пути, пройденные за отдельные промежутки времени, в течение которых материальная точка не изменяет направления своего движения, складываются арифметически.
Отрезок прямой, проведенный из начального положения материальной точки в конечное, называется перемещением.Перемещение обозначается как 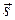 или
или .Кроме числового значения перемещение характеризуется также и направлением. Следовательно, перемещение – векторная величина. Поэтому перемещения складываются геометрически.
.Кроме числового значения перемещение характеризуется также и направлением. Следовательно, перемещение – векторная величина. Поэтому перемещения складываются геометрически.
Пусть материальная точка движется вдоль прямой линии. Примем эту прямую за координатную ось Х, поместив начало координат О в какой-то произвольной ее точке. Положение материальной точки в рассматриваемом случае определяется одной координатой:
 (2.4)
(2.4)
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина пути равна модулю перемещения, т.е.  .
.
Пусть в какой-то фиксированный момент времени материальная точка находится в положении  . В этот момент времени ее координата равна
. В этот момент времени ее координата равна 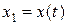 . В более поздний момент времени материальная точка переместится в положение
. В более поздний момент времени материальная точка переместится в положение 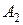 с координатой
с координатой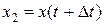 . За время
. За время  материальная точка проходит путь
материальная точка проходит путь  . Он считается положительным, если перемещение совершается вправо, и отрицательным, если перемещение совершается влево. Отношение пройденного пути
. Он считается положительным, если перемещение совершается вправо, и отрицательным, если перемещение совершается влево. Отношение пройденного пути 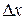 к промежутку времени
к промежутку времени  называется средней скоростью материальной точки за время
называется средней скоростью материальной точки за время  . Таким образом, по определению средняя скорость равна
. Таким образом, по определению средняя скорость равна
 (2.5)
(2.5)
Такое определение средней скорости имеет смысл для любых как угодно малых значений  , но отличных от нуля.
, но отличных от нуля.
Вообще, средняя скорость зависит не только от  , но и от
, но и от  . Теперь, оставляя момент времени
. Теперь, оставляя момент времени  неизменным, промежуток времени
неизменным, промежуток времени  будем брать все меньше и меньше, устремляя его к нулю. Тогда к нулю будет стремиться и пройденный путь
будем брать все меньше и меньше, устремляя его к нулю. Тогда к нулю будет стремиться и пройденный путь 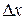 . Как показывает опыт, отношение
. Как показывает опыт, отношение  при этом будет стремиться к вполне определенному пределу, который может зависеть только от
при этом будет стремиться к вполне определенному пределу, который может зависеть только от  , но уже не будет зависеть от
, но уже не будет зависеть от  . Этот предел называется истинной или мгновенной скоростью материальной точки в момент времени
. Этот предел называется истинной или мгновенной скоростью материальной точки в момент времени  :
:
 (2.6)
(2.6)
В математике предел, определяемый формулой (2.6), называется производной функции 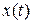 по аргументу
по аргументу  . Таким образом, по определению производной следует, что истинная или мгновенная скорость материальной точки
. Таким образом, по определению производной следует, что истинная или мгновенная скорость материальной точки  есть производная координаты
есть производная координаты  по времени, или производная пройденного пути s по времени:
по времени, или производная пройденного пути s по времени:
 (2.7)
(2.7)
Если за равные, сколь угодно малые промежутки времени материальная точка проходит одинаковые пути, движение материальной точки называется равномерным. Разделив путь s на время  , за который он пройден, получим величину
, за который он пройден, получим величину
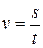 , (2.8)
, (2.8)
которую в обыденной жизни называют скоростью материальной точки. Она в данном случае совпадает с мгновенной скоростью.
Если движение неравномерное, величина, получаемая делением s на время  , дает среднее значение скорости за промежуток времени
, дает среднее значение скорости за промежуток времени  :
:
 (2.9)
(2.9)
Скорость материальной точки, вообще говоря, является функцией времени:  .
.
Зная мгновенную скорость, можно вычислить путь, пройденный материальной точкой от момента времени  до момента
до момента  по формуле
по формуле
 (2.10)
(2.10)
С учетом данного выражения можно получить формулу для средней скорости:
 (2.11)
(2.11)
Производная скорости по времени называется ускорением материальной точки. Ускорение мы обозначим через а. Таким образом, по определению ускорения
 , (2.12)
, (2.12)
или
 (2.13)
(2.13)
Производная (2.12) называется также второй производной координаты x или пути s по времени и обозначается символами
 (2.14)
(2.14)
В общем случае ускорение является функцией времени  .
.
При равноускоренном движении  .
.
В существовании производных координаты по времени убеждаемся опытным путем, а не путем логических рассуждений.
Контрольные вопросы
1. Что называется механическим движением? Перечислите свойства механического движения.
2. Что такое система отсчета?
3. Как выбрать систему координат?
4. Как определить точное время?
5. Что такое траектория? В чем отличие уравнения траектории от уравнения движения?
6. Что такое перемещение? Всегда ли модуль перемещения равен отрезку пути, пройденного точкой?
7. Дайте определение средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения.
8. Можно ли получить выражения для мгновенной скорости и мгновенного ускорения из кинематических уравнений движения?
9. Выясните физический смысл формулы (2.10), определяющей путь.
10. Выясните физический смысл средней скорости?
11. Начертите графики пути и скорости равномерного движения.
12. Начертите графики пути, скорости и ускорения материальной точки при равноускоренном движении.
13. Используя выражения (2.7) и (2.14), получите зависимости пути и изменения координаты от времени.
Лекция №3. Кинематика материальной точки
при криволинейном движении
1. Скорость материальной точки при криволинейном движении
Понятия скорости и ускорения естественным образом обобщаются на случай движения материальной точки по криволинейной траектории.
Пусть при своем движении материальная точка, занимавшая положение А в момент времени  , через некоторое время
, через некоторое время  оказалась в положении В.
оказалась в положении В.

 Z
Z


 B
B
 A
A 
r1
r2

 О y
О y
X
Рис.3.1.
Выберем декартовую систему координат. Пусть моменту времени  соответствует радиус-вектор
соответствует радиус-вектор  , а моменту времени
, а моменту времени 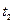 -
-  , тогда за промежуток времени
, тогда за промежуток времени  тело получит перемещение
тело получит перемещение
 (3.1)
(3.1)
Отношение перемещения 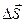 к промежутку времени
к промежутку времени  , за который это перемещение произошло, называется средней скоростью за промежуток времени от t до
, за который это перемещение произошло, называется средней скоростью за промежуток времени от t до  :
:
 (3.2)
(3.2)
Величина вектора средней скорости показывает, как быстро (в среднем) происходит перемещение точки, а его направление определяет, в какую сторону происходит перемещение.
Однако знание перемещения и средней скорости не дает достоверной информации о характере движения и виде траектории. Более детальное описание движения мы получим, если разделим путь на ряд последовательных перемещений. При уменьшении этих перемещений будет уменьшаться и величина промежутка времени, следовательно, отношение (3.2) будет стремиться к определенному пределу. Скоростью (точнее мгновенной скоростью) материальной точки в данной точке траектории в данный момент времени называется предел отношения (3.2) при  :
:
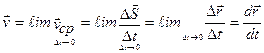 (3.3)
(3.3)
Из этого определения следует, что:
- скорость есть векторная величина;
- скорость в каждой точке траектории направлена по касательной к ней в ту сторону, куда движется точка;заметим, чтопри равномерном движении скорость, изменяясь как угодно по направлению, остается постоянной по модулю;
 |
Рис.3.2.
- 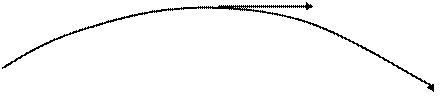
скорость представляет собой первую производную перемещения по времени;
- скорость является первой производной радиус-вектора по времени;
- величина скорости равна первой производной пути по времени;
- вектор скорости можно представить в виде
 , (3.4)
, (3.4)
или 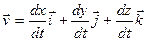 ; (3.5)
; (3.5)
- составляющие вектора скорости по координатным осям равны:
 ,
, 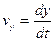 ,
, ,(3.6)
,(3.6)
т.е. скорости движения проекций точки вдоль координатных осей равны проекциям вектора скорости на соответствующие оси;
- величина скорости равна
 ; (3.7)
; (3.7)
- для нахождения закона движения по известной зависимости вектора скорости от времени необходимо интегрировать уравнения (3.3). Например, если известна скорость вдоль оси Ох, то закон движения вдоль этой оси имеет вид:
 (3.8)
(3.8)
где  – координата точки в начальный момент времени.
– координата точки в начальный момент времени.
Если движение равномерное, т.е. 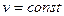 , то в силу выражения (3.8)
, то в силу выражения (3.8)
 (3.9)
(3.9)
2. Ускорение материальной точки при криволинейном движении
В общем случае (и чаще всего) при движении материальной точки скорость меняется как по величине, так и по направлению. Пусть в момент времени 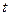 материальная точка двигалась со скоростью
материальная точка двигалась со скоростью  , а при
, а при  – скоростью
– скоростью  . Перенесем начало вектора скорости
. Перенесем начало вектора скорости  из точки В в точку А, сохраняя величину и направление вектора
из точки В в точку А, сохраняя величину и направление вектора  . Тогда приращение скорости
. Тогда приращение скорости  (рис.3.3).
(рис.3.3).


 Δυτ
Δυτ




 υ1
υ1

 A
A


 Δv
Δv
 |
ΔS

 B
B
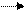
 Δυn υ2
Δυn υ2
 υ2
υ2
Рис. 3.3.
Среднее ускорение на отрезке траектории между А и В:
 (3.10)
(3.10)
Величина вектора среднего ускорения показывает, как быстро (в среднем) происходит изменение скорости точки, а направление его совпадает с направлением вектора изменения скорости, т.е. направлено под углом к траектории в сторону её вогнутости.
Однако знание перемещения и средней скорости не дает достоверной информации о характере движения в данной точке пространства. Поэтому нужно уменьшить промежуток времени. При его уменьшении будет уменьшаться и величина вектора приращения скорости, следовательно, отношение (3.10) будет стремиться к определенному пределу. Ускорением (точнее мгновенным ускорением) материальной точки в данной точке траектории в данный момент времени называется предел отношения (3.10) при  :
:
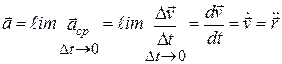 (3.11)
(3.11)
Из этого определения следует, что:
- ускорение есть векторная величина;
- ускорение направлено под углом к траектории в сторону её вогнутости;
- ускорение представляет собой первую производную вектора скорости по времени;
- ускорение представляет собой вторую производную радиус-вектора по времени;это следует из формул (3.11) и (3.3);
- вектор ускорения можно представить в виде
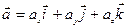 , (3.12)
, (3.12)
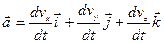 , (3.13)
, (3.13)
или  ; (3.14)
; (3.14)
- составляющие вектора скорости по координатным осям равны:
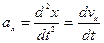 ,
, 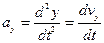 ,
, ;(3.15)
;(3.15)
- величина ускорения равна 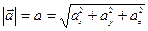 ; (3.16)
; (3.16)
- для нахождения закона движения необходимо найти проекцию ускорения на оси координат по известным зависимостям проекций вектора скорости от времени, а затем интегрировать левую половину уравнений (3.15);
- направление вектора ускорения совпадает с направлением вектора скорости только в случае ускоренного (или замедленного) прямолинейного движения.
Закон движения материальной точки находится из решения уравнений (3.15). Для примера рассмотрим равноускоренное прямолинейное движение, т.е.  , где изменяется только скорость:
, где изменяется только скорость:  , где
, где 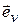 – единичный вектор скорости.
– единичный вектор скорости.
Из этого выражения следует, что в случае увеличения со временем скорости (т.е.  ), ускорение направлено так же, как скорость, а модуль ускорения равен
), ускорение направлено так же, как скорость, а модуль ускорения равен  . Если же скорость со временем уменьшается (т.е.
. Если же скорость со временем уменьшается (т.е. 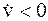 ), направление ускорения противоположно направлению скорости, а модуль ускорения равен
), направление ускорения противоположно направлению скорости, а модуль ускорения равен  .
.
Пусть движение происходит равноускоренно вдоль оси Ох, т.е. движение равноускоренное и прямолинейное. Тогда из первого уравнения (3.15) имеем:

Рассмотрим подробнее, как меняется скорость при криволинейном движении. Пусть материальная точка за некоторый промежуток времени  перемещается из положения А в положение В с изменением скорости от
перемещается из положения А в положение В с изменением скорости от 
 до
до  . Перенесем вектор
. Перенесем вектор  параллельно самому себе так, чтобы его начало совпало с точкой А. Соединим концы векторов
параллельно самому себе так, чтобы его начало совпало с точкой А. Соединим концы векторов 
 и
и  . Тогда приращение векторов скорости равно
. Тогда приращение векторов скорости равно  . Отложим на векторе
. Отложим на векторе  вектор, равный вектору
вектор, равный вектору  . Следовательно, вектор
. Следовательно, вектор  можно рассматривать как сумму двух составляющих: как показано на рисунке, обозначим их
можно рассматривать как сумму двух составляющих: как показано на рисунке, обозначим их 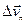 и
и 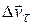 , т.е.
, т.е. 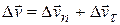 . Тогда среднее ускорение равно
. Тогда среднее ускорение равно  .
.
Используя (3.11), из последнего выражения получим:
 , (3.17)
, (3.17)
где  и
и  – соответственно нормальное и тангенциальное ускорения. Причем в пределе направления
– соответственно нормальное и тангенциальное ускорения. Причем в пределе направления 
 и
и  практически совпадают, следовательно, вектор
практически совпадают, следовательно, вектор  направлен так же, как и вектор
направлен так же, как и вектор  по касательной в каждой точке траектории, а его значение определяют изменения величины (модуля) скорости:
по касательной в каждой точке траектории, а его значение определяют изменения величины (модуля) скорости:
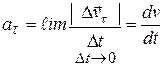 (3.18)
(3.18)
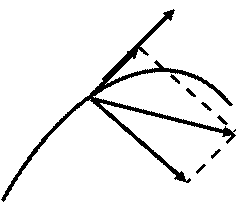
Нормальная составляющая ускорения  при этом окажется перпендикулярной вектору скорости
при этом окажется перпендикулярной вектору скорости  , направленному перпендикулярно касательной к траектории, и показывать изменение направления скорости (рис. 3.4).
, направленному перпендикулярно касательной к траектории, и показывать изменение направления скорости (рис. 3.4).
 |
V

ατ
 |
α
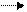 αn
αn
Рис.3.4
Величина (модуль) полного ускорения при его разложении на нормальную и тангенциальную составляющие равна:
 (3.19)
(3.19)
3.Ускорение при движении материальной точки по окружности
Пусть точка движется равномерно по окружности радиуса  с постоянной по величине во времени скоростью. Движение точки является криволинейным. Поэтому при равномерном движении точки по окружности должно существовать нормальное ускорение, обуславливающее изменение направления скорости.
с постоянной по величине во времени скоростью. Движение точки является криволинейным. Поэтому при равномерном движении точки по окружности должно существовать нормальное ускорение, обуславливающее изменение направления скорости.
Если материальная точка за некоторый промежуток времени  перемещается из положения А в положение В с изменением скорости от
перемещается из положения А в положение В с изменением скорости от 
 до
до  , то приращение скорости за это время равно
, то приращение скорости за это время равно  (рис. 3.5).
(рис. 3.5).

 A v1
A v1
 |  |
S =∆r
R
 v1
v1
О B D
 R∆v
R∆v
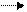 C v2
C v2
Рис. 3.5.
Перенесем вектор  параллельно самому себе так, чтобы его начало совпало с точкой В. Рассмотрим треугольники АОВ и СВД. Они подобны, так как ÐАОВ =ÐСВД и эти треугольники являются равнобедренными (ОА=ОВ=R , ВС=ВД=
параллельно самому себе так, чтобы его начало совпало с точкой В. Рассмотрим треугольники АОВ и СВД. Они подобны, так как ÐАОВ =ÐСВД и эти треугольники являются равнобедренными (ОА=ОВ=R , ВС=ВД= . Поэтому составим пропорцию:
. Поэтому составим пропорцию:  . Отсюда
. Отсюда 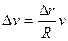 . Найдем ускорение точки. Разделим обе части последнего равенства на
. Найдем ускорение точки. Разделим обе части последнего равенства на  и перейдем к пределу при
и перейдем к пределу при  . Таким образом,
. Таким образом,
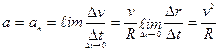 (3.20)
(3.20)
Итак, при движении точки по окружности её нормальное ускорение зависит от скорости точки и от радиуса окружности. Оно направлено по радиусу к центру окружности и поэтому его называют центростремительным ускорением.
Для любого положения движущейся точки можно написать  , где
, где  – единичный вектор нормали к круговой траектории движущейся точки, направленный к центру окружности.
– единичный вектор нормали к круговой траектории движущейся точки, направленный к центру окружности.
Если точка движется по окружности неравномерно, то вектор скорости меняется и по величине, и по направлению. В этом случае существуют и тангенциальное и нормальное ускорения. Следовательно, полное ускорение направлено под углом к радиусу. Так как нормальное ускорение связано с изменением только направления вектора скорости, то и в случае неравномерного движения по окружности оно выражается формулой (3.20).
Рассмотрим движение точки по произвольной криволинейной траектории. Из геометрии известно, что небольшой её участок (рис.3.6) всегда можно заменить дугой окружности некоторого радиуса 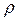 . Такая окружность называется кругом кривизны траектории в данной точке. Радиус его называется радиусом кривизны, величина, обратная ему, – кривизной.
. Такая окружность называется кругом кривизны траектории в данной точке. Радиус его называется радиусом кривизны, величина, обратная ему, – кривизной.

ρ
ρ
ρ
Рис. 3.6.
При этом для нормального ускорения формула (3.20) сохраняется, но под радиусом окружности следует подразумевать радиус кривизны траектории. Таким образом, величина вектора полного ускорения при криволинейном движении определяется выражением:
 (3.27)
(3.27)
4. Кинематика вращательного движения материальной точки
Введенные выше кинематические законы движения достаточны для описания любого вида движения материальной точки. Однако в случае вращательного движения удобнее пользоваться понятиями угловой скорости и углового ускорения.
Рассмотрим простейший случай движения материальной точки по окружности радиуса R . Выберем на окружности некоторую точку О! в качестве начала отсчета и проведем в неё из центра окружности радиус ОО! (рис.3.7).

O!
А
R
А!
φ 
O
Рис. 3.7.
Положение точки А, движущейся на окружности, в некоторый момент времени можно определить при помощи угла  который составляет радиус ОА, проведенный к точке с начальным радиусом ОО1. Тогда закон движения точки может быть выражен функцией:
который составляет радиус ОА, проведенный к точке с начальным радиусом ОО1. Тогда закон движения точки может быть выражен функцией: 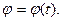
Пусть через некоторый промежуток времени  точка оказалась в положении А1, и угол
точка оказалась в положении А1, и угол  при этом изменился на величину
при этом изменился на величину  . Быстрота изменения угла
. Быстрота изменения угла  с течением времени определяется как предел, к которому стремится отношение
с течением времени определяется как предел, к которому стремится отношение  , если промежуток времени
, если промежуток времени  стремится к нулю, т.е.
стремится к нулю, т.е.
 (3.28)
(3.28)
Единицей измерения угловой скорости является радиан в секунду (рад/с или 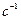 ). Рад/с – угловая скорость равномерно вращающегося тела, при которой за время 1 с совершается поворот тела относительно оси на угол 1 рад.
). Рад/с – угловая скорость равномерно вращающегося тела, при которой за время 1 с совершается поворот тела относительно оси на угол 1 рад.
Угловым ускорением называют величину, характеризующую быстроту изменения угловой скорости:
 (3.29)
(3.29)
С учетом (3.28) также имеем:
 (3.30)
(3.30)
При малом угле поворота связь между линейным 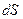 и угловым перемещением
и угловым перемещением  можно выразить соотношением:
можно выразить соотношением: 
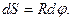
Исходя из этого выражения, легко устанавливается связь между линейной скоростью v (скорость точки вдоль траектории) и угловой скоростью 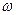 . Для этого достаточно разделить последнее выражение на
. Для этого достаточно разделить последнее выражение на 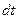 :
: 
Отсюда, в силу формул (3.3) и (3.28), имеем
 (3.31)
(3.31)
Аналогично получим связь тангенциального ускорения (а не нормального!) с угловым:

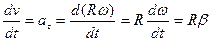 (3.32)
(3.32)
А для определения величины нормального ускорения воспользуемся формулой :  . Тогда
. Тогда  .
.
Заметим, что при движении материальной точки по окружности, т.е. при вращательном движении, радиус-вектор  направлен от центра по радиусу окружности
направлен от центра по радиусу окружности 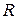 , формулу для центростремительного (или нормального) ускорения можно записать в векторной форме
, формулу для центростремительного (или нормального) ускорения можно записать в векторной форме  .
.
Знак минус указывает на то, что направления векторов  и
и  взаимно противоположны, т.е. ускорение
взаимно противоположны, т.е. ускорение  направлено к центру круговой траектории, по которой вращается материальная точка.
направлено к центру круговой траектории, по которой вращается материальная точка.
Время одного полного оборота называется периодом Т. Тогда угловая скорость  , т.е.
, т.е. 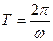 , частота n
, частота n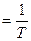 .
.
Контрольные вопросы
1. Дайте определение средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения. Каковы их направления?
2. Что характеризуют тангенциальная и нормальная составляющие ускорения? Каковы их модули?
3. Возможны ли движения, при которых отсутствуют нормальное и тангенциальное ускорения? Приведите примеры.
4. Что называется угловой скоростью и угловым ускорением?
5. Какова связь между линейными и угловыми величинами?
6. Выведите уравнения движения и формулу скорости для равноускоренного и равнозамедленного движений (с начальной и без начальной скорости).
7. Постройте графики скорости равномерного, равноускоренного и равнозамедленного движений.
8. Как движется тело, брошенное вертикально вверх?
9. Сформулируйте принцип независимости движений.
10. Дан вектор скорости тела в некоторый момент времени. Можно ли определить ускорение тела в этот момент?
11. Между точками А и В движется по прямой тело таким образом, что, выходя из точки А с нулевой начальной скоростью, оно должно иметь в точке В скорость, равную рулю. При этом тело может двигаться равномерно или с постоянным по модулю ускорением а. Каким должен быть характер движения, чтобы время его было минимальным?
12. Определите, на какую величину путь, пройденный свободно падающим телом в n-ую секунду, больше пути, пройденного в предыдущую секунду?
13. С некоторой высоты падает коробка, в центре которой находится металлический шарик, не соприкасающийся с ее стенками. Определите движение шарика относительно стенки коробки во время падения. Сопротивление воздуха не учитывать.
14. Как изменяются время и дальность полета тела, брошенного горизонтально, при увеличении высоты его подъема в четыре раза? Скорость бросания при этом не изменяется.
15. Под каким углом к горизонту надо бросить тело, чтобы наибольшая высота подъема была равна дальности полета? Считать, что на тело действует попутный ветер, сообщающий ему горизонтальное ускорение.
16. Под некоторым углом к горизонту из шланга бьет струя воды. Почему восходящая ветвь струи сплошная, а нисходящая рассыпается на отдельные части?
Лекция №4. Динамика материальной точки
Динамика– раздел механики, в котором изучаются законы движения тел в связи с вызывающими его физическими причинами. Основные положения динамики точки были сформулированы И. Ньютоном в его «Математических началах натуральной философии» в 80-х годах 17 века в виде трех законов движения. Законы Ньютона возникли в результате обобщения большого количества наблюдений и экспериментов. Правильность их подтверждается соответствием с опытом тех следствий, которые из них вытекают.
Первый шаг в понимании движения был сделан Г.Галилеем, когда он открыл впервые свой принцип инерции: тело, предоставленное самому себе, если на него не действует никакая сила, сохраняет свое прямолинейное движение с постоянной скоростью, как двигалось до этого, или остается в покое, если оно до этого покоилось. Конечно, в природе такого не бывает. Например, шарик, катящийся по поверхности стола, останавливается за счет силы трения.
Естественным является вопрос: как движется тело, почему оно движется так, а не иначе, какие причины вызывают или изменяют это движение. На эти вопросы ответ дал И.Ньютон, сформулировав три закона.
1. Первый закон Ньютона
Этот закон Ньютон сформулировал следующим образом:
Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не выведет его из этого состояния.
Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией.Поэтому этот закон в современной формулировке гласит следующее.
Существуют такие системы отсчета, в которых всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной. Поэтому и называется первый закон законом инерции. Инерциальных систем отсчета множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, т.е. поступательно с постоянной скоростью является инерциальной. Чтобы убедиться в этом, рассмотрим движение материальной точки относительно систем отсчета К и 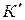 (рис.4.1) . Допустим, что система
(рис.4.1) . Допустим, что система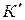 движется относительно системы К поступательно с постоянной скоростью
движется относительно системы К поступательно с постоянной скоростью  . Как видно из рисунка, между радиус-векторами имеется соотношение
. Как видно из рисунка, между радиус-векторами имеется соотношение
 .
.
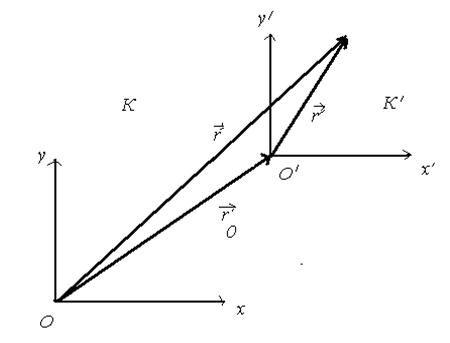
Рис. 4.1.
Продифференцировав его по времени, найдем, что  , т.е.
, т.е.  .
.
Если на материальную точку не действуют никакие тела и система инерциальна, то скорость материальной точки в этой системе будет постоянной. Из последней формулы следует, что скорость материальной точки  в системе
в системе 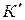 также оказывается постоянной. Это означает, что система
также оказывается постоянной. Это означает, что система 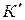 также инерциальна.
также инерциальна.
Установить, является ли данная система инерциальной или нет, можно опытным путем. Например, опыт показывает, что с большой степенью точности систему отсчета, связанную с Землей (геоцентрическая система отсчета) при изучении явлений, происходящих на Земле, можно считать инерциальной.
С гораздо большей точностью можно считать инерциальной систему отсчета, в которой начало координат совмещено с Центром Солнца, а координатные оси направлены на три неподвижные звезды, сохраняющие с известной точностью неизменное положение на небесном своде (гелиоцентрическая система отсчета). Она является инерциальной при описании явлений, происходящих в солнечной системе, а не в галактике.
Очевидно, первый закон является приближенным законом.
Во-первых, нет и не может быть ни с чем не взаимодействующих тел. Чем меньше это взаимодействие, тем точнее выполняется первый закон. Например, если ударить ногой по мячу, то он после падения по траве продвинется значительно меньше, чем по асфальту, по которому он катится десятки метров, не снижая своей скорости. Это расстояние зависит, во-первых, от силы удара ноги, и, во-вторых, от шероховатости поверхности. Лишь считая, что поверхность идеально гладкая и воздействие на тело других тел в вертикальном направлении отсутствует, можно сделать вывод о справедливости первого закона Ньютона.
Во-вторых, зависит от выбора тела отсчета. Например, на перроне лежит камень. Он находится в покое относительно перрона, т.е. инерциальной системы отсчета. Однако для наблюдателя, которое смотрит на камень из окна трогающегося поезда, камень движется ускоренно, хотя ясно, что никаких новых воздействий на камень при трогании с места не появилось. Ускоренное движение камня относительно поезда нельзя объяснить воздействием какого-либо тела. В этом случае первый закон не выполняется относительно системы отсчета, связанной с поездом.
2. Масса
Опыт показывает, что при одинаковом воздействии различные тела по-разному изменяют скорость и получают различные ускорения. Это свойство тел влиять на величину собственного ускорения называется инертностью тел. Следовательно, величина ускорения, приобретаемого телом, зависит от некоторого собственного свойства тела. Это свойство тела характеризуют физической величиной, называемой массой.
Таким образом, масса – мера инертности тела. Под инертностью понимают неподатливость тела действию сил, т.е. свойство тела противиться изменению скорости под воздействием силы. В дальнейшем увидим также, что масса характеризует и гравитационные свойства тел и их энергосодержание.
Масса – скалярная величина. Следовательно, массы тел складываются алгебраически.
Масса составного тела равна сумме масс составляющих тел. Это свойство называется аддитивностью массы.
Массы 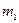 и
и  двух тел обратно пропорциональны ускорениям
двух тел обратно пропорциональны ускорениям  и
и  , которые эти тела приобретают под действием одной и той же силы, т.е.
, которые эти тела приобретают под действием одной и той же силы, т.е. 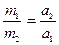 .
.
Поэтому масса тел определяется путем сравнения с массой некоторого произвольно выбранного эталонного тела. По международному соглашению таким эталоном является платино-иридиевый цилиндр, хранящийся в Париже и называемый килограммом массы (кг). Эта масса принята за единицу массы – 1 кг. Тысячная доля кг называется граммом массы (г). С высокой степенью точности масса 1 см3 дистиллированной воды при 4 0С равна 1 г.
При малых скоростях, т.е. таких, с которыми имеют дело в классической механике, масса – постоянная величина. Однако для тел, движущихся со скоростью, близкой к скорости света, масса зависит от скорости:
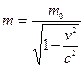 ,
,
где 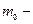 масса тела при
масса тела при 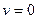 (масса покоя),
(масса покоя),  – скорость тела,
– скорость тела,  – скорость света, равная 3·
– скорость света, равная 3· м/с.
м/с.
Эта формула была получена А.Эйнштейном в 1905 г. Она показывает, что масса возрастает с увеличением скорости. В современных ускорителях электроны разгоняются до таких скоростей, при которых их масса возрастает в тысячи раз. Последняя формула также показывает, что тело не может иметь скорость, превышающую скорость света (в пустоте). По мере увеличения скорости тела растет и его масса, а ускорение уменьшается.
3. Сила
Согласно первому закону Ньютона, если на тело действуют другие тела, то состояние движения тела изменяется, т.е. изменяется его скорость и появляется ускорение. Количественной мерой воздействия на данное тело со стороны другого тела является сила.
Из определения следует, что понятие сила относится к двум телам. Если имеется сила, всегда можно указать тело, на которое она действует, и тело, со стороны которого она действует.
Общие свойства сил устанавливаются при рассмотрении особенностей влияния воздействия на ускорение. Они заключаются в следующем.
1. Так как ускорение является вектором, то и сила, вызывающая ускорение тела, является вектором, т.е. характеризуется и величиной, и направлением. Если силу обозначить через  , то:
, то:
- вектор силы можно представить в виде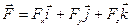 , где
, где  – составляющие вектора силы по координатным осям;
– составляющие вектора силы по координатным осям;
- величина силы равна
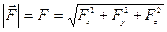 (4.1)
(4.1)
2. Ускорение тела, подвергающегося воздействию, зависит:
- от свойств этого тела (например, деревянный шарик катится мимо магнита равномерно по прямой, а стальной шарик – по кривой траектории);
- от свойств тела, оказывающего воздействие (например, стальной шар катится по кривой траектории вблизи магнита, а вблизи деревянного магнита – прямолинейно);
- от расстояния между телами, подвергающимися и оказывающими воздействие (чем ближе стальной шар подходит к магниту, тем больше искривляется траектория шарика);
- от относительной скорости взаимодействующих тел.
Сила, являясь характеристикой взаимодействия тел, также может зависеть от указанных особенностей.
Сила проявляется и в деформации тел. Например, груз, висящий на проволоке, растягивает её. По величине деформации можно определить величину силы. На этом основано измерение силы пружинным динамометром.
4. Второй закон Ньютона
Второй закон Ньютона гласит: ускорение 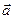 , приобретаемое телом под действием силы
, приобретаемое телом под действием силы  , направлено так же, как и сила, а по величине пропорционально силе и обратно пропорционально массе
, направлено так же, как и сила, а по величине пропорционально силе и обратно пропорционально массе  тела:
тела: 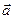 ~
~ .
.
Из последнего соотношения следует, что  ~
~ . Вводя коэффициент пропорциональности к, получим
. Вводя коэффициент пропорциональности к, получим
 (4.2)
(4.2)
Коэффициент  зависит от выбора системы единиц. Во всех используемых в настоящее время системах единиц полагается
зависит от выбора системы единиц. Во всех используемых в настоящее время системах единиц полагается 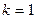 . Таким образом, из (4.2) имеем
. Таким образом, из (4.2) имеем
 (4.3)
(4.3)
Выражение (4.3) и представляет собой одну из формулировок второго закона Ньютона: произведение массы материальной точки на ее ускорение равно силе, действующей на материальную частицу.
Если же на тело одновременно действуют несколько сил, то сила  называется результирующей или равнодействующей силой.Она определяется как геометрическая сумма всех этих сил:
называется результирующей или равнодействующей силой.Она определяется как геометрическая сумма всех этих сил:  , где n – номер силы. Это и есть принцип суперпозиции.
, где n – номер силы. Это и есть принцип суперпозиции.
Следует отметить, что сформулированный выше второй закон, вообще говоря, применим к движению не произвольного тела, а материальной точки. Однако особо точные измерения движения планет вокруг Солнца показали, что он справедлив и для любого тела.
Заметим также, что второй закон Ньютона возник в результате обобщения огромного количества опытных данных. Следовательно, этот закон является экспериментальным.
Из второго закона Ньютона можно выделить следующие особенности движения материальной точки.
1. Силами определяется ускорение тела, а не скорость тела. Скорость тела зависит от предыдущего движения тела. Однако направление изменения скорости совпадает с направлением действия силы.
2. В инерциальных системах отсчета для каждой силы можно указать тело, со стороны которого эта сила действует на данное тело.
3. Если на тело не действуют силы или они скомпенсированы в любой момент времени (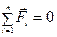 ), то
), то  и, следовательно, тело движется равномерно, т.е. выполняется первый закон Ньютона.
и, следовательно, тело движется равномерно, т.е. выполняется первый закон Ньютона.
4. Второй закон Ньютона эквивалентно трем скалярным уравнениям:
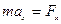 ,
,  ,
,  , (4.4)
, (4.4)
где  – проекции вектора ускорения на три оси декартовой системы координат,
– проекции вектора ускорения на три оси декартовой системы координат,  – проекции векторов сил на эти же оси.
– проекции векторов сил на эти же оси.
5. Если рассматривается движение системы тел, то второй закон применяется к каждому телу этой системы в отдельности с учетом всех сил, действующих на данное тело.
6. Уравнение (4.3) называется уравнением движения. Оно позволяет по известным силам, значениям координат и проекций скорости материальной точки в данный момент времени предсказать дальнейшее её движение.
7. Используя второй закон Ньютона, можно определить единицу измерения силы. В международной системе единиц сила измеряется в ньютонах Н. 1 Н = кг·м/с3. 1 Н равен силе, под действием которой тело массой 1 кг получает ускорение 1 м/с2. В системе СГС сила измеряется в динах. 1 дин = г·см/с2, т.е. это сила, под действием которой тело массой 1 г получает ускорение 1 см/с2. 1 Н = 105 дин. Иногда приходится пользоваться старыми приборами, где в качестве единицы измерения силы используется килограмм-сила 1 кГ: 1 кГ = 9,8 Н. Физический смысл её: 1 кГ – это сила, сообщающая телу массой 1 кг ускорение, равное 9,8 м/с2.
5. Третий закон Ньютона
Любое действие тел друг на друга носит характер взаимодействия: если первое тело действует на второе тело, сообщая ему ускорение, то всегда одновременно второе тело действует на первое тело, сообщая ему ускорение. Например, груз, давящий на опору, испытывает давление со стороны опоры. Соотношение между силами, приложенными к взаимодействующим телам, описывается третьим законом Ньютона: два взаимодействующих тела действуют друг на друга с силами, равными по величине и противоположными по направлению:
 , (4.5)
, (4.5)
где 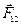 – сила, действующая на первое тело со стороны второго,
– сила, действующая на первое тело со стороны второго, 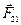 – сила, действующая на второе тело сто стороны первого.
– сила, действующая на второе тело сто стороны первого.
Например, гиря, лежащая на ладони, действует на ладонь силой 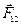 , направленной вниз, а гиря, в свою очередь, действует на ладонь силой
, направленной вниз, а гиря, в свою очередь, действует на ладонь силой 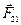 , направленной вниз. Равенство (4.5) имеет место независимо от того, покоится или движется ладонь с грузом.
, направленной вниз. Равенство (4.5) имеет место независимо от того, покоится или движется ладонь с грузом.
Особенности этого закона следующие.
- В нем речь идет о силах, приложенных к различным телам. Поэтому эти силы не могут уравновешивать друг друга.
- Результат действия сил, вследствие чего тела приобретают ускорения, зависит от массы каждого из взаимодействующих тел. Действительно, из (4.5) следует, что  или
или 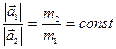 , где
, где 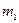 и
и  – массы взаимодействующих тел.
– массы взаимодействующих тел.
- Силы возникают попарно: всякой силе, приложенной к телу, можно всегда сопоставить равную по величине и противоположную по направлению силу, приложенную к другому телу, взаимодействующим с данным.
- Этот закон является приближенным, так как скорость взаимодействия тел – конечная величина. Это особенно важно в случае, когда взаимодействие осуществляется через поле.
6. Импульс. Общая формулировка второго закона Ньютона
Иногда требуется знать значения движущей силы, массы и ускорения тела для любого наперед заданного момента времени. Для такого рода расчетов применяется общая (или новая) формулировка второго закона Ньютона.
Пусть в течение некоторого промежутка времени 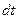 на тело массой
на тело массой  подействовала постоянная сила
подействовала постоянная сила  . Она будет сообщать телу постоянное ускорение
. Она будет сообщать телу постоянное ускорение 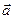 . Тогда уравнение движения этого тела преобразуется к виду
. Тогда уравнение движения этого тела преобразуется к виду
 , (4.6)
, (4.6)
если масса тела во время движения остается постоянной.
Импульсом (или количеством движения) материальной точки называют вектор 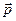 , равный по величине произведению массы
, равный по величине произведению массы  этой точки на её скорость
этой точки на её скорость  и совпадающий по направлению с направлением скорости, т.е.
и совпадающий по направлению с направлением скорости, т.е.
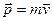 (4.7)
(4.7)
Тогда уравнение (4.6) приобретает вид:
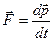 (4.8)
(4.8)
Уравнение (4.8) называется общей формой записи второго закона Ньютона. Он формулируется так: производная импульса тела (материальной точки) по времени равна равнодействующей силе, действующей на это тело.
Произведение движущей силы на время её действия называется импульсом силы. Поэтому уравнение (4.8) можно переписать в виде
 , (4.9)
, (4.9)
т.е. изменение импульса тела за некоторый промежуток времени равно изменению импульса силы, действующей на тело, за то же время и направлено в ту же сторону, куда направлен импульс силы. Такую формулировку второму закону динамики дал сам Ньютон.
Общая форма записи второго закона Ньютона верна и для переменной массы, например, она позволяет рассчитать движение ракет, масса которых изменяется вследствие выброса газов. В этом случае уравнение (4.8) записывается в виде
 (4.10)
(4.10)
7. Виды взаимодействий тел
Из кинематики известно, что знание величины и направления ускорения позволяет вычислить значения радиуса – вектора материальной точки в любой последующий момент времени. Законы динамики позволяют сделать это, если известна правая часть уравнений (4.3) или (4.4). Другими словами, нужно уметь определять силы, действующие на тело, положение которого требуется описать. Взаимодействие между макроскопическими телами физика сводит к взаимодействию между элементарными частицами. Таких элементарных частиц в настоящее время известно более сотни. Среди них наиболее популярны электрон, протон и нейтрон. Для характеристики всех частиц вводятся такие понятия, как масса покоя, электрический заряд, собственный механический момент (спин), а также четность, странность, красивость, барионный заряд, цветовой заряд, слабый заряд и т.д. Установлено, что между элементарными частицами существует четыре фундаментальных взаимодействия: сильное, слабое, электромагнитное и гравитационное (таблица 4.1).
Таблица 4.1.
| Название взаимодействия | Относительная интенсивность | Частица, «переносящая» взаимодействие | Характеристика частицы |
| Сильное | p-мезоны (глюоны) (8 типов) | m~250 mэлектр разнообразные | |
| Электромагнитное | 10-2 | фотон | E= hn |
| Слабое | 10-13 | W-частицы Z-частицы | Е~102 с2 m протон гипотетичны |
| Гравитационное | 10-40 | гравитон | гипотетичен |
В классической физике считается, что электромагнитное и гравитационное взаимодействия осуществляются посредством поля. Как было указано на первой лекции, поле – это особый вид материи, характерный тем, что каждой точке пространства можно приписать определенное значение поля. Физическое поле – непрерывно. Однако современная физика, базирующаяся на квантовых представлениях, считает дискретнойлюбую физическую величину, которая может изменяться только определенными порциями – квантами. Она приписывает полям дискретный характер, когда изменение поля рассматривается как излучение или поглощение некой частицы, распространяющейся с конечной скоростью (не больше скорости света с). Другими словами, в квантовой физике взаимодействия сводятся к обмену теми или иными частицами, переносящими квант действия. Если квант действия электромагнитного поля хорошо известен под названием фотон,то квант гравитационного взаимодействия остается по сих пор неоткрытым, хотя он уже получил название гравитона.
Сильное взаимодействие может объяснить наличиеядерных сил, ответственных за устойчивость атомного ядра. Ядерные взаимодействия обеспечивают связь частиц внутри ядер и приводят к взаимным превращениям тяжелых элементарных частиц (протонов, нейтронов, мезонов) при их столкновениях и самопроизвольном распаде. Радиус действия ядерного и слабого взаимодействий составляет менее 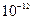 см.
см.
Слабые взаимодействия возникают между микрочастицами, обладающими так называемым слабым зарядом. Они ответственны за распад элементарных частиц. До 1983 года этот тип взаимодействия рассматривался только теоретиками, но в этом году экспериментально была открыта W+-частица с энергией 81 ГэВ (Гига – 109, электрон – Вольт – единица измерения энергии, равная 1,6•10 -19 Дж), так что слабое взаимодействие получило опытное подтверждение.
Из таблицы 4.1 видно, что гравитационные силы являются слабейшими из всех фундаментальных взаимодействий, однако они обладают свойствами аддитивности и достигают значительных величин в космическом масштабе (притяжение Луны, строение Солнечной системы и т.п.).
Электромагнитные взаимодействия осуществляются в телах, имеющих электрические заряды. В атомах, молекулах, твердых и жидких телах, в живых организмах именно электромагнитные взаимодействия являются главными. Проявляются они в виде силы трения, силы упругости, силы мышц.
8. Гравитационные силы (силы тяготения)
Изучая движение небесных тел и падение тел в земных условиях, И.Ньютон установил закон всемирного тяготения, который гласит: тело массой 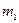 действует на находящееся от него на расстоянии r тело массой
действует на находящееся от него на расстоянии r тело массой 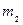 с силой
с силой 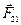 , величина которой пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними, т.е.
, величина которой пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними, т.е.
 (4.10)
(4.10)
В формуле (4.10)  называется гравитационной постоянной.
называется гравитационной постоянной.
Сила 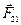 направлена по линии, соединяющей тела, и является силой притяжения.
направлена по линии, соединяющей тела, и является силой притяжения.
Формулу (4.10) можно написать в виде
 (4.11)
(4.11)
В этой формуле  – вектор, проведенный от первого тела ко второму. Его модуль
– вектор, проведенный от первого тела ко второму. Его модуль  , тогда абсолютная величина силы в формулах (4.10) и (4.11) одинакова. Направление этой силы совпадает с направлением вектора
, тогда абсолютная величина силы в формулах (4.10) и (4.11) одинакова. Направление этой силы совпадает с направлением вектора  , т.е. эта сила направлена по линии, соединяющей тела от второго тела к первому.
, т.е. эта сила направлена по линии, соединяющей тела от второго тела к первому.
Приведенные формулы справедливы как для материальной точки, так и для произвольного тела. В последнем случае расстояние  отсчитывается от центров этих тел.
отсчитывается от центров этих тел.
Величина гравитационной постоянной впервые была измерена Кавендишем в 1798 г. с помощью крутильных весов. Физический смысл её заключается в том, что она равна выраженной в ньютонах силе тяготения между точечными телами массой в 1 кг каждая, находящимися на расстоянии 1 м друг от друга. Значение этой величины очень мало. Поэтому малы и силы тяготения. Чтобы силы тяготения были заметны, необходимо, чтобы хотя бы одно из взаимодействующих тел имело огромную массу. Так, сила тяготения между Землей и Луной имеет порядок  Н, а между двумя почти соприкасающимися молекулами кислорода –
Н, а между двумя почти соприкасающимися молекулами кислорода –  Н.
Н.
Данный закон доказывает, что взаимодействие между телами осуществляется через особый вид материи – посредством гравитационного поля.
Отличительным свойством гравитационных сил является то, что они сообщают всем телам, независимо от их массы, одинаковое ускорение. Действительно, если применить формулу для случая взаимодействия земного шара с телами, расположенными вблизи земной поверхности, то выражение силы тяготения тел к Земле можно представить в виде  , где
, где  – масса Земли, R – её радиус,
– масса Земли, R – её радиус,  – масса тела.
– масса тела.
C другой стороны,  , где
, где  – ускорение свободного падения тел вблизи земной поверхности. Сравнивая последние формулы, получим
– ускорение свободного падения тел вблизи земной поверхности. Сравнивая последние формулы, получим 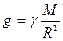 .
.
Так как значения постоянных, входящих в последнюю формулу, известны, ясно, что все тела вблизи поверхности Земли падают с одинаковым ускорением, равным  . Строго говоря, это ускорение зависит от широты и высоты места.
. Строго говоря, это ускорение зависит от широты и высоты места.
Следует отметить ещё одну особенность – особенность массы. Согласно закону всемирного тяготения масса имеет смысл меры силы тяготения (гравитационная масса). Ранее мы говорили, что масса – это мера инертности (инертная масса). Хотя по физическому смыслу эти массы различаются, опыт показывает, что численные значения их отличаются незначительно.
9. Сила тяжести и вес. Невесомость
Вблизи поверхности Земли все тела падают с одинаковым ускорением. Отсюда вытекает, что в системе отсчета, связанной с Землей, на всякое тело действует сила
 (4.12)
(4.12)
Эта сила называется силой тяжести. Она приближенно равна силе гравитационного притяжения тела к Земле. Это различие не превышает 0,36 % и оно связано тем, что система отсчета, связанная с Землей, не вполне инерциальна.
Если подвесить тело или положить его на опору, оно будет покоиться относительно Земли (Рис. 4.2). В этом случае сила тяжести уравновешивается силой  , которую называют реакцией подвеса или опоры. Реакциями называются силы, с которыми на данное тело действуют тела, ограничивающие его движение. По третьему закону Ньютона тело действует на подвес или опору с силой
, которую называют реакцией подвеса или опоры. Реакциями называются силы, с которыми на данное тело действуют тела, ограничивающие его движение. По третьему закону Ньютона тело действует на подвес или опору с силой  , которую называют весом тела.
, которую называют весом тела.

а) б)
Рис. 4.2.
Таким образом,вес тела – это сила, с которой тело действует на подвес или опору вследствие гравитационного притяжения к Земле.
Поскольку силы и
и  уравновешивают друг друга, выполняется условие
уравновешивают друг друга, выполняется условие  .
.
Вес  есть сила, с которой тело действует на подвес (или опору), а
есть сила, с которой тело действует на подвес (или опору), а  есть сила, с которой повес (или опора) действует на тело. Согласно третьему закону Ньютона должно выполняться соотношение
есть сила, с которой повес (или опора) действует на тело. Согласно третьему закону Ньютона должно выполняться соотношение 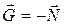 .
.
Сравнение обоих соотношений дает, что
 (4.13)
(4.13)
Таким образом, вес и сила тяжести равны друг другу. Однако приложены они к разным телам – вес к подвесу (или опоре), сила тяжести – к самому телу.
Равенство (4.13) имеет место только в том случае, когда подвес или опора (а, следовательно, и тело) покоится относительно Земли (или движется без ускорения). Если же точка крепления подвеса или опора движется с ускорением, вес перестает быть равным силе тяжести.
                 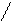   
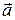
 Рис.4.3. Определение веса тела.
Рис.4.3. Определение веса тела.
| Для пояснения сказанного полезно рассмотреть показания весов, на которых стоит гиря. В неподвижном состоянии на гирю действуют две силы – сила тяжести и сила реакции опоры (весов), причем . Если весы движутся вниз с ускорением а (см. рис.4.3),то уравнение второго закона Ньютона, записанное в неподвижной системе координат[1], имеет вид: . Если весы движутся вниз с ускорением а (см. рис.4.3),то уравнение второго закона Ньютона, записанное в неподвижной системе координат[1], имеет вид:
|
 (4.14)
(4.14)
откуда 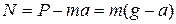 (4.15)
(4.15)
 Учитывая (4.14), вес гири
Учитывая (4.14), вес гири
 (4.16)
(4.16)
Очевидно, что при а = g  , т.е. все свободно падающие тела ничего не весят, т.е. наступает состояние невесомости. Космический корабль, летящий на околоземной орбите с неработающими двигателями, движется, как и оборвавшийся лифт, с ускорением
, т.е. все свободно падающие тела ничего не весят, т.е. наступает состояние невесомости. Космический корабль, летящий на околоземной орбите с неработающими двигателями, движется, как и оборвавшийся лифт, с ускорением  . Поэтому тела внутри корабля находятся в состоянии невесомости – они не оказывают давления на соприкасающиеся с ними тела. В частности, внутренние органы космонавта перестают оказывать давление на органы, расположенные ниже, а вес тела в целом перестает давить на кости скелета. Этим обуславливается специфическое физиологическое ощущение невесомости.
. Поэтому тела внутри корабля находятся в состоянии невесомости – они не оказывают давления на соприкасающиеся с ними тела. В частности, внутренние органы космонавта перестают оказывать давление на органы, расположенные ниже, а вес тела в целом перестает давить на кости скелета. Этим обуславливается специфическое физиологическое ощущение невесомости.
Сила тяжести на поверхности Земли не является постоянной по двум причинам: во-первых, Земля, как известно, не является идеальным шаром (она сплюснута на полюсах так, что на полюсах g больше, чем на экваторе); во-вторых, вследствие суточного вращения Земли, на все тела на ее поверхности (за исключением географических полюсов) действует центростремительное ускорение aц =  соsq, направленное в ту же сторону, что и g. Поэтому вес тел будет меньше там, где радиус вращения больше, т.е. на экваторе тела имеют наименьший вес.
соsq, направленное в ту же сторону, что и g. Поэтому вес тел будет меньше там, где радиус вращения больше, т.е. на экваторе тела имеют наименьший вес.
         r
r
 q
R q
R
| Рис.4.4. Изменение радиуса вращения. |
10. Силы трения
Сила, препятствующая скольжению соприкасающихся тел относительно друг друга, называется силой трения.Силы трения являются проявлением электромагнитных взаимодействий между частицами, входящими в состав молекул.
Так как силы трения зависят от большого числа причин, виды сил трения также разнообразны.
В случае неподвижных относительно друг друга тел существует трение покоя. Максимальная сила трения покоя равна по величине той наименьшей внешней силе, которая вызывает скольжение тел. Она действует между соприкасающимися телами вдоль поверхности их соприкосновения, когда эти тела находятся в покое относительно друг друга. Опыт показывает, что она пропорциональна силе N нормального давления (закон Амонтона-Кулона):
 <
< , (4.17)
, (4.17)
где  – коэффициент трения покоя. Он зависит от свойств поверхностей, между которыми происходит трение, в частности, от веществ, из которых изготовлены трущиеся тела, шероховатости поверхностей, наличия различного рода загрязнений на них, от внешних условий (температуры, влажности и т.д.).
– коэффициент трения покоя. Он зависит от свойств поверхностей, между которыми происходит трение, в частности, от веществ, из которых изготовлены трущиеся тела, шероховатости поверхностей, наличия различного рода загрязнений на них, от внешних условий (температуры, влажности и т.д.).
Если твердое тело скользит по поверхности другого тела, то на него вдоль поверхности соприкосновения тел в сторону, противоположную направлению движения, действует сила, которая называется силой трения скольжения.
Свойства этой силы заключаются в следующем.
1. Из определения следует, что она направлена по касательной к поверхности соприкосновения тел противоположно скорости скольжения данного тела.
2. В отличие от силы трения покоя, она зависит от относительной скорости соприкасающихся при движении тел. В момент начала движения, когда скорость тела ещё мала, сила трения скольжения равна максимальной силе трения покоя  . С увеличением скорости тела она обычно несколько убывает. Например, сдвинуть с места тяжелое тело всегда трудно. Но двигать его после того, как оно уже начало двигаться, заметно легче. При дальнейшем увеличении скорости сила трения скольжения может возрастать.
. С увеличением скорости тела она обычно несколько убывает. Например, сдвинуть с места тяжелое тело всегда трудно. Но двигать его после того, как оно уже начало двигаться, заметно легче. При дальнейшем увеличении скорости сила трения скольжения может возрастать.
3. Если относительная скорость движения тел невелика, величина силы трения покоя определяется по формуле
 (4.18)
(4.18)
В формулы (4.17) и (4.18) входит коэффициент трения. В силу причин, от которых зависят силы трения покоя и скольжения, коэффициент трения является грубой характеристикой сил трения. В физических таблицах обычно приводятся средние значения коэффициента трения. Для точных расчетов необходимо провести экспериментальные исследования в реальных условиях и определить коэффициент трения с использованием формулы (4.18).
Силы трения играют как положительную, так и отрицательную роль.
Благодаря трению приходит в движение и останавливается транспорт. Действие органов передвижения и хватательных органов живых существ основано на трении скольжения. Трение удерживает корни растений в почве, песок – в железнодорожной насыпи и др. Ленточный сепаратор, применяемый для разделения семян на составные части, основан на применении силы трения. Например, смесь зерен овса и проса медленно высыпается из бункера на движущуюся бесконечную ленту, расположенную под углом к горизонту. Угол наклона подбирается так, чтобы зерна овса удерживались на ней силой трения и увлекались вверх, а зерна проса, у которых коэффициент трения с материалом ленты меньше, чем у зерен овса, скользили по ленте вниз. В результате зерна овса и проса будут сыпаться с различных сторон сепаратора.
Силы трения играют отрицательную роль при движении твердых тел в жидкости или газе, или при вращении одного твердого тела внутри другого твердого тела.
Способы уменьшения сил трения.
1. Максимальная величина силы трения покоя заметно уменьшается или может совсем исчезнуть при наличии между поверхностями трущихся тел тонкого слоя вязкой жидкости (смазки). Сила, действующая на твердое тело, движущееся в жидкой среде, со стороны прилегающих к телу слоев жидкости вдоль поверхности тела, называется силой жидкого трения.Опыт показывает, что эта сила зависит от скорости тела  относительно среды. При малых скоростях она пропорциональна скорости и выражается формулой
относительно среды. При малых скоростях она пропорциональна скорости и выражается формулой
 , (4.19)
, (4.19)
а по мере возрастания скорости сила жидкого трения растет пропорционально квадрату скорости:
 (4.20)
(4.20)
Коэффициенты  и
и  называются коэффициентами трения (или сопротивления). Они зависят от:
называются коэффициентами трения (или сопротивления). Они зависят от:
- свойств жидкости, в частности, вязкости и плотности; их величина возрастает с увеличением вязкости;
- формы и размеров тела; если тела имеют одинаковую геометрическую форму, они возрастают с увеличением наибольшей площади сечения тела в направлении, перпендикулярной скорости, и уменьшаются для тел с одинаковым сечением при приближении их формы к обтекаемой ”каплеобразной’’ форме.
2. Замена скольжения качением: применение колес, катков, шариковых и роликовых подшипников. Возникающая при этом сила трения называется силой трения качения.Она выражается формулой:
 , (4.21)
, (4.21)
где R – радиус катящегося тела,  – коэффициент трения качения, зависящий от свойств материала соприкасающихся поверхностей и имеющая размерность длины; N – сила нормального давления (как и в предыдущих случаях).
– коэффициент трения качения, зависящий от свойств материала соприкасающихся поверхностей и имеющая размерность длины; N – сила нормального давления (как и в предыдущих случаях).
Семена некоторых растений (горох, каштан, орех) имеют шарообразную форму, поэтому они проявляют силы трения качения при откатывании на более далекие расстояния от материнского растения.
Контрольные вопросы
1. Какая система отсчета называется инерциальной? Почему система отсчета, связанная с Землей, строго говоря, неинерциальна?
2. В чем заключается физический смысл массы? Назовите её свойства.
3. Что такое сила? Как её можно охарактеризовать?
4. Является ли первый закон Ньютона следствием второго закона Ньютона? Почему?
5. Сформулировав три закона Ньютона, покажите, какова взаимосвязь между этими законами?
6. В чем заключается принцип независимости действия сил?
7. Назовите и охарактеризуйте виды взаимодействий.
8. Назовите особенности гравитационных сил?
9. Какова физическая сущность трения? В чем отличие сухого трения от жидкого?
10. Что называется механической системой? Какие системы называются замкнутыми? Является ли Вселенная замкнутой системой? Почему?
11. В чем заключается закон сохранения импульса? В каких системах он выполняется? Почему он является фундаментальным законом природы?
12. В чем измеряется коэффициент трения качения?
13. Какова роль силы трения в природе и технике? Ответ обоснуйте конкретными примерами.
14. В чем роль силы трения при качении тел?
15. Почему пассажиры любого вида транспорта при внезапной остановке наклоняются вперед, а при резком увеличении скорости движения – назад?
16. При каком условии пароход, плывущий против течения, будет иметь постоянную скорость?
17. Почему при выстреле пуля оставляет в стекле небольшое отверстие, а брошенная рукой – разбивает стекло на кусочки?
18. Канат переброшен через блок, причем часть каната лежит на столе, часть – на полу. После того как канат отпустили, он начал двигаться со временем равномерно. Определите скорость этого движения, если высота стола h.
19. Если концы деревянной палки положить на два стакана и с силой ударить палку тяжелым предметом посередине, палка переломится, а стаканы останутся целы. Как можно объяснить это явление?
20. Тело движется по горизонтальной поверхности. Форма траектории – окружность. Как будет изменяться вектор силы трения при движении?
21. Всегда ли трение скольжения больше трения качения?
22. Диаметр одного шарика в два раза больше, чем другого. После начального периода ускоренного движения шарики равномерно падают в воздухе. Плотность их одинакова. Сила сопротивления воздуха пропорциональна квадрату скорости и площади поперечного сечения шарика (площадь большого круга). Определите, во сколько раз различаются скорости падения шариков. Выталкивающей силой, действующей в воздухе на шарики, пренебречь.
23. На гладкую доску положили два кирпича, один плашмя, другой – на ребро. Вес кирпичей одинаков. Какой кирпич начнет сползать первым, если постепенно поднимать один конец доски?
24. Можно ли уничтожить трение между двумя поверхностями, тщательно их отшлифовав?
25. На спускающегося парашютиста действует сила земного притяжения, но движется он равномерно. Объясните это.
26. Масса одного тела меньше другого. Если бы Земля притягивала все тела с одинаковой силой, какое тело упало бы быстрее? Первоначально они находились на одинаковой высоте.
27. Шарику, который первоначально находился на горизонтальном столе высотой h, сообщили скорость v0, и он скатился по желобу на землю. Какую форму должен иметь желоб, чтобы при скатывании шарик все время касался желоба, не оказывая на него давления?
28. Какие часы целесообразно применять во время космических полетов: гиревые с маятником или пружинные? Как определить массу тела в мире невесомости?
29. Покажите, что второй закон Ньютона для тел, между которыми действуют гравитационные силы, не меняются при переходе от одной инерциальной системы отсчета к другой, движущейся со скоростью  относительно первой.
относительно первой.
30. Зачем в вертолетах, кроме основного винта – ротора, создающего силу, направленную вверх, устанавливают на хвостовой балке небольшой винт, создающий тягу в направлении, приблизительно перпендикулярном к направлению полета?
31. Что является более прочным для удержания одного и того же веса – гамак или качели, находящиеся в покое?
32. Альпинисты переправляются через глубокий овраг, держась руками на натянутую над ними веревку. Что целесообразнее для безопасности – туго натянуть канат или ослабить его? В каком случае канат может скорее оборваться?
33. Как с помощью небольшой силы, имея трос, вытащить загрузший автомобиль?
34. В зависимости от угла наклона тело, находящееся на наклонной плоскости, может оставаться в покое, двигаться по ней равномерно или равноускоренно. Каково соотношение между действующими на тело силами во всех трех случаях?
35. Шнуром, перекинутым через блок, равномерно поднимают груз, натягивая конец шнура горизонтально. Чему равна сила давления на блок? Будет ли она больше (меньше) веса груза или равна ему?
36. Одно и то же тело взвесили на пружинных весах на экваторе и полюсе. Каковы показания приборов?
37. Почему скорость поезда на горизонтальном участке пути не возрастает бесконечно, если сила тяги двигателя действует непрерывно?
38. Тела падают вследствие притяжения Земли. В чем неточность этого выражения?
39. Как объяснить, что бегущий человек, споткнувшись, падает в направлении своего движения, а, поскользнувшись, падает в направлении, противоположном направлению своего движения?
40. Докажите свойство аддитивности массы. Верно ли утверждение о том, что аддитивность и закон сохранения массы вещества – одинаковые понятия?
Лекция №5. Динамика системы материальных точек
1. Центр масс системы материальных точек
На практике не каждое тело может быть представлено как материальная точка. Однако всегда можно ее разделить на достаточно малые части, каждую из которых можно считать материальной точкой.
Ещё чаще приходится иметь дело не с одним-двумя телами, а с системой тел, взаимодействующих между собой. Изучение движения такой системы – весьма сложная задача, так как в общем случае для описания движения системы нужно знать движение всех её частей. Такое изучение облегчается тем, что у самых различных систем имеются общие свойства. В частности, таким общим свойством является то, что в любой системе можно выделить особую по отношению ко всем другим точкам системы точку, которая называется центром масс системы.
Рассмотрим две материальные точки А и В с массами  и
и  , расположенные в плоскости хОу.
, расположенные в плоскости хОу.
 Рис. 5.1
Рис. 5.1
| Центром масс двух материальных точек А и В с массами  и и  соответственно называется точка С, лежащая на отрезке, соединяющем А и В, на расстояниях соответственно называется точка С, лежащая на отрезке, соединяющем А и В, на расстояниях  и и 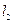 от А и В, (рис.5.1) обратно пропорциональных массам точек, т.е. от А и В, (рис.5.1) обратно пропорциональных массам точек, т.е.
 (5.1) (5.1)
|
При этом центр масс необязательно совпадает с какой-либо материальной точкой системы.
Если положения точек А и В задаются радиусами-векторами  и
и  , то положение центра масс определяется радиусом-вектором
, то положение центра масс определяется радиусом-вектором 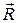 . Соединим массы
. Соединим массы  и
и  с центром массточек отрезками
с центром массточек отрезками  и
и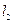 , направленными от точек А и В к центрумасс, как показано на рисунке. Тогда
, направленными от точек А и В к центрумасс, как показано на рисунке. Тогда
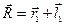 и
и 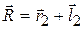 (5.2)
(5.2)
Умножим первое уравнение на  , а второе на
, а второе на  :
:
 и
и 
и сложим их:  (5.3)
(5.3)
Но с учетом определения (5.1) и направлений векторов  и
и 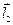 имеем, что
имеем, что 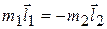 . Тогда из (5.3) получим соотношение:
. Тогда из (5.3) получим соотношение:
 (5.4)
(5.4)
или  (5.5)
(5.5)
Формулы (5.4) и (5.5) могут быть обобщены на любое количество материальных точек. При этом радиус-вектор центра масс 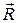 системы, состоящей из n материальных точек, определяется формулой
системы, состоящей из n материальных точек, определяется формулой
 (5.6)
(5.6)
Здесь  – масса точки с номером i,
– масса точки с номером i,  – её радиус-вектор, а
– её радиус-вектор, а  – полная масса системы точек.
– полная масса системы точек.
Из формулы (5.6) следуют формулы для вычисления координат центра масс через координаты и массы точек системы:
 ,
,  ,
,  (5.7)
(5.7)
Скорость центра масс системы материальных точек также выражается через массы и скорости отдельных материальных точек системы. Действительно, в силу определения скорости запишем выражение для скорости центра масс в виде:
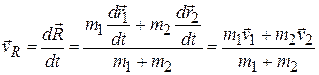 (5.8)
(5.8)
или
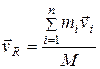 (5.9)
(5.9)
Так же может быть найдено и выражение для ускорения центра масс системы:  , т.е.
, т.е. (5.10)
(5.10)
Величины  представляют собой импульсы отдельных точек, поэтому уравнение (5.9) можно переписать в виде:
представляют собой импульсы отдельных точек, поэтому уравнение (5.9) можно переписать в виде:
 , (5.11)
, (5.11)
где 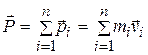 – импульс системы материальных точек. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость её центра масс.
– импульс системы материальных точек. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость её центра масс.
Дифференцируя (5.11), находим уравнение движения системы материальных точек в следующем виде:
 (5.12)
(5.12)
Отсюда следует, что центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы.
2. Закон сохранения импульса
Совокупность тел, выделенных для рассмотрения, называется механической системой. Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соответствии с этим силы, действующие на тела системы, подразделяются на внутренние и внешние. Внутренними называют силы, с которыми тела системы действуют друг на друга,а внешними – силы, действующие со стороны тел, не принадлежащих системе.Обозначим внутренние силы через  , где первый индекс указывает номер частицы, на которую действует сила, второй индекс – номер частицы, воздействием которой обусловлена эта сила. Символом
, где первый индекс указывает номер частицы, на которую действует сила, второй индекс – номер частицы, воздействием которой обусловлена эта сила. Символом 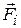 обозначим результирующую всех внешних сил, действующих на i-ую частицу. Согласно третьему закону Ньютона
обозначим результирующую всех внешних сил, действующих на i-ую частицу. Согласно третьему закону Ньютона  , т.е.
, т.е.  . Отсюда следует, что геометрическая сумма всех внутренних сил, действующих в системе, равна нулю.
. Отсюда следует, что геометрическая сумма всех внутренних сил, действующих в системе, равна нулю.
Рассмотрим движение механической системы, состоящей из двух материальных точек. Обозначим внутренние силы: через 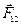 – силу, действующую на первую точку со стороны второй, и
– силу, действующую на первую точку со стороны второй, и 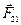 – силу, действующую на вторую точку со стороны первой. Сумму внешних сил, действующих на первую и вторую точки, обозначим через
– силу, действующую на вторую точку со стороны первой. Сумму внешних сил, действующих на первую и вторую точки, обозначим через  и
и 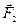 соответственно.
соответственно.
Движение каждой точки описывается вторым законом Ньютона:
 ,
,  , (5.13)
, (5.13)
где  – импульсы точек с массами
– импульсы точек с массами 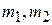 . Сложив эти два уравнения, получим:
. Сложив эти два уравнения, получим:
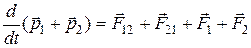 (5.14)
(5.14)
Согласно третьему закону Ньютона, внутренние силы попарно равны и противоположны, т.е.  . Поэтому в формуле (5.14) сумма внутренних сил обращается в нуль. С другой стороны, по определению
. Поэтому в формуле (5.14) сумма внутренних сил обращается в нуль. С другой стороны, по определению 
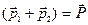 – импульс системы. Таким образом,
– импульс системы. Таким образом,
 (5.15)
(5.15)
Легко видеть, что в случае произвольного числа n материальных точек в левой части всегда будет производная полного импульса системы, а в правой части – сумма всех внешних сил. Поэтому в общем случае имеем
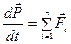 , (5.16)
, (5.16)
т.е. производная по времени импульса системы материальных точек равна сумме всех внешних сил, действующих на точки системы. Уравнение (5.16) называют законом изменения импульса системы материальных точек или теоремой о движении центра масс.
Согласно этой теореме центр масс движется как материальная точка, на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Примером может служить движение снаряда по параболе в безвоздушном пространстве. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки под действием внутренних сил будут разлетаться в разные стороны.Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было.
Как видно из уравнения (5.16), изменение суммарного импульса определяется равнодействующей всех внешних сил, действующих на систему. В связи с этим рассмотрим ряд важных следствий, вытекающих из уравнения (5.16).
1. Рассмотрим систему материальных точек, которая не подвергается воздействию внешних сил.Такая система называется замкнутой.В этом случае правая часть уравнения (5.16) в любой момент времени равна нулю. Тогда
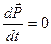 (5.17)
(5.17)
Это значит, что  (5.18)
(5.18)
Уравнение (5.18) называется законом сохранения импульса: полный импульс всех тел замкнутой системы сохраняется во времени.
Можно также показать, что при выполнении условия (5.17) центр масс замкнутой системы движется равномерно и прямолинейно.
2.Внешние силы на точки системы действуют, но их сумма равна нулю. В этом случае также выполняется закон сохранения импульса. Например, если тела движутся по гладкой горизонтальной поверхности, то силы тяжести и силы реакции со стороны поверхности, действующие на эти тела и являющиеся внешними, все время равны и противоположны.
3.Так как уравнение (5.18) векторное, то оно выполняется также для проекций на любое направление. Поэтому, если сумма проекций внешних сил на какое-то направление в любой момент времени равна нулю, то проекция импульса системы на это направление остается постоянной, хотя проекции импульса на другие направления могут при этом изменяться.
Примерами действия закона сохранения импульса могут служить отдача при стрельбе из огнестрельного оружия, реактивное движение, перемещение осьминогов и т.п.
Закон сохранения импульса справедлив не только в классической механике, хотя он получен как следствие законов Ньютона. Эксперименты показывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т.е. закон сохранения импульса – фундаментальный закон природы.
В природе реактивное движение используется некоторыми живыми организмами. Например, кальмары, спруты, медузы и некоторые двухстворчатые моллюски передвигаются посредством отдачи воды, выбрасываемой ими из особых полостей тела. При этом кальмары развивают большую скорость движения – 70 км/час.
Своеобразным примером реактивного движения является «бешеный огурец» – растение южного Крыма. Внутри созревшего плода этого растения находится жидкость под повышенным давлением. Оторванный от стебля «бешеный огурец» вырывается из рук и отлетает в сторону за счет отдачи струи жидкости, выбрасываемой из отверстия, образующегося в месте крепления к плодоножке.
3. Движение тел с переменной массой. Реактивное движение
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты заключается в следующем. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с огромной силой. Выбрасываемое вещество той же силой, но противоположно направленной, в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
Пусть  – масса ракеты в произвольный момент времени
– масса ракеты в произвольный момент времени  , а
, а  – ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет
– ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет  . Спустя время
. Спустя время 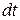 масса и скорость ракеты получат приращения. Заметим, что величина
масса и скорость ракеты получат приращения. Заметим, что величина  отрицательна. Количество движения ракеты станет равным
отрицательна. Количество движения ракеты станет равным 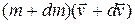 .
.
Обозначим через 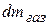 массу газов, образовавшихся за время
массу газов, образовавшихся за время 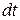 , а через
, а через  – их скорость. Тогда количество движения газов, образовавшихся за время
– их скорость. Тогда количество движения газов, образовавшихся за время 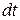 равно
равно 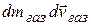 . Из современной формулировки второго закона Ньютона имеем, что
. Из современной формулировки второго закона Ньютона имеем, что
 ,
,
где  – геометрическая сумма всех внешних сил, действующих на ракету.
– геометрическая сумма всех внешних сил, действующих на ракету.
Таким образом,
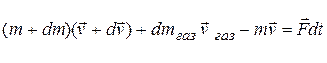 (5.19)
(5.19)
Раскрывая скобки и учитывая, что  и
и  – малые величины за время
– малые величины за время 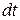 , можно отбросить произведение
, можно отбросить произведение 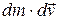 как бесконечно малую высшего порядка. Обозначим через
как бесконечно малую высшего порядка. Обозначим через  скорость истечения газов относительно ракеты, которую называют скоростью газовой струи ракеты.Кроме того, из закона сохранения массы следует, что
скорость истечения газов относительно ракеты, которую называют скоростью газовой струи ракеты.Кроме того, из закона сохранения массы следует, что
 .
.
С учетом этих замечаний выражение (5.19) преобразуется к виду
 . (5.20)
. (5.20)
Разделим это выражение на 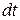 и из (5.20) получим
и из (5.20) получим
 (5.21)
(5.21)
По форме уравнение (5.21) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела 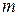 здесь не постоянна, а меняется во времени из-за потери вещества. Кроме того, в правой части выражение
здесь не постоянна, а меняется во времени из-за потери вещества. Кроме того, в правой части выражение  имеет смысл дополнительной внешней силы. Она называется реактивной силойи имеет значение силы, с которой действуют на ракету вытекающие из нее газы. Уравнение (5.21) впервые было получено русским механиком И.В.Мещерским и называется уравнением Мещерского или уравнением движения точки с переменной массой.
имеет смысл дополнительной внешней силы. Она называется реактивной силойи имеет значение силы, с которой действуют на ракету вытекающие из нее газы. Уравнение (5.21) впервые было получено русским механиком И.В.Мещерским и называется уравнением Мещерского или уравнением движения точки с переменной массой.
Применим уравнение(5.21) к движению ракеты, на которую не действуют никакие внешние силы. Полагая  , получим
, получим
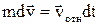 (5.22)
(5.22)
Предположим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи  . За положительное направление примем направление полета. Тогда в скалярной форме уравнение (5.22) примет вид
. За положительное направление примем направление полета. Тогда в скалярной форме уравнение (5.22) примет вид
 .
.
Следовательно,
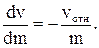 (5.23)
(5.23)
Скорость газовой струи может меняться во время полета. Однако для простоты мы примем, что она постоянна. В этом случае

Значение постоянной интегрирования С определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна  . Тогда предыдущее уравнение дает
. Тогда предыдущее уравнение дает
 откуда
откуда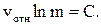
Следовательно,
 (5.24)
(5.24)
или (5.25)
(5.25)
Формула (5.25) называется формулой Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый для сообщения ракете определенной скорости. Она показывает, что:
- чем больше конечная масса ракеты, тем больше должна быть ее стартовая скорость;
- чем больше скорость истечения газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнение Мещерского и формула Циолковского получены для нерелятивистских движений, т.е. для случаев, когда скорости  и
и 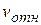 малы по сравнению со скоростью света.
малы по сравнению со скоростью света.
4. Задача двух тел. Приведенная масса
Рассмотрим замкнутую систему, состоящую из двух взаимодействующих материальных точек с массами  и
и  (рис.5.2). Уравнения движения этих точек можно записать в виде
(рис.5.2). Уравнения движения этих точек можно записать в виде
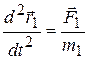 ,
, (5.30)
(5.30)
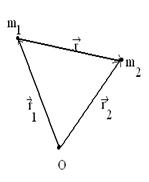
| Рис. 5.2. |
По третьему закону Ньютона  .
.
Вычитая из одного уравнения другое, находим

Это уравнение описывает движение одной материальной точки относительно другой, так как разность  есть радиус-вектор, проведенный от первой точки ко второй. Он однозначно определяет положение второй точки относительно первой. Введем обозначение
есть радиус-вектор, проведенный от первой точки ко второй. Он однозначно определяет положение второй точки относительно первой. Введем обозначение
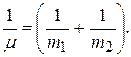 или
или  , (5.31)
, (5.31)
которое называется приведенной массой.
Тогда предыдущее уравнение перейдет к виду
 , (5.32)
, (5.32)
что формально аналогично второму уравнению Ньютона.
Понятие приведенной массы глубокого физического смысла не имеет. Введение этого понятия позволяет определить относительное движение одной материальной точки относительно другой в ее силовом поле.
Контрольные вопросы
1. Что называется центром масс системы материальных точек?
2. Что называется механической системой?
3. Какие системы называются замкнутыми?
4. Является ли Вселенная замкнутой системой? Почему?
5. В чем заключается закон сохранения импульса? В каких системах он выполняется? Почему он является фундаментальным законом природы?
6. Обобщите закон сохранения импульса для случая релятивистских движений.
7. В чем заключается постоянство скорости центра масс замкнутой системы?
8. На тележке стоят два бака, соединенные между собой в нижней части трубкой с краном. Один из баков наполнен водой. При открывании крана вода переливается в пустой бак. Будет ли при этом двигаться тележка? Когда она остановится? Трение между тележкой и землей не учитывать.
9. Зенитный снаряд разрывается на высоте h от земли на большое число осколков, имеющих одинаковую начальную скорость 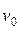 и равные массы. Найдите расстояние между двумя осколками, лежащими на прямой, проходящей через центр инерции всей системы и образующей угол
и равные массы. Найдите расстояние между двумя осколками, лежащими на прямой, проходящей через центр инерции всей системы и образующей угол  с вертикалью, через время
с вертикалью, через время  после разрыва.
после разрыва.
10. Почему удар молотком по тяжелой наковальне, положенной на грудь циркового артиста, оказывается для него безвредным, тогда как такой же удар прямо по телу артиста является гибельным?
11. Приведите примеры проявления закона сохранения импульса.
12. Что такое приведенная масса и в чем смысл введения этого понятия?
Лекция №6. Законы сохранения
Для замкнутой системы тел остаются постоянными три физические величины: энергия, импульс и момент импульса. Соответственно имеются три закона сохранения: закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса. Второй закон – закон сохранения импульса изучили в предыдущем разделе. Настоящий раздел посвящен рассмотрению остальных двух законов сохранения в механике.
1. Работа
Понятия работы и энергии широко используются в нашей повседневной жизни. Эти понятия тесно связаны друг с другом. Например, говорят об энергичном или работоспособном человеке, или говорят, что «очень устал, очень много работал или энергию затратил и т.д.». Греческое слово «энергия» означает «деятельность». Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Например, совершая работу при заводе часов, мы создаем запас энергии в пружине, за счет которого затем идут часы.
Пусть при перемещении материальной точки В по некоторой траектории на малый отрезок  на эту точку действует сила
на эту точку действует сила  , направление которой составляет угол
, направление которой составляет угол  с направлением перемещения (рис.6.1).
с направлением перемещения (рис.6.1).

| Рис.6.1 |
Элементарной работой  силы
силы  на малом перемещении
на малом перемещении  называется произведение величины
называется произведение величины  этой силы на величину
этой силы на величину 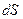 перемещения и на косинус угла
перемещения и на косинус угла  между направлением силы и направлением перемещения:
между направлением силы и направлением перемещения:
 (6.1)
(6.1)
Из определения (6.1) следуют следующие особенности элементарной работы.
1. Элементарная работа – это скалярное произведение силы на малое перемещение, т.е.
 (6.2)
(6.2)
Она может быть представлена в виде
 , (6.3)
, (6.3)
или  , (6.4)
, (6.4)
где  – проекция силы на направление перемещения,
– проекция силы на направление перемещения, 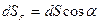 – проекция перемещения на направление силы.
– проекция перемещения на направление силы.
Последние формулы показывают, что перемещение тела обусловлено только касательной составляющей силы  , которую называют движущей силой. Причем, эта сила должна быть постоянной на элементарном перемещении
, которую называют движущей силой. Причем, эта сила должна быть постоянной на элементарном перемещении  . Поэтому элементарная работа равна произведению постоянной движущей силы на величину перемещения.
. Поэтому элементарная работа равна произведению постоянной движущей силы на величину перемещения.
2. Работа – скалярная величина. Она может быть как положительной, так и отрицательной. При 0< <90° работа положительна – сила вызывает перемещение тела; при 90°<
<90° работа положительна – сила вызывает перемещение тела; при 90°< <180° работа отрицательна – сила препятствует движению тела; при
<180° работа отрицательна – сила препятствует движению тела; при  =90° сила не совершает работы по перемещению тела. Если направления силы и перемещения совпадают (
=90° сила не совершает работы по перемещению тела. Если направления силы и перемещения совпадают ( = 0°), то
= 0°), то
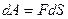 (6.5)
(6.5)
3. Если материальная точка перемещается под действием нескольких сил, то совершаемая ими работа равна сумме работ всех этих сил.
4. Если работа совершается переменной силой, то следует разделить участок траектории на элементарные отрезки так, чтобы их можно было считать прямолинейным, и сложить элементарные работы, совершаемые движущей силой на каждом из отрезков этого участка:
 , (6.6)
, (6.6)
где аb – участок траектории.
Из формулы (6.6) вытекает, что полная работа, совершаемая материальной точкой под действием постоянной движущей силы по всей траектории, равна:
 (6.7)
(6.7)
5.Работа является количественным выражением действия силы или взаимодействия тел. Поэтому конечное выражение для вычисления работы определяется видом взаимодействия. Например, если на тело действует только сила тяжести, работа, совершаемая телом, равна: 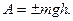 Если тело поднимается вверх, то сила тяжести совершает отрицательную работу, если оно опускается вниз, то – положительную работу. Величина работы не зависит от формы траектории, по которой двигалось тело, а определяется лишь тем, насколько выше или ниже находится конечная точка участка траектории по сравнению с начальной.
Если тело поднимается вверх, то сила тяжести совершает отрицательную работу, если оно опускается вниз, то – положительную работу. Величина работы не зависит от формы траектории, по которой двигалось тело, а определяется лишь тем, насколько выше или ниже находится конечная точка участка траектории по сравнению с начальной.
Силы, работа которых не зависит от формы и длины пути (траектории), а зависит лишь от начального и конечного положения тела, на которое они действуют, называются консервативными. Из этого определения следует, что работа по любому замкнутому контуру для таких сил равна нулю:
 =0 (6.8)
=0 (6.8)
К ним относятся все центральные силы, т.е. силы всемирного тяготения (и силы тяжести), силы упругости и др. К неконсервативным силам относятся, например, сила трения скольжения, силы сопротивления движению тел.
Силы трения называют также диссипативными силами, поскольку при наличии в системе материальных точек взаимодействий, осуществляемых этими силами, происходит исчезновение механической энергии и превращение её в тепловую (диссипация – рассеяние, уничтожение).
6.В качестве единицы работы в СИ является джоуль (Дж), который равен работе, совершаемой силой 1 Н на пути 1 м; в СГС-системе – эрг, равный работе, совершаемой силой 1 дин на пути 1 см.
7.Работа, совершаемая в единицу времени, называется мощностью.
Мощность P определяется соотношением 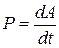 , где
, где 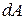 – работа, совершаемая за время
– работа, совершаемая за время 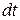 . Подставив вместо
. Подставив вместо 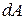 выражение (6.2) и приняв во внимание определение скорости, получим
выражение (6.2) и приняв во внимание определение скорости, получим  .
.
Таким образом, мощность равна скалярному произведению силы на скорость точки приложения силы.
Единицей мощности является такая мощность, при которой за одну секунду совершается работа, равная одному джоулю. Эта единица называется ваттом (Вт).
2. Энергия и работа
Энергиейназывают физическую величину, являющуюся общей количественной мерой различных форм движения и существования материи, происходящих в результате совершения работы.
Таким образом, энергия является функцией состояния тела, например, движение тела приводит к изменению его энергии. Сам процесс изменения есть результат работы:  .
.
Катящийся шар, сталкиваясь с некоторым телом, перемещает его, т.е. совершает работу. Следовательно, катящийся шар обладает энергией. Кроме того, катящийся шар обладает энергией независимо от того, совершает он в данный момент работу или нет: энергия характеризует состояние системы, способность (возможность) системы к совершению работы при переходе из одного состояния в другое.
В физике в соответствии с различными физическими процессами и взаимодействиями различают механическую, тепловую, электромагнитную, ядерную и другие энергии.
Механическая энергия состоит из кинетической и потенциальной энергий.
3. Кинетическая энергия и работа
Пусть под действием некоторой силы  тело (материальная точка) массой
тело (материальная точка) массой  совершает перемещение, изменив скорость от
совершает перемещение, изменив скорость от  до
до  , т.е. движется с ускорением
, т.е. движется с ускорением 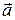 . Напишем уравнение движения тела:
. Напишем уравнение движения тела:
 (6.9)
(6.9)
Учитывая определение ускорения материальной точки и умножив уравнение (6.9) на перемещение точки 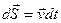 , получим
, получим
 (6.10)
(6.10)
Проинтегрировав соотношение  с учетом изменения скорости тела, имеем
с учетом изменения скорости тела, имеем 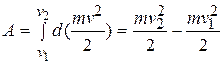 .
.
Введем обозначение  , которое называется кинетической энергией тела.
, которое называется кинетической энергией тела.
Итак, совершенная силой работа равна приращению кинетической энергии тела:
 (6.11)
(6.11)
В этом заключается и физический смысл работы.
Из определения следует, что:
- кинетическая энергия – это энергия движения;
- кинетическая энергия – скалярная величина;
- кинетическая энергия системы материальных точек равна сумме кинетических энергий всех точек, составляющих систему;
- измеряется в тех же единицах, что и работа.
4. Потенциальная энергия
Потенциальная энергия обусловлена характером взаимодействия между телами, их взаимным расположением. Поэтому вид формулы для потенциальной энергии зависит от конкретного вида взаимодействия тел.
Так, например, работа силы тяжести, необходимая для изменения положения тела относительно Земли, равна: 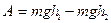 , где
, где  – начальная и конечная высота (
– начальная и конечная высота ( ) тела относительно Земли. Выражение
) тела относительно Земли. Выражение  называется потенциальной энергией силы тяжести. Эта работа равна изменению потенциальной энергии тела:
называется потенциальной энергией силы тяжести. Эта работа равна изменению потенциальной энергии тела:
 (6.12)
(6.12)
Положительная работа сил тяжести соответствует убыли потенциальной энергии. Наоборот, если бы тело поднималось над поверхностью Земли, приращение потенциальной энергии соответствовало бы отрицательной работе. Поэтому в общем случае следует записать:  . Так как
. Так как  , то
, то 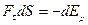 и
и
 (6.13)
(6.13)
Формула (6.13) показывает, что консервативная сила – сила тяжести – равна градиенту потенциальной энергии, взятому с обратным знаком:
 (6.14)
(6.14)
Эта формула связывает между собой силу и соответствующую ей потенциальную энергию, что дает возможность вычислить потенциальную энергию в каждом конкретном случае вида взаимодействия тел.
Пример. Пусть задана сила всемирного тяготения  . Так как
. Так как  , из формулы (6.13) найдем
, из формулы (6.13) найдем
 .
.
Обычно за начальную конфигурацию системы, состоящую из двух материальных точек, взаимодействующих между собой силами всемирного тяготения, принимают расположение этих точек на бесконечно большом расстоянии друг от друга, где  =0. Тогда потенциальная энергия взаимодействия точек равна
=0. Тогда потенциальная энергия взаимодействия точек равна
 (6.15)
(6.15)
Как и закон всемирного тяготения, эта формула верна не только для материальных точек, но и для любых сферически симметричных тел.
Физически знак минус обусловлен тем, что по мере самопроизвольного сближения тяготеющих тел их потенциальная энергия должна уменьшаться, переходя в кинетическую. Из формулы (6.15) следует, что максимальное значение потенциальной энергии тяготеющие тела будут иметь в том случае, когда они бесконечно удалены друг от друга.
Выше мы говорили о потенциальных и консервативных силах. Они тождественны лишь в случае стационарного силового поля, т.е. поля, остающегося постоянным во времени. Поле консервативных сил является частным случаем потенциального силового поля. Для нестационарного силового поля, т.е. поля, изменяющегося во времени, формула (6.14) не выполняется. Поэтому отождествлять потенциальные и консервативные силы нельзя.
5. Закон сохранения и превращения механической энергии
Рассмотрим систему, состоящую из двух материальных точек с массами  . Пусть частицы взаимодействуют друг с другом с силами
. Пусть частицы взаимодействуют друг с другом с силами  , модули которых зависят только от расстояния между материальными точками
, модули которых зависят только от расстояния между материальными точками  . Такие силы являются консервативными. Предположим, что, кроме консервативных сил, на каждую точку действуют внешняя консервативная сила
. Такие силы являются консервативными. Предположим, что, кроме консервативных сил, на каждую точку действуют внешняя консервативная сила  и внешняя неконсервативная сила
и внешняя неконсервативная сила  . Тогда уравнение движения каждой точки имеет вид:
. Тогда уравнение движения каждой точки имеет вид:
 ,
, 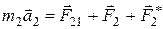 (6.16)
(6.16)
Умножив уравнения (6.16) на соответствующие перемещения 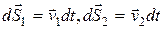 , учитывая определение ускорения материальной точки и сложив вместе полученные уравнения, имеем
, учитывая определение ускорения материальной точки и сложив вместе полученные уравнения, имеем
 (6.17)
(6.17)
Левая часть представляет собой приращение кинетической энергии системы:
 (6.18)
(6.18)
Первый и четвертый члены правой части равны убыли потенциального взаимодействия частиц:  (6.19)
(6.19)
Второй и пятый члены правой части равны убыли потенциальной энергии во внешнем поле консервативных сил: 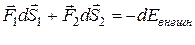 .
.
Остальные члены представляют собой работу неконсервативных внешних сил:
 (6.20)
(6.20)
Приняв во внимание (6.18)-(6.20), представим соотношение (6.17) следующим образом:
 (6.21)
(6.21)
Величина 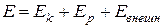 есть полная механическая энергия системы. Если внешние неконсервативные силы отсутствуют, правая часть формулы (6.20) будет равна нулю и, следовательно, полная энергия системы остается постоянной:
есть полная механическая энергия системы. Если внешние неконсервативные силы отсутствуют, правая часть формулы (6.20) будет равна нулю и, следовательно, полная энергия системы остается постоянной:
 (6.22)
(6.22)
Таким образом, мы пришли к выводу, что полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной. В этом и заключается закон сохранения механической энергии.
Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, соотношение (6.22) имеет вид
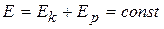 (6.23)
(6.23)
В этом случае закон сохранения механической энергии формулируется следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.
Если в замкнутой системе, кроме консервативных, действуют также неконсервативные силы, например силы трения, то полная механическая энергия системы не сохраняется. Рассматривая неконсервативные силы как внешние, можно в соответствии с (6.21) написать
 (6.24)
(6.24)
Пример. Основными запасниками механической энергии во время бега и других циклических движений являются сухожилия. Каждый из нас может убедиться, что механическая энергия действительно запасается в наших ногах, как в пружинах. Сильно сгибая ноги в этом можно убедиться. Мы сразу заметим, что подниматься гораздо легче, если выпрямить ноги сразу, чем если задерживаться на секунду. Это можно объяснить тем, что при сгибании колен часть мышц напряжена, контролируя движение вниз, и их сухожилия растянуты. Если перед подъемом сухожилиям не дать возможность укоротиться, запасенная в них потенциальная энергия перейдет в кинетическую. В этом случае выполняется закон сохранения механической энергии для замкнутой системы тел. В противном случае между мышцами появляются неконсервативные силы, что проявляется в нагреве тела: полная механическая энергия системы не сохраняется, часть механической энергии переходит в тепловую.
Свойства сухожилий более или менее одинаковы у всех животных. Однако конечности копытных, например, овец и лошадей, наиболее приспособлены для хранения механической энергии. Некоторые мышцы в нижних частях ног этих животных состоят практически целиком из одних сухожилий. Самым выразительным примером такого использования сухожилий могут служить нижние конечности верблюда. В ноге человека самым мощным является ахиллово сухожилие, на которое при беге может действовать растягивающая сила до 4000 Н.
6. Соударение двух тел
Ударом называется кратковременное столкновение соударяющихся тел. Соударяющиеся тела можно считать замкнутой системой, так как возникающие при кратковременном ударе внутренние силы системы во много раз превосходят внешние. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий.
Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает. Кинетическая энергия тел полностью или частично переходит во внутреннюю энергию. После удара столкнувшиеся тела либо покоятся, либо движутся с одинаковой скоростью. При абсолютно неупругом ударе выполняется только закон сохранения импульса.
Пусть массы соударяющихся частиц (материальных частиц) равны  и
и  , а скорости до удара –
, а скорости до удара –  и
и 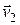 , а после соударения –
, а после соударения –  . По закону сохранения импульса
. По закону сохранения импульса 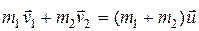 .
.
Отсюда имеем 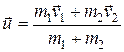 (6.25)
(6.25)
Можно найти изменение кинетической энергии шаров, т.е. ту часть, которая перешла во внутреннюю энергию:
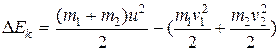 .
.
Подставляя сюда (6.25), получим  . Эта энергия переходит в тепловую энергию.
. Эта энергия переходит в тепловую энергию.
Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, модуль и направление которых определяются двумя условиями – сохранением полной энергии и сохранением полного импульса системы тел.
В качестве примера рассмотрим абсолютно упругий центральный удар двух однородных шаров. Удар называетсяцентральным, если шары до удара движутся вдоль прямой, проходящей через их центры.
Обозначим скорости шаров после удара через 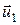 и
и  . Напишем законы сохранения энергии и импульса:
. Напишем законы сохранения энергии и импульса:
 , (6.26)
, (6.26)
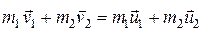 (6.27)
(6.27)
Решая эту систему уравнений, находим скорости шаров после удара:
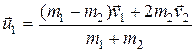 ,
,  (6.28)
(6.28)
Отметим, что скорости шаров после абсолютно упругого удара не могут быть одинаковыми.
7. Момент силы относительно неподвижного центра
Повседневный опыт показывает, что при вращении какого-либо тела с помощью рычага существенным оказывается не только модуль силы, но и длина рычага.Для описания динамики вращения такого тела необходимо ввести понятие момента силы.При этом надо различать понятия момента силыотносительно точки и относительно оси. Это разные понятия.
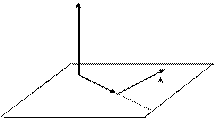  M
O F
r a
A
Рис.6.2. Момент силы относительно точки
M
O F
r a
A
Рис.6.2. Момент силы относительно точки
| Момент силы относительно точки сам есть вектор. Момент того же вектора относительно оси есть проекция на эту ось его момента относительно точки, лежащей на той же оси. Таким образом, момент вектора относительно оси уже не является вектором. Рассмотрим момент силы относительно точки. |
Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы или вектора импульса. Ее называют началом или полюсом. Обозначим радиус-вектор , проведенный из этой точки к точке приложения силы
, проведенный из этой точки к точке приложения силы  (Рис.6.2). Моментом силы
(Рис.6.2). Моментом силы  относительно неподвижной точки О называется векторное произведение радиуса-вектора
относительно неподвижной точки О называется векторное произведение радиуса-вектора  , проведенного из точки О к точке А, и вектора силы
, проведенного из точки О к точке А, и вектора силы 
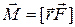 (6.29)
(6.29)
Из этого определения следует, что момент  не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.
не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.
Если 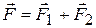 , то на основании известного свойства векторного произведения можно написать
, то на основании известного свойства векторного произведения можно написать
 (6.30)
(6.30)
Это значит, что момент равнодействующей двух или нескольких сил относительно некоторого начала или произвольной точки равен геометрической сумме моментов составляющих сил относительно того же начала.
Как следует из (6.29), модуль момента силы  , где
, где  есть плечо силы. Плечом силы называют длину перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила.
есть плечо силы. Плечом силы называют длину перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила.
Направлен вектор  перпендикулярно к плоскости, в которой лежат сила и точка О, причемнаправление вектора
перпендикулярно к плоскости, в которой лежат сила и точка О, причемнаправление вектора  определяется правилом правого буравчика: поворот головки винта или шурупа с правой нарезкой в направлении силы вызвал бы перемещение винта в направлении вектора
определяется правилом правого буравчика: поворот головки винта или шурупа с правой нарезкой в направлении силы вызвал бы перемещение винта в направлении вектора .
.
8. Момент импульса относительно неподвижного центра
По аналогии с моментом силы, моментом импульса материальной точки (частицы) относительно точки О называется векторная величина
 (6.31)
(6.31)
В этой формуле 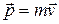 – импульс частицы. Модуль момента импульса
– импульс частицы. Модуль момента импульса
 , (6.32)
, (6.32)
где  называется плечом импульса (рис.6.3).
называется плечом импульса (рис.6.3).
Таким образом, момент импульса равен произведению плеча импульса на модуль вектора импульса.
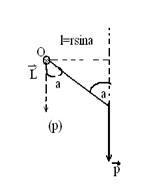
|
Рис. 6.3. Направление и модуль импульса  со временем изменяются. При этом изменяются и плечо, а также модуль и направление вектора со временем изменяются. При этом изменяются и плечо, а также модуль и направление вектора 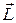 .
Вектор .
Вектор 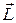 изображен в виде кружка с крестиком внутри. Следовательно, он направлен “от нас”. изображен в виде кружка с крестиком внутри. Следовательно, он направлен “от нас”.
|
Частица обладает моментом импульса независимо от формы траектории, по которой она движется. Рассмотрим два частных случая.
1. Частица движется вдоль прямолинейной траектории (рис.6.4). Модуль момента импульса
 (6.33)
(6.33)
может изменяться только за счет изменения модуля скорости.

| Рис.6.4 |
2. Частица движется по окружности радиуса  (рис.6.5). Модуль момента импульса относительно центра окружности равен и так же, как и в предыдущем случае, может изменяться только за счет изменения модуля скорости. Несмотря на непрерывное изменение направления вектора
(рис.6.5). Модуль момента импульса относительно центра окружности равен и так же, как и в предыдущем случае, может изменяться только за счет изменения модуля скорости. Несмотря на непрерывное изменение направления вектора 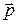 , направление вектора
, направление вектора 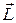 остается постоянным.
остается постоянным.
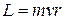 (6.34)
(6.34)
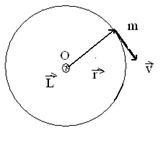
| Рис. 6.5 |
9. Закон сохранения момента импульса
Выясним, от чего зависит изменение момента импульса частицы. С этой целью продифференцируем выражение (6.31) с учетом определения импульса частицы по времени:  .
.
Согласно второму закону Ньютона  – результирующая сил, действующих на частицу. По определению
– результирующая сил, действующих на частицу. По определению  . Поэтому можно написать, что
. Поэтому можно написать, что 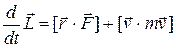 .
.
Второе слагаемое является векторным произведением коллинеарных векторов и поэтому равно нулю. Первое слагаемое представляет собой момент силы относительно той же точки, относительно которой взят момент импульса. Следовательно, мы приходим к соотношению
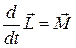 (6.35)
(6.35)
Согласно уравнению (6.35) скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на частицу.
Рассмотрим систему частиц, на которые действуют как внутренние, так и внешние силы. Моментом импульса 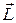 системы относительно точки О называется сумма моментов импульса
системы относительно точки О называется сумма моментов импульса 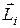 отдельных частиц:
отдельных частиц:
 (6.36)
(6.36)
Дифференцирование по времени дает, что
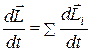 (6.37)
(6.37)
В соответствии с (6.35) для каждой из частиц можно написать равенство  , где
, где  – момент внутренних сил, а
– момент внутренних сил, а  – момент внешних сил, действующих на i-ую частицу. Подставим их в равенство (6.37), получим соотношение
– момент внешних сил, действующих на i-ую частицу. Подставим их в равенство (6.37), получим соотношение  .
.
Каждое из слагаемых в этих суммах представляет собой сумму моментов сил, действующих на i-ую частицу. Суммирование осуществляется по частицам. Если перейти к суммированию по отдельным силам, независимо от того, к какой из частиц они приложены, индекс I в суммах можно опустить.
Можно показать, что сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю. Поэтому получаем, что
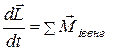 (6.38)
(6.38)
Отсюда видно, что производная по времени от момента импульса системы равна сумме моментов внешних сил.
Если система замкнута, правая часть равенства (6.38) равна нулю и, следовательно, вектор 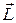 не изменяется со временем. Отсюда вытекает закон сохранения момента импульса, который гласит, что момент импульса замкнутой системы материальных точек остается постоянным.
не изменяется со временем. Отсюда вытекает закон сохранения момента импульса, который гласит, что момент импульса замкнутой системы материальных точек остается постоянным.
Момент импульса сохраняется и для незамкнутой системы материальных точек, если сумма моментов внешних сил равна нулю.
10. Законы сохранения и симметрия пространства и времени
Закон сохранения энергии является следствием однородности времени, закон сохранения импульса – следствием однородности пространства, а закон сохранения момента импульса – следствием изотропии пространства. Это означает, что перечисленные в нем законы сохранения можно получить из второго закона Ньютона, если к нему присоединить свойства симметрии пространства и времени, а именно: однородность пространства и времени, а также изотропию пространства.
Часто говорят, что однородность времени означает равноправие всех моментов времени. Однородность пространства означает, что в пространстве нет выделенных положений, все точки пространства равноправны. Аналогично, изотропия пространства характеризуется отсутствием в нем выделенных направлений, все направления в пространстве эквивалентны. Но такие формулировки слишком неопределенны и при буквальном понимании просто неверны. Направление к центру Земли, например, резко отличается от всякого горизонтального направления. Для альпиниста положения его у подножья и на вершине Эльбруса отнюдь не эквивалентны. Тело на вершине горы, представленное самому себе, может скатиться вниз. Но оно никогда не поднимется от подножья горы к ее вершине, если ему не сообщить надлежащей скорости. Точно так же для человека моменты времени, когда он молод, полон энергии и сил и когда он стар и находится на склоне лет, отнюдь не эквивалентны. Что же такое однородность времени, однородность и изотропия пространства?
Однородность времени означает, что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то, начиная с этих моментов, все явления в ней будут протекать совершенно одинаково.
Однородность пространства означает, что если замкнутую систему тел перенести из одного места пространства в другое, поставив при этом все тела в ней в те же условия, в каких они находились в прежнем положении, то это не отразится на ходе всех последующих явлений. В том же смысле надо понимать и изотропию пространства, только вместо переноса замкнутой системы надо говорить об ее повороте в пространстве на любой угол.
В связи с этими определениями отметим следующее: под замкнутой системой тел нельзя понимать всю Вселенную. Если поступить так, то перечисленные свойства симметрии пространства и времени стали бы самоочевидными. Но они стали бы и бессодержательными. Ибо говорить о переносе или повороте системы тел можно только по отношению к каким-то другим телам. Речь идет не о всей Вселенной в целом, а о таких ее частях, которые можно рассматривать как (приближенно) замкнутые системы. Отсюда ясно, что свойства симметрии пространства и времени, о которых мы говорили, отнюдь не самоочевидны. На них надо смотреть как на фундаментальные обобщения опытных фактов.
После этих разъяснений обратимся к выводу закона сохранения энергии в механике. Из динамики известно, что работа сил над механической системой равна приращению ее кинетической энергии, т.е.
 (6.39)
(6.39)
Рассмотрим одну материальную точку, находящуюся под действием силы  . Предположим, что проекции силы
. Предположим, что проекции силы  могут быть получены дифференцированием потенциальной функции
могут быть получены дифференцированием потенциальной функции  :
:
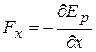 ,
, 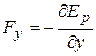 ,
,
Однако сама потенциальная функция  может зависеть явно не только от координат
может зависеть явно не только от координат  рассматриваемой материальной точки, но и от времени t:
рассматриваемой материальной точки, но и от времени t:  . Например, это будет так, когда точка находится в силовом поле других тел, которое меняется во времени. Работа, производимая действующими силами над материальной точкой при перемещении ее вдоль некоторой кривой из положения 1 в положение 2, представляется интегралом
. Например, это будет так, когда точка находится в силовом поле других тел, которое меняется во времени. Работа, производимая действующими силами над материальной точкой при перемещении ее вдоль некоторой кривой из положения 1 в положение 2, представляется интегралом  , взятым вдоль той же кривой. Прибавим и вычтем под знаком интеграла член
, взятым вдоль той же кривой. Прибавим и вычтем под знаком интеграла член  . Тогда имеем
. Тогда имеем
 .
.
Под первым интегралом находится полный дифференциал потенциальной функции  . Поэтому
. Поэтому
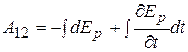 (6.40)
(6.40)
В таком виде последнее равенство справедливо и для системы материальных точек. Поэтому дальнейшие рассуждения не связаны с предположением о том, что система состоит из одной материальной точки. После интегрирования (6.40) получаем
 (6.41)
(6.41)
Комбинация этой формулы с (6.38) приводит к соотношению
 (6.42)
(6.42)
До сих пор мы не использовали условие замкнутости системы и свойства однородности времени, поэтому наши рассуждения применимы и для незамкнутых систем. Допустим теперь, что система замкнута. Тогда ввиду однородности времени функция  не может явно зависеть от времени, т.е.
не может явно зависеть от времени, т.е.  .
.
В результате получим
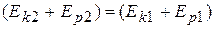 , (6.43)
, (6.43)
т.е. уравнение, выражающее закон сохранения механической энергии.
Докажем закон сохранения импульса. Допустим, что механическая система замкнута. Все силы 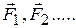 , действующие на материальные точки системы, являются силами внутренними, внешних сил нет. Перенесем систему из произвольного положения 1 в другое произвольное положение 2, чтобы все материальные точки ее претерпели одно и то же перемещение
, действующие на материальные точки системы, являются силами внутренними, внешних сил нет. Перенесем систему из произвольного положения 1 в другое произвольное положение 2, чтобы все материальные точки ее претерпели одно и то же перемещение  и притом так, чтобы их скорости остались прежними по величине и направлению. Ввиду однородности пространства на такое перемещение не требуется затраты работы. Но эта работа представляется скалярным произведением
и притом так, чтобы их скорости остались прежними по величине и направлению. Ввиду однородности пространства на такое перемещение не требуется затраты работы. Но эта работа представляется скалярным произведением  Значит, она равно нулю, каково бы ни было перемещение. Отсюда следует, что для замкнутой системы
Значит, она равно нулю, каково бы ни было перемещение. Отсюда следует, что для замкнутой системы  А это есть как раз то условие, при выполнении которого из второго закона Ньютона получается закон сохранения импульса.
А это есть как раз то условие, при выполнении которого из второго закона Ньютона получается закон сохранения импульса.
Закон сохранения момента импульса для замкнутой системы доказывается в точности так же. Используя изотропию пространства можно доказать, что геометрическая сумма моментов внутренних сил, действующих в системе, равна нулю:  . Отсюда немедленно следует рассматриваемый закон.
. Отсюда немедленно следует рассматриваемый закон.
Контрольные вопросы
1. Что называется механической работой?
2. Как связаны между собой работа и энергия?
3. Напишите формулы для расчета работы постоянной и переменной силы?
4. Какую работу совершает равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?
5. Что называется мощностью? Выведите ее формулу.
6. Назовите единицы энергии, работы и мощности?
7. Какова связь между кинетической энергией материальной точки и работой приложенных к точке сил?
8. Как связана потенциальная энергия материальной точки с работой консервативных сил?
9. Работа силы, действующей на материальную точку, на любом пути равна нулю. Что можно сказать о взаимном направлении силы и скорости материальной точки?
10. Сила, действующая на материальную точку, изменяется по закону  , а скорость точки – по закону
, а скорость точки – по закону  . Чему равна мощность в момент
. Чему равна мощность в момент  ?
?
11. Покажите, что если построить кривую, выражающую кинетическую энергию материальной точки как функцию пройденного пути, то сила, действующая в каждой точке в направлении перемещения, будет измеряться тангенсом угла наклона касательной в данной точке кривой энергии к оси абсцисс.
12. Являются ли силы трения консервативными?
13. Чем отличаются консервативные силы от неконсервативных?
14. В чем физический смысл потенциальной энергии?
15. Сформулируйте закон сохранения полной механической энергию. Назовите условия, при которых выполняется этот закон.
16. Какой удар называется центральным?
17. Чем отличается абсолютно упругий удар от абсолютно неупругого?
18. Определите скорости тел после абсолютно упругого и абсолютно неупругого ударов.
19. Два шара одинаковой массы сталкиваются, причем удар абсолютно упругий, но не центральный. Докажите, что в этом случае угол между направлениями скоростей шаров после удара равен 900?
20. Шар массой  налетает со скоростью
налетает со скоростью 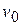 на неподвижный шар массой
на неподвижный шар массой  , причем
, причем  . Удар абсолютно упругий, но не центральный. На какой максимальный угол может отклониться ударяющий шар?
. Удар абсолютно упругий, но не центральный. На какой максимальный угол может отклониться ударяющий шар?
21. Шар массой  налетает со скоростью
налетает со скоростью 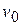 на неподвижный шар массой
на неподвижный шар массой  . Удар абсолютно упругий и центральный. Скорости шаров после удара соответственно равны
. Удар абсолютно упругий и центральный. Скорости шаров после удара соответственно равны  и
и  . Каким соотношениям масс соответствуют следующие значения скорости:
. Каким соотношениям масс соответствуют следующие значения скорости:  ,
,  >0,
>0,  <0?
<0?
22. Что называют моментом силы относительно произвольной точки?
23. Как найти направление вектора момента силы?
24. Докажите, что момент  не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.
не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.
25. Что называется плечом силы?
26. Что называют моментом импульса?
27. Как найти направление вектора момента импульса?
28. Что называется плечом импульса?
29. Может ли обладать моментом импульса материальная точка, движущаяся по прямолинейной траектории?
30. Стоящий на полу пылесос при включении поворачивается в первый момент на небольшой угол. Почему это происходит?
31. Что такое однородность времени, однородность и изотропия пространства?
32. Какие дополнительные ограничения накладывает на вид потенциальной энергии изотропия пространства?
33. Выведите закон сохранения энергии, используя свойства однородности времени.
34. Выведите закон сохранения импульса, используя свойства однородности пространства.
35. Выведите закон сохранения момента импульса, используя свойства изотропии пространства.
Лекция №7. Механика твердого тела
1. Понятие об абсолютно твердом теле
Под абсолютно твердым телом в механике понимают тело, расстояния между любыми двумя материальными точками которого неизменны. Иначе говоря, форма и размеры его не изменяются, каковы бы ни были действующие на это тело силы. Здесь, как и вообще в классической механике, под материальными точками понимают не атомы или молекулы, а достаточно малые макроскопические части, на которые мысленно можно разделить рассматриваемую механическую систему. Естественно, такое представление об абсолютно твердом теле является абстракцией, применимой к тем случаям движения реальных тел, когда изменение формы и размеров этих тел под действием сил пренебрежимо мало. Допустима или нет такая, как и всякая другая идеализация – это определяется не только свойствами реальных тел, но и содержанием тех вопросов, на которые надо получить ответ. В дальнейшем для краткости вместо «абсолютно твердого тела» мы будем говорить только «твердое тело».
2. Твердое тело как система материальных точек
Разбив тело на элементарные массы  можно представить его как систему материальных точек, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием как внутренних сил, обусловленных её взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил. Например, если тело находится в поле сил земного тяготения, на каждую массу тела
можно представить его как систему материальных точек, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием как внутренних сил, обусловленных её взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил. Например, если тело находится в поле сил земного тяготения, на каждую массу тела  будет действовать внешняя сила равная
будет действовать внешняя сила равная  . Однако сумма всех внутренних сил, действующих в системе, равна нулю.
. Однако сумма всех внутренних сил, действующих в системе, равна нулю.
Ранее было показано, что система материальных точек может характеризоваться центром масс системы, координаты которого определяются радиусом-вектором
 (7.1)
(7.1)
Здесь  – масса точки с номером i,
– масса точки с номером i,  – радиус-вектор, определяющий положение этой массы, а
– радиус-вектор, определяющий положение этой массы, а  – полная масса системы точек.
– полная масса системы точек.
Выражение (7.1) не является вполне однозначным, поскольку каждый из векторов  можно проводить в любую из точек
можно проводить в любую из точек  -й элементарной массы. Чтобы устранить эту неопределенность, нужно взять предел выражения (7.1) при условии, что все из
-й элементарной массы. Чтобы устранить эту неопределенность, нужно взять предел выражения (7.1) при условии, что все из  стремятся к нулю:
стремятся к нулю: 
Таким образом,  , (7.2)
, (7.2)
где интегрирование производится по всему телу.
Выражение (7.2) зависит от распределения массы по объему тела. Это распределение характеризуется плотностью вещества 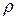 . Для неоднородного тела плотность в точке Р определяется выражением
. Для неоднородного тела плотность в точке Р определяется выражением
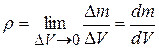 , (7.3)
, (7.3)
где 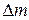 – масса, заключенная в объеме
– масса, заключенная в объеме 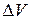 , который включает в себя и точку Р. В формуле (7.3) уменьшение
, который включает в себя и точку Р. В формуле (7.3) уменьшение 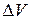 до нуля не означает превращение его в точку. Под
до нуля не означает превращение его в точку. Под 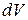 подразумевается физически бесконечно малый объем, т.е. такой объем, который, с одной стороны, достаточно мал для того, чтобы макроскопические свойства (т.е. присущие большой совокупности атомов) вещества можно было считать в его пределах одинаковыми, а с другой стороны, достаточно велик, чтобы не могла проявиться дискретность (прерывистость) вещества.
подразумевается физически бесконечно малый объем, т.е. такой объем, который, с одной стороны, достаточно мал для того, чтобы макроскопические свойства (т.е. присущие большой совокупности атомов) вещества можно было считать в его пределах одинаковыми, а с другой стороны, достаточно велик, чтобы не могла проявиться дискретность (прерывистость) вещества.
Учитывая (7.3), формула (7.2) принимает вид
 , (7.4)
, (7.4)
где интегрирование осуществляется по всему объему тела.
Если тело однородно, плотность во всех точках тела одинакова и ее можно вынести за знак интеграла в (7.4). Тогда
 (7.5)
(7.5)
Таким образом, в случае однородного тела радиус-вектор центра масс представляет собой значение радиус-вектора  , усредненное по всем точкам тела.
, усредненное по всем точкам тела.
Итак, твердое тело эквивалентно системе материальных точек. Поэтому для него справедливо уравнение
 , (7.6)
, (7.6)
где  – результирующая всех внешних сил, действующих на твердое тело.
– результирующая всех внешних сил, действующих на твердое тело.
Таким образом, центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к нему сил.
Уравнение (7.6) дает возможность установить движение центра масс твердого тела, если известна масса тела и действующие на него силы.
3. Поступательное движение твердого тела
Простейший случай движения твердого тела – поступательное движение, т.е. такое движение, при котором все точки твердого тела движутся по подобным траекториям или любая прямая, связанная с телом, остается при его движении параллельной самой себе (рис. 7.1).

Рис.7.1
Обозначим цифрами 1 и 2 две произвольные точки тела, характеризуемые радиусами-векторами  и
и  . Пусть
. Пусть 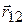 – вектор, проведенный из точки 1 в точку 2 (рис.7.2). Расстояние между рассматриваемыми точками неизменно, поэтому
– вектор, проведенный из точки 1 в точку 2 (рис.7.2). Расстояние между рассматриваемыми точками неизменно, поэтому  . Оно связано с радиусами-векторами точек соотношением
. Оно связано с радиусами-векторами точек соотношением  . Продифференцировав по времени, получим, что
. Продифференцировав по времени, получим, что  , т.е.
, т.е. 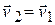 .
.
Аналогично имеем 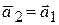 .
.
 Рис.7.2
Рис.7.2
Таким образом, все точки тела получают за один тот же промежуток времени равные по модулю и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Отсюда следует, что при поступательном движении траектории всех точек идентичны и могут быть совмещены параллельным переносом. Поэтому достаточно определить движение одной из точек тела (например, его центра масс) для того, чтобы охарактеризовать полностью движение всего тела.
Следует также отметить, что в случае поступательного движения уравнение (7.6) будет определять ускорение не только центра масс, но и любой другой точки тела.
4. Вращательное движение твердого тела
При вращательном движении все точки тела движутся по подобным траекториям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис.7.3). Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.
 O¢
O¢

Q


 P
P


 O
O
Рис.7.3.
Положение вращающегося тела может быть определено двугранным углом  , между двумя полуплоскостями, проходящими через ось вращения. Одна плоскость
, между двумя полуплоскостями, проходящими через ось вращения. Одна плоскость 
 неподвижна относительно системы координат, другая
неподвижна относительно системы координат, другая  связана с телом и вращается вместе с ним. Знак
связана с телом и вращается вместе с ним. Знак  определяют по правилу правого винта.
определяют по правилу правого винта.
Закон вращения твердого тела определяется уравнением:
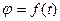 (7.7)
(7.7)
Следуя кинематике движения точки по окружности, рассмотренной в предыдущих разделах, вращательное движение твердого тела можно характеризовать угловой скоростью, т.е. скоростью изменения угла поворота:
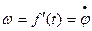 (7.8)
(7.8)
Чтобы охарактеризовать не только быстроту вращения, но также и ориентацию оси вращения в пространстве и направление вращения, вводят векторную величину  , модуль которой определяется формулой (7.8). Направлен вектор
, модуль которой определяется формулой (7.8). Направлен вектор  вдоль оси вращения, причем так, что направление вращения и направление
вдоль оси вращения, причем так, что направление вращения и направление  образуют правовинтовую систему: если смотреть вслед вектору
образуют правовинтовую систему: если смотреть вслед вектору  , вращение представляется происходящим по часовой стрелке. (Рис.7.4). Определенная таким образом векторная величина
, вращение представляется происходящим по часовой стрелке. (Рис.7.4). Определенная таким образом векторная величина  называется угловой скоростью тела.
называется угловой скоростью тела.

 ω
ω
 |
|
R


R
Рис.7.4.
Поскольку направление угловой скорости определяется условно,  является псевдовектором.
является псевдовектором.
Быстрота изменения угловой скорости со временем характеризуется угловым ускорением, т.е.:
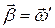 (7 .9)
(7 .9)
Как и угловая скорость, угловое ускорение является псевдовектором.
Как видно из формулы (7.9), направление  определяется направлением изменения угловой скорости
определяется направлением изменения угловой скорости  . Если угловая скорость растет со временем, т.е. вращение ускоренное, направления
. Если угловая скорость растет со временем, т.е. вращение ускоренное, направления  и
и  совпадают, если же вращение замедленное, направления
совпадают, если же вращение замедленное, направления  и
и  противоположные (рис. 7.5).
противоположные (рис. 7.5).
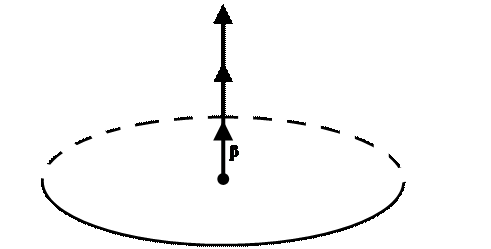
 ω2
ω2
ω1
Рис. 7.5. а)
 ω1
ω1

ω2
 |
β
Рис. 7.5. б)
Найдем связь векторов между  и
и  с величинами
с величинами  и
и 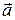 . Возьмем какую-либо произвольную точку этого тела, отстоящую от оси вращения на расстоянии R. Ранее было показано, что линейная и угловая скорости точки связаны соотношением
. Возьмем какую-либо произвольную точку этого тела, отстоящую от оси вращения на расстоянии R. Ранее было показано, что линейная и угловая скорости точки связаны соотношением
 (7.10)
(7.10)
Будем определять положение точек тела с помощью радиус-вектора  , проведенного из точки, лежащей на оси вращения. На рис.7.6 видно, что
, проведенного из точки, лежащей на оси вращения. На рис.7.6 видно, что  . Постановка этого значения в (7.6) дает
. Постановка этого значения в (7.6) дает 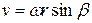 .
.
Это равенство и показанные на рис. 7.6 взаимные направления векторов  ,
,  и
и  дают основания представить
дают основания представить  в виде векторного произведения
в виде векторного произведения  на
на  :
:
 (7.11)
(7.11)

| Рис.7.6 |
Связи модулей нормального 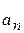 и тангенциального
и тангенциального  ускорений с угловым ускорением
ускорений с угловым ускорением  и угловой скоростью
и угловой скоростью  имеют вид
имеют вид
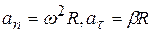 (7.12)
(7.12)
Заметим, что последняя формула в (7.12) справедлива для случая, когда ось вращения, а, следовательно, и вектор  , не изменяет направления в пространстве.
, не изменяет направления в пространстве.
5. Плоское движение твердого тела
Плоским называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Произвольное плоское движение можно представить как совокупность поступательного движения и вращения. Разбиение движения на поступательное и вращательное можно осуществить множеством способов (рис. 7.7).

| 
| 
|
| Рис.7.7 а | Рис.7.7 б | Рис.7.7 в |

| 
| 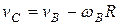
|
В качестве примера рассмотрим качение цилиндра радиуса 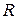 без скольжения по плоскости. Скорости точек цилиндра можно представить как обусловленные: а – одним лишь вращением вокруг оси А с угловой скоростью
без скольжения по плоскости. Скорости точек цилиндра можно представить как обусловленные: а – одним лишь вращением вокруг оси А с угловой скоростью  (рис.7.7 а); б – поступательным движением со скоростью
(рис.7.7 а); б – поступательным движением со скоростью 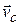 и вращением вокруг оси С с угловой скоростью
и вращением вокруг оси С с угловой скоростью (рис.7.7 б); в – поступательным движением со скоростью
(рис.7.7 б); в – поступательным движением со скоростью 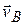 и вращением вокруг оси В с угловой скоростью
и вращением вокруг оси В с угловой скоростью  (рис.7.7 в). Из приведенных на рисунке соотношений легко получить, что
(рис.7.7 в). Из приведенных на рисунке соотношений легко получить, что  . Следовательно, рассмотренные в этом примере способы отличаются значениями скорости поступательного движения, но соответствуют одной и той же угловой скорости
. Следовательно, рассмотренные в этом примере способы отличаются значениями скорости поступательного движения, но соответствуют одной и той же угловой скорости  . Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая, через какую точку проходит ось вращения.
. Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая, через какую точку проходит ось вращения.
Возьмем скорость поступательного движения равной  . Примем одну из точек, лежащих на оси вращения, за начало координат О. Обозначим через
. Примем одну из точек, лежащих на оси вращения, за начало координат О. Обозначим через  – радиус-вектор, проведенный из точки О в данную точку тела. Согласно формуле (7.11), составляющую скорости точек, обусловленную вращением, можно представить в виде
– радиус-вектор, проведенный из точки О в данную точку тела. Согласно формуле (7.11), составляющую скорости точек, обусловленную вращением, можно представить в виде 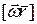 .
.
Следовательно, для скорости точек тела относительно неподвижной системы отсчета получается формула
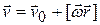 (7.13)
(7.13)

|
| т им- 31.1) ение 1-я |
Особенно удобным оказывается разбиение произвольного плоского движения на поступательное, происходящее со скоростью центра масс 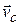 , и вращение вокруг оси, проходящей через этот центр (рис. 7.7 б).
, и вращение вокруг оси, проходящей через этот центр (рис. 7.7 б).
Элементарное перемещение твердого тела при плоском движении всегда можно представить как поворот вокруг так называемой мгновенной оси вращения (рис. 7.7 а). Эта ось может находиться внутри либо вне тела. Положение мгновенной оси относительно неподвижной системы отсчета и относительно тела, вообще говоря, изменяется со временем. В случае, изображенном на рис. 7.7 а-в, мгновенная ось совпадает с линией касания цилиндра с плоскостью (ось А). Эта ось перемещается как по плоскости (т.е. относительно системы отсчета), так и по поверхности цилиндра. Таким образом, плоское движение можно рассматривать как ряд последовательных элементарных вращений вокруг мгновенных осей.
6. Момент силы относительно оси
Как показывает опыт, результат действия силы при вращательном движении зависит от величины силы, от расстояния между осью (или точкой), вокруг которой вращается тело, и точкой приложения силы, а также от направления силы. Действительно, каждый по своему опыту знает, что, закрывая дверь, следует нажимать на неё подальше от оси её вращения. Кроме того, известно, что нельзя закрыть дверь, действуя на неё силой, направленной вверх вдоль оси двери, или силой, перпендикулярной оси в плоскости двери. Дверь закрывают, нажимая на неё перпендикулярно её плоскости. Когда сила приложена к одной из точек твердого тела, вектор момента силы  характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтому момент силы называют также вращающим моментом.
характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтому момент силы называют также вращающим моментом.
Рассмотрим момент силы относительно оси. Проекция вектора  на произвольную ось, проходящую через точку О, называется моментом силы относительно этой оси:
на произвольную ось, проходящую через точку О, называется моментом силы относительно этой оси:
 (7.14)
(7.14)
Пусть твердое тело произвольной формы вращается под действием силы  вокруг некоторой неподвижной оси ОО¢ (рис. 7.8). Тогда все ее точки описывают окружности с центрами на этой оси. В качестве оси может быть взята реальная ось, вокруг которой вращается тело. Но это может быть одна из осей координат и вообще любая воображаемая прямая. Разложим действующую силу
вокруг некоторой неподвижной оси ОО¢ (рис. 7.8). Тогда все ее точки описывают окружности с центрами на этой оси. В качестве оси может быть взята реальная ось, вокруг которой вращается тело. Но это может быть одна из осей координат и вообще любая воображаемая прямая. Разложим действующую силу  на три взаимно перпендикулярные составляющие:
на три взаимно перпендикулярные составляющие: 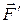 (параллельную оси),
(параллельную оси),  (перпендикулярную оси и лежащую на линии, проходящей через ось) и
(перпендикулярную оси и лежащую на линии, проходящей через ось) и 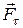 (перпендикулярную
(перпендикулярную 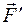 и
и  ). Очевидно, что вращение вызывает только составляющая
). Очевидно, что вращение вызывает только составляющая 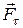 , являющаяся касательной к окружности, описываемой точкой приложения силы. Эта сила называется вращающей силой. Остальные две силы вращения не вызывают. Воспользовавшись определением момента силы относительно точки, представим момент силы
, являющаяся касательной к окружности, описываемой точкой приложения силы. Эта сила называется вращающей силой. Остальные две силы вращения не вызывают. Воспользовавшись определением момента силы относительно точки, представим момент силы относительно точки О в виде
относительно точки О в виде  , где
, где 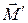 – момент силы
– момент силы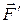 и т.д.
и т.д.
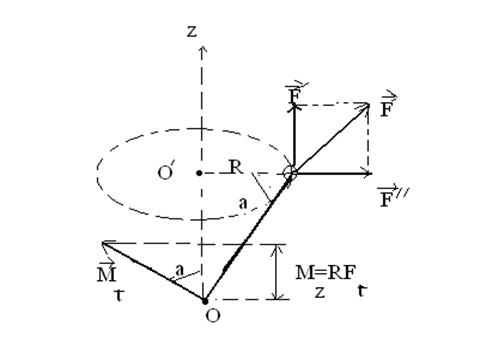
Рис. 7.8
Проекция на ось z вектора  равна сумме проекций моментов составляющих сил. Моменты
равна сумме проекций моментов составляющих сил. Моменты 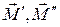 перпендикулярны к оси z , поэтому их проекции равны нулю. Следовательно,
перпендикулярны к оси z , поэтому их проекции равны нулю. Следовательно,
 (7.15)
(7.15)
Таким образом, моментом силы относительно оси (или моментом вращающей силы) будем называть произведение вращающей силы на радиус окружности, описываемой точкой приложения силы.
В общем случае момент силы формально определяется по той же формуле (6.29). Поэтому момент силы относительно оси представляет собой вектор, направленный перпендикулярно плоскости окружности, т.е. вдоль оси по правилу буравчика.
7. Момент пары сил
Две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил (рис.7.9). Расстояние между прямыми, вдоль которых действуют силы, называется плечом пары. Суммарный момент сил относительно точки О равен
 (7.16)
(7.16)

Рис. 7.9.
Учитывая, что  , можно написать
, можно написать
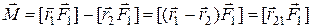 , (7.17)
, (7.17)
где 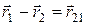 (рис. 7.9).
(рис. 7.9).
Полученное выражение не зависит от положения точки О. Следовательно, момент пары сил относительно любой точки будет одним и тем же. Вектор перпендикулярен к плоскости, в которой лежат силы, а его модуль равен произведению модуля любой из сил на плечо. Силы гравитационного и кулоновского взаимодействия между двумя частицами образуют пару с плечом, равным нулю. Поэтому их суммарный момент относительно любой точки равен нулю. Отсюда следует, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю
 (7.18)
(7.18)
Соответственно, равен нулю и суммарный момент относительно любой оси z:
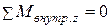 (7.19)
(7.19)
8. Второй закон Ньютона для вращающегося твердого тела
Установим связь между угловым ускорением твердого тела и моментами сил, действующих на него, при вращении этого тела вокруг неподвижной оси. Для этого разобьем тело на элементы, каждый из которых можно принять за материальную точку. Пусть число этих элементов N. Все элементы движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на этой оси и имеют одинаковые ускорения.
Рассмотрим элемент с номером i , масса которого 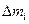 , а радиус окружности, по которой он движется
, а радиус окружности, по которой он движется 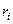 . На этот элемент со стороны других элементов этого же тела действуют внутренние силы
. На этот элемент со стороны других элементов этого же тела действуют внутренние силы  Кроме того, он подвергается действию внешних сил, равнодействующая которых
Кроме того, он подвергается действию внешних сил, равнодействующая которых 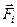 . Для этого элемента справедлив второй закон Ньютона:
. Для этого элемента справедлив второй закон Ньютона:
 (7.20)
(7.20)
Возьмем проекцию этого уравнения на направление касательной к окружности, по которой движется элемент
 (7.21)
(7.21)
Умножим обе части уравнения (7.21) на  и, принимая во внимание, что тангенциальное ускорение элемента представляется в виде
и, принимая во внимание, что тангенциальное ускорение элемента представляется в виде  , получим
, получим
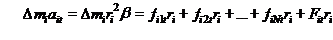 (7.22)
(7.22)
Каждый член в правой части этого уравнения есть момент соответствующей силы относительно оси вращения z. Так, последний член  – момент равнодействующей внешних сил, действующих на элемент тела, а остальные члены –
– момент равнодействующей внешних сил, действующих на элемент тела, а остальные члены – 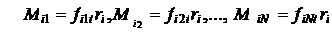 – моменты внутренних сил. Величина
– моменты внутренних сил. Величина  , входящая в левую часть уравнения (7.22), называется моментом инерции
, входящая в левую часть уравнения (7.22), называется моментом инерции  этого элемента относительно оси вращения z.
этого элемента относительно оси вращения z.
С учетом введенных обозначений уравнение (7.22) можно переписать в виде: 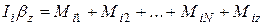 .
.
Аналогичные уравнения можно написать для каждого элемента тела, а затем их сложить. Тогда получим:
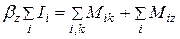 , (7.23)
, (7.23)
где в левой части имеем сумму моментов инерции всех элементов тела относительно оси вращения:  .
.
Он характеризует распределение массы тела относительно оси вращения.
В правой части первое выражение характеризует сумму моментов всех внутренних сил, действующих на все элементы тела, а последнее выражение есть сумма всех действующих на тело внешних сил  .
.
Так как при сложении моментов внутренних сил в уравнении (7.23) все они попарно уничтожаются, уравнение (7.23) принимает вид
 (7.24)
(7.24)
Уравнение (7.24) есть выражение основного закона вращательного движения: Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на его угловое ускорение.
9. Момент инерции твердого тела
Из формулы (7.24) видно, что угловое ускорение, сообщаемое телу вращающим моментом, зависит от момента инерции тела; чем больше момент инерции, тем меньше угловое ускорение. Следовательно, момент инерции характеризует инерционные свойства тела при вращательном движении, как и масса при поступательном движении. В отличие от массы тела момент инерции зависит от радиуса окружности, описываемой точкой приложения силы, а, следовательно, от выбора оси вращения.
Из формулы следует, что единицей измерения момента инерции является кг.мІ.
Из определения момента инерции
 (7.25)
(7.25)
видно, что момент инерции есть величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей:
 (7.26)
(7.26)
Момент инерции существует безотносительно к вращению. Каждое тело независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.
Для неоднородных тел и тел неправильной формы момент инерции определяют экспериментально, а для однородных тел геометрически правильной формы – посредством интегрирования.
Как было ранее указано, в силу формулы (7.3) элементарная масса 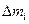 равна произведению плотности тела
равна произведению плотности тела  в данной точке на соответствующий элементарный объем:
в данной точке на соответствующий элементарный объем: 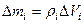 .
.
Следовательно, момент инерции можно представить в виде: 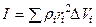 .
.
Если плотность r тела постоянна, её можно вынести за знак суммы задача нахождения моментов инерции сводится к интегрированию:
 (7.27)
(7.27)
Интегралы в (7.27) берутся по всему объему тела. Величины r и r в этих интегралах являются функциями точки.
В качестве примера вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 7.10).
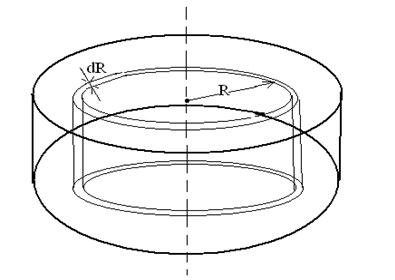
Рис. 7.10.
Разобьем диск на кольцевые слои толщиной  . Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном
. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном  . Объем такого слоя равен
. Объем такого слоя равен  , где
, где  – толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова, (7.27) можем вынести за знак интеграла:
– толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова, (7.27) можем вынести за знак интеграла:  , где
, где  – радиус диска.
– радиус диска.
Так как масса диска  , то получим
, то получим
 (7.28)
(7.28)
Для однородных и симметричных тел обычно основной осью вращения является ось симметрии. В этом случае момент инерции, как мы видели, легко вычисляется.
Для некоторых тел правильной формы значение моментов инерции относительно осей, проходящих через центр их симметрии приведены в таблице 2.
Таблица 2
| Форма тела | Расположение оси | Величина момента инерции |
| Обруч | 
| 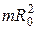
|
| Цилиндр | 
| 
|
| Шар | 
| 
|
| Примечание: m – масса тела, R0 – его радиус |

10. Теорема Штейнера
Рассмотрим произвольное тело и две параллельные друг другу оси, одна из которых (ось С) проходит через центр масс тела, а другая (ось О) отстоит от первой на расстояние а (рис. 7.11). Выберем оси координат  и
и  так, как показано на рис. 7.11.
так, как показано на рис. 7.11.

Рис. 7.11
Момент инерции относительно оси О определяется выражением
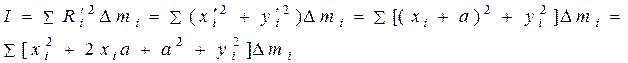
Разобьем это выражение на три суммы: 


Первая сумма представляет собой момент инерции  относительно оси, проходящей через центр масс. Сумма
относительно оси, проходящей через центр масс. Сумма  дает массу тела
дает массу тела 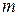 . Наконец,
. Наконец, 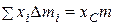 , где
, где  – координата центра масс, которая при сделанном выборе начала координат равна нулю. Таким образом, мы приходим к соотношению:
– координата центра масс, которая при сделанном выборе начала координат равна нулю. Таким образом, мы приходим к соотношению:
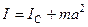 (7.29)
(7.29)
Это соотношение выражает теорему Штейнера, которая гласит, что момент инерции  относительно произвольной оси равен сумме момента инерции
относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведением массы т тела на квадрат расстояния а между осями.
относительно оси, параллельной данной и проходящей через центр масс тела, и произведением массы т тела на квадрат расстояния а между осями.
В соответствии с теоремой Штейнера момент инерции диска относительно оси ОґОґ, отстоящей на расстоянии 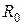 от оси, проходящей через центр масс, равен найденному нами моменту инерции (7.28) относительно оси, проходящей через центр диска, плюс
от оси, проходящей через центр масс, равен найденному нами моменту инерции (7.28) относительно оси, проходящей через центр диска, плюс  :
:  .
.
11. Закон сохранения момента импульса при вращательном движении
Сравним попарно между собой законы и формулы механики поступательного движения и механики вращательного движения: второй закон Ньютона – с основным законом динамики вращения, закон изменения импульса – с законом изменения момента импульса при вращении, выражение линейной скорости – с угловой скоростью и т.д. Бросается в глаза большое сходство в формулировках сравниваемых законов и в структуре сравниваемых формул. Каждой физической величине, характеризующей поступательное движение, соответствует определенная физическая величина, характеризующая вращательное движение. Эти примеры для наглядности представлены в таблице.
| Поступательное движение | Вращательное движение |
Время…………………………..t
Радиус-вектор………………… Линейная скорость …………..
Линейная скорость ………….. Линейное ускорение …………
Линейное ускорение …………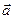 Масса………………………….
Масса…………………………. Сила…………………………...
Сила…………………………... Второй закон Ньютона
Второй закон Ньютона 
| Время…………………………t
Угол поворота……………… Угловая скорость…………...
Угловая скорость…………...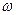 Угловое ускорение…………
Угловое ускорение…………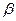 Момент инерции……………
Момент инерции…………… Момент силы относительно оси
Момент силы относительно оси
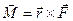 Уравнение моментов
Уравнение моментов 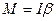
|
Обнаруженное сходство с законами поступательного движения характерно для всех законов вращательного движения. Пользуясь этим, напишем закон вращательного движения, аналогичный закону сохранения импульса материальной точки:
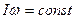 , (7.30)
, (7.30)
или для системы тел:
 (7.31)
(7.31)
Выражение (7.31) носит название закона сохранения момента импульса: в изолированной системе сумма моментов импульса всех тел – величина постоянная.
Из формулы (7.30) следует, что изменение момента инерции тела должно сопровождаться изменением угловой скорости вращения тела: увеличение (уменьшение) момента инерции вызывает соответствующее уменьшение (увеличение) угловой скорости. Это следствие рассматриваемого закона доказывает в частности «скамья Жуковского».
Человек с расставленными в стороны руками вращается, стоя на скамье Жуковского. Затем он быстро опускает руки. При этом его момент инерции уменьшается, а угловая скорость увеличивается. На законе сохранения импульса основаны акробатический прием «сальто-мортале», балетный прием «пируэт» и т.п. Все свободные гироскопы действуют на основе этого закона: вращающаяся с большой скоростью масса сохраняет постоянным ось своего вращения. Этим объясняется устойчивость оси Земли, вертикальная устойчивость движущегося велосипеда и т.п.
12. Кинетическая энергия вращающегося тела
По аналогии с поступательным движением запишем выражение: 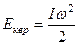 , где
, где  – момент инерции,
– момент инерции, 
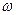 – угловая скорость вращения тела.
– угловая скорость вращения тела.
Действительно, кинетическая энергия одной частицы вращающегося тела массой  , движущейся со скоростью
, движущейся со скоростью  по окружности радиусом
по окружности радиусом 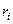 , равна
, равна  , где
, где  – момент инерции частицы,
– момент инерции частицы, 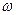 – угловая скорость вращения тела. Тогда, суммируя энергии всех частиц, составляющих тело, получим выражение кинетической энергии вращающегося тела:
– угловая скорость вращения тела. Тогда, суммируя энергии всех частиц, составляющих тело, получим выражение кинетической энергии вращающегося тела:
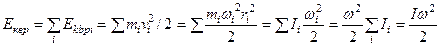
За счет кинетической энергии вращения тело может совершать работу. Эта работа должна равняться изменению кинетической энергии вращения  , где
, где  и
и 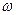 – начальная и конечная угловые скорости вращения. Кинетическая энергия вращающихся тел используется в технике, например, при внезапном увеличении нагрузки машина не останавливается, а совершает работу за счет запаса кинетической энергии вращения маховика.
– начальная и конечная угловые скорости вращения. Кинетическая энергия вращающихся тел используется в технике, например, при внезапном увеличении нагрузки машина не останавливается, а совершает работу за счет запаса кинетической энергии вращения маховика.
Найдем работу, совершаемую внешней силой при вращении твердого тела. Рассмотрим частный случай, когда сила направлена по касательной к окружности, по которой движется точка приложения силы (рис. 7.12). В этом случае сила  и перемещение
и перемещение  точки ее приложения коллинеарны. Элементарная работа
точки ее приложения коллинеарны. Элементарная работа
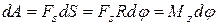 (7.32)
(7.32)
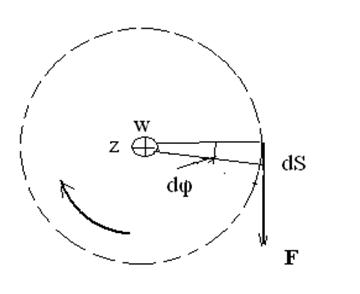
| Рис.7.12 |
Поскольку направления оси  и вектора
и вектора  совпадают, формулу (7.32) можно представить в виде
совпадают, формулу (7.32) можно представить в виде
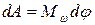 , (7.33)
, (7.33)
где 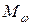 – проекция вектора
– проекция вектора  на направление вектора
на направление вектора  .
.
13. Кинетическая энергия тела при плоском движении
Представим плоское движение тела как наложение поступательного движения со скоростью 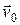 некоторой точки О и вращения вокруг оси, проходящей через эту точку, с угловой скоростью
некоторой точки О и вращения вокруг оси, проходящей через эту точку, с угловой скоростью  . В этом случае скорость i-ой элементарной массы тела определяется формулой
. В этом случае скорость i-ой элементарной массы тела определяется формулой
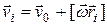 , (7.34)
, (7.34)
где  – радиус-вектор i-ой массы, проведенной из точки О (рис. 7.13).
– радиус-вектор i-ой массы, проведенной из точки О (рис. 7.13).

Рис. 7.13
Кинетическая энергия i-ой элементарной массы равна
 (7.35)
(7.35)
Возведение в квадрат (7.34) с учетом (7.35) дает
 .
.
Просуммировав по всем элементарным массам, найдем кинетическую энергию тела: 
Разобьем полученное выражение на три слагаемых, вынося при этом постоянные множители за знак суммы:
 (7.36)
(7.36)
Сумма элементарных масс даст массу тела  Следовательно, первое слагаемое равно
Следовательно, первое слагаемое равно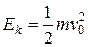 .
.
Третье слагаемое в (7.36) равно  , где
, где  – момент инерции тела относительно оси вращения О.
– момент инерции тела относительно оси вращения О.
Второе слагаемое можно представить в виде  , где
, где  – радиус-вектор, центра масс, проведенный из точки О.С учетом сказанного можно написать, что
– радиус-вектор, центра масс, проведенный из точки О.С учетом сказанного можно написать, что 
В первое слагаемое входят только величины, характеризующие поступательное движение, в третье – только величины, характеризующие вращательное движение. Второе же слагаемое содержит величины, характеризующие как поступательное, так и вращательное движение.
Если в качестве точки О взять центр масс тела С, то  будет равен нулю и последняя формула упростится:
будет равен нулю и последняя формула упростится:  , где
, где 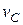 – скорость центра масс,
– скорость центра масс,  – момент инерции тела относительно оси, проходящей через центр масс.
– момент инерции тела относительно оси, проходящей через центр масс.
Таким образом, если разбить плоское движение тела на поступательное со скоростью центра масс и вращение вокруг оси, проходящей через центр масс, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только величинами, характеризующими поступательное движение, а другое – только величинами, характеризующими вращение.
14. Свободные оси вращения
Существуют такие оси вращения тел, которые не изменяют своей ориентации вращения в пространстве без действия на нее внешних сил. Эти оси называются свободными осями вращения (или осями свободного вращения). Можно показать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называютсяглавными осями инерции тела.Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис. 7.14).

Рис. 7.14
Для однородного цилиндра одной из главных осей инерции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоскости, перпендикулярной геометрической оси цилиндра. Главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через центр масс.
Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения.
Вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около осей со средним моментом – неустойчивым. Так, если тело, имеющее форму параллелепипеда, подбросить, одновременно приведя его во вращение, то он, падая, будет устойчиво вращаться вокруг осей 1 и 2.
15. Гироскоп
Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике, наиболее интересны в этом плане гироскопы.
Гироскопом (или волчком) называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии. У симметричного тела направления момента импульса 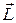 и угловой скорости
и угловой скорости  совпадают, поэтому
совпадают, поэтому  . Вследствие массивности гироскопа его момент инерции очень велик, велика также угловая скорость.
. Вследствие массивности гироскопа его момент инерции очень велик, велика также угловая скорость.
Рассмотрим гироскоп, ось которого закреплена одним концом в шарнире О, вокруг которого она может поворачиваться без трения произвольным образом (рис. 7.15).

|
Рис.7.15. Ось гироскопа ОА, ось ВВ и сила F лежат в плоскости чертежа. Векторы Ми  направлены за чертеж. Ось DD перпендикулярна к плоскости чертежа направлены за чертеж. Ось DD перпендикулярна к плоскости чертежа
|
Попытаемся повернуть ось гироскопа ОА вокруг оси DD, подействовав на свободный конец оси силой F в течение времени dt. Однако гироскоп «проявит непослушание» – его ось повернется не вокруг оси DD, а вокруг оси ВВ, приняв положение ОА'. Это, казалось бы, противоестественное поведение гироскопа называют гироскопическим эффектом.
Гироскопический эффект находится в полном согласии с законами механики твердого тела. Действительно, согласно уравнению изменения момента импульса со временем в результате действия силы F в течение времени dt момент импульса L получит приращение  . Обозначим через М – момент силы F относительно точки О. Тогда изменение момента импульса равно
. Обозначим через М – момент силы F относительно точки О. Тогда изменение момента импульса равно  . Новое значение момента импульса, равно
. Новое значение момента импульса, равно  . Оно окажется повернутым вокруг оси ВВ относительно первоначального значения L. Поскольку вектор L направлен вдоль оси гироскопа, вместе с L повернется и ось, перейдя из положения О А в положение О А'.
. Оно окажется повернутым вокруг оси ВВ относительно первоначального значения L. Поскольку вектор L направлен вдоль оси гироскопа, вместе с L повернется и ось, перейдя из положения О А в положение О А'.
Гироскопический эффект является причиной того, что хорошо раскрученный детский волчок не опрокидывается под действием силы тяжести. Это действие приводит лишь к тому, что ось волчка поворачивается, описывая конус. Такое движение оси называется прецессией.
Рассмотрим простейший вид прецессии, называемый регулярной прецессией. Пусть один из концов оси гироскопа закреплен в шаровом шарнире О, позволяющем ей свободно поворачиваться в любом направлении (рис. 7.15). На гироскоп действует сила тяжести, которая лежит в вертикальной плоскости ОАО'. Обозначим через т – массу гироскопа вместе с осью. Момент силы М перпендикулярен к этой плоскости. Пусть b – расстояние от шарнира О до центра масс гироскопа С,  – угол, образованный осью гироскопа с вертикалью. Тогда плечо силы
– угол, образованный осью гироскопа с вертикалью. Тогда плечо силы  . За время dt момент импульса получает приращение
. За время dt момент импульса получает приращение  , в результате чего вертикальная плоскость, в которой лежат ось гироскопа и сила тяжести mg, поворачивается на угол
, в результате чего вертикальная плоскость, в которой лежат ось гироскопа и сила тяжести mg, поворачивается на угол  . Вместе с ней поворачивается и вектор
. Вместе с ней поворачивается и вектор 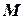 . Расстояние О'А численно равно
. Расстояние О'А численно равно  .
.
Таким образом, на гироскоп действует опрокидывающий момент  . Будем откладывать вектор момента импульса гироскопа L из точки О. В момент времени t вектор L изображается отрезком ОА. За время dt вектор L получит перпендикулярное к нему приращение
. Будем откладывать вектор момента импульса гироскопа L из точки О. В момент времени t вектор L изображается отрезком ОА. За время dt вектор L получит перпендикулярное к нему приращение  ,в результате чего он, оставаясь постоянным по модулю и не изменяя угла
,в результате чего он, оставаясь постоянным по модулю и не изменяя угла  с вертикалью, переходит в положение ОВ. В новом положении имеет место такое же взаимное расположение векторов L и М, какое было в момент t. Поэтому за последующий элемент времени dt вертикальная плоскость, в которой лежит ось гироскопа, снова повернется на угол
с вертикалью, переходит в положение ОВ. В новом положении имеет место такое же взаимное расположение векторов L и М, какое было в момент t. Поэтому за последующий элемент времени dt вертикальная плоскость, в которой лежит ось гироскопа, снова повернется на угол  и т.д. В итоге ось гироскопа будет поворачиваться вокруг вертикальной оси, описывая конус с углом раствора 2
и т.д. В итоге ось гироскопа будет поворачиваться вокруг вертикальной оси, описывая конус с углом раствора 2 . При этом вектор L будет изменяться только по направлению, оставаясь неизменным по модулю. Это объясняется тем, что элементарные приращения
. При этом вектор L будет изменяться только по направлению, оставаясь неизменным по модулю. Это объясняется тем, что элементарные приращения  все время будут перпендикулярными вектору L. Аналогично ведет себя вектор скорости при равномерном движении частицы по окружности. Вектор v получает за время dt перпендикулярное к нему приращение
все время будут перпендикулярными вектору L. Аналогично ведет себя вектор скорости при равномерном движении частицы по окружности. Вектор v получает за время dt перпендикулярное к нему приращение  , где
, где 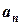 – постоянное по модулю нормальное ускорение. В результате изменяется только направление вектора
– постоянное по модулю нормальное ускорение. В результате изменяется только направление вектора  , модуль же его остается постоянным.
, модуль же его остается постоянным.

| Рис. 7.16. |
Таким образом, в поле сил тяжести ось гироскопа с неподвижной точкой поворачивается вокруг вертикали, описывая конус. В случае, когда  , конус вырождается в плоскость. Такое движение гироскопа называется регулярной прецессией. Угловую скорость прецессии
, конус вырождается в плоскость. Такое движение гироскопа называется регулярной прецессией. Угловую скорость прецессии  можно найти, разделив угол
можно найти, разделив угол  на соответствующее время dt. Из рис. 7.16 следует, что
на соответствующее время dt. Из рис. 7.16 следует, что  .
.
Из соотношения  вытекает, что
вытекает, что . Поэтому
. Поэтому  .
.
Отсюда, с учетом того, что  , a
, a  получаем формулу
получаем формулу
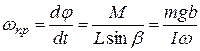 (7.37)
(7.37)
Здесь I – момент инерции вращающихся частей гироскопа,  – угловая скорость вращения гироскопа вокруг своей оси,
– угловая скорость вращения гироскопа вокруг своей оси,  – расстояние oт центра масс гироскопа.
– расстояние oт центра масс гироскопа.
Из формулы (7.37) видно, что угловая скорость прецессии не зависит от угла  , образованного осью гироскопа с направлением вверх по вертикали (этот угол может иметь значения от 0 до
, образованного осью гироскопа с направлением вверх по вертикали (этот угол может иметь значения от 0 до 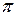 ).
).
Нужно иметь в виду, что формула (7.37) справедлива только при условии, что
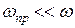 (7.38)
(7.38)
Действительно, прецессирующий гироскоп участвует одновременно в двух вращениях, совершающихся со скоростью  и
и  . Поэтому его момент импульса определяется выражением, более сложным, чем
. Поэтому его момент импульса определяется выражением, более сложным, чем  . Только при соблюдении условия (7.38) можно полагать, что
. Только при соблюдении условия (7.38) можно полагать, что  .
.
Из формулы (7.37) следует, что условие (7.38) эквивалентно условию  , т.е.
, т.е.  .
.
Выражение mgb по порядку величины равно потенциальной энергии гироскопа Ер. Выражение  по порядку есть кинетическая энергия гироскопа Ек.. Поэтому условие справедливости формулы (7.37) можно представить в виде
по порядку есть кинетическая энергия гироскопа Ек.. Поэтому условие справедливости формулы (7.37) можно представить в виде  .
.
Вычислим полную механическую энергию гироскопа. За нуль примем значение потенциальной энергии при  . Будем считать, что
. Будем считать, что  можно пренебречь по сравнению с
можно пренебречь по сравнению с  . Тогда полная механическая энергия гироскопа определяется выражением
. Тогда полная механическая энергия гироскопа определяется выражением  .
.
В отсутствие трения полная энергия сохраняется, следовательно,  также не уменьшается. Отсюда следует, что
также не уменьшается. Отсюда следует, что  = const. К этому результату мы уже пришли ранее.
= const. К этому результату мы уже пришли ранее.
16. Степени свободы и связи абсолютно твердого тела
Число независимых координат, однозначно определяющих положение тела в пространстве, называется степенью свободы. Ясно, что положение точки в пространстве можно характеризовать тремя прямоугольными координатами  . Вместо таких координат можно взять и полярные координаты. Но их будет не более трех. Поэтому говорят, что материальная точка обладает тремя степенями свободы.
. Вместо таких координат можно взять и полярные координаты. Но их будет не более трех. Поэтому говорят, что материальная точка обладает тремя степенями свободы.
Однако не всегда перемещение точки в заданных условиях будет каким угодно. Рассмотрим, например, маленький шарик, привязанный к концу нерастяжимой нити, другой конец которой закреплен. Если нить натянута, то шарик может перемещаться только по поверхности сферы с центром в точке закрепления. Можно привести и другие примеры, в которых материальная точка все время вынуждена находиться на какой-либо заданной поверхности. В таких случаях говорят, что на ее движение наложены связи. Координаты  такой точки должны соответствовать соотношению вида
такой точки должны соответствовать соотношению вида  , который является уравнением рассматриваемой поверхности. Ввиду этого остаются независимыми только две координаты. Третья координата может быть вычислена из уравнения связи
, который является уравнением рассматриваемой поверхности. Ввиду этого остаются независимыми только две координаты. Третья координата может быть вычислена из уравнения связи . В этих случаях точка обладает двумя степенями свободы.
. В этих случаях точка обладает двумя степенями свободы.
Пусть имеется механическая система, состоящая из произвольного числа  материальных точек. Если эти точки движутся без всяких ограничений, то для мгновенного определения их положения надо задать
материальных точек. Если эти точки движутся без всяких ограничений, то для мгновенного определения их положения надо задать 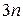 координат. Следовательно, система имеет
координат. Следовательно, система имеет 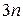 степени свободы. Однако в некоторых случаях свобода перемещения точек ограничена. На
степени свободы. Однако в некоторых случаях свобода перемещения точек ограничена. На 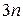 координат налагаются дополнительные условия, называемые связями. Обозначим его
координат налагаются дополнительные условия, называемые связями. Обозначим его  . Следовательно, данная механическая система имеет
. Следовательно, данная механическая система имеет 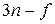 степени свободы.
степени свободы.
Определим число степеней свободы абсолютно твердого тела. Ясно, что для однозначного определения положения твердого тела достаточно задать положение каких-либо трех его координат А, В, С, не лежащих на одной прямой (рис.7.17).

| Рис.7.17 |
Возьмем четвертую точку D. Расстояния AD, BD и CD для рассматриваемого твердого тела известны. Кроме того, при любых движениях твердого тела точка D все время должна находиться по одну и ту же сторону плоскости треугольника ABC. Чтобы определить положение в пространстве точки D, построим по заданным длинам AC, AD, CD треугольник ADC. Чтобы найти положение точки D, будем вращать треугольник ADC вокруг основания AC, пока вершина D не окажется на заданном расстоянии от третьей точки B. Этому условию соответствуют две точки D и Dґ. Но вторая точка не отвечает условию задачи, так как она находится не с той стороны от плоскости треугольника ABC. Таким образом, зная положения трех точек А, В, С, можно геометрическим построением найти положение любой другой точки твердого тела.
Положения трех точек А, В, С можно задать их прямоугольными координатами  ,
,  ,
,  . Эти девять координат не свободны, а связаны тремя соотношениями
. Эти девять координат не свободны, а связаны тремя соотношениями

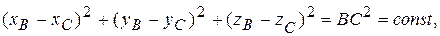

Независимыми остаются только шесть координат, поскольку длины AB, BC и СA не изменяются. Поэтому твердое тело имеет шесть степеней свободы.
При ограничении свободы движения число степеней свободы твердого тела уменьшается. Например, твердое тело, одна из точек которого неподвижно закреплена, может только вращаться вокруг этой неподвижной точки, и имеет три степени свободы. Твердое тело, которое может только вращаться вокруг закрепленной оси, имеет одну степень свободы. Если же твердое тело может скользить вдоль закрепленной оси и одновременно вращаться вокруг нее, то число степеней свободы становится равным двум.
17. Условия равновесия твердого тела. Виды равновесия
Как было указано в предыдущем разделе, твердое тело является механической системой с шестью степенями свободы. Для описания его движения требуется шесть независимых числовых уравнений. Вместо них можно взять два независимых векторных уравнения. Таковыми являются уравнение движения центра масс
 (7.38)
(7.38)
и уравнение моментов
 (7.39)
(7.39)
Если твердое тело покоится, то уравнения (7.38) и (7.39) переходят в уравнения
 (7.40)
(7.40)
 (7.41)
(7.41)
В этих формулах  – результирующая внешних сил,
– результирующая внешних сил, 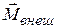 – сумма моментов этих сил относительно оси вращения. Таким образом, равновесие имеет место в том случае, когда результирующая внешних сил и сумма моментов относительно оси вращения равны нулю.
– сумма моментов этих сил относительно оси вращения. Таким образом, равновесие имеет место в том случае, когда результирующая внешних сил и сумма моментов относительно оси вращения равны нулю.
Это – необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может еще двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением вращательного импульса. Так как при равновесии  равна нулю, то момент этих сил
равна нулю, то момент этих сил 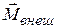 в состоянии равновесия не зависит от положения неподвижного начала О, относительно которого он берется. Поэтому при решении любой задачи на равновесие твердого тела начало О можно выбирать произвольно.
в состоянии равновесия не зависит от положения неподвижного начала О, относительно которого он берется. Поэтому при решении любой задачи на равновесие твердого тела начало О можно выбирать произвольно.
Различают устойчивое и неустойчивое равновесия. Как показывает связь силы с потенциальной энергией, при равенстве нулю результирующих внешних сил в состоянии равновесиявсе производные потенциальной энергии по координатам должны обращаться в нуль. Отсюда следует, что для равновесия необходимо, чтобы потенциальная энергия была стационарна. Стационарность означает, что при всяком выводе системы из состояния равновесия, когда координаты материальных точек получают бесконечно малые приращения, функция потенциальной энергии остается почти постоянной. Точнее, приращения потенциальной функции при таких приращениях координат являются бесконечно малыми более высокого порядка, чем приращения самих координат. В частности, система будет находиться в равновесии, если потенциальная энергия экстремальна, т.е. минимальна или максимальна.
Если потенциальная энергия минимальна, то равновесие будет устойчивым. Диссипативные силы делают равновесие еще более устойчивым. Если потенциальная энергия максимальна, равновесие тела неустойчиво.
Эти выводы остаются справедливыми и для систем, свобода перемещения которых ограничена наложенными связями. Надо только потребовать, чтобы связи были идеальными, т.е. такими, которые не производят работы при любых возможных перемещениях системы. Примером может служить идеально гладкий шарик, надетый на идеально твердую и гладкую спицу, которая задает направление возможного перемещения шарика. Сила, действующая на шарик со стороны спицы, перпендикулярна направлению возможного перемещения и работы не производит.
18. Центр тяжести
На каждую точку частицы твердого тела действует сила тяготения Земли. Все силы тяготения параллельны друг другу, если размеры тела невелики относительно радиуса Земли, и имеют равнодействующую. Оказывается, как бы ни повернули твердое тело, эта равнодействующая будет проходить через одну точку, неизменно связанную с телом. Эта точка называется центром тяжести тела.
Если укрепить тело в точке центра тяжести, то оно будет находиться в равновесии при любом положении тела. Следовательно, сумма моментов сил тяжести всех частиц тела относительно любой горизонтальной оси, проходящей через центр тяжести, равна нулю. Подвешенное так тело после поворота вокруг любой оси, проходящей через центр тяжести, будет оставаться в равновесии, так как равнодействующая сил тяжести проходит через точку закрепления.
Центр масс твердого тела совпадает с его центром тяжести. Поэтому вместо терминов “центр масс” и “центр инерции” употребляют также термин “центр тяжести”. Следовательно, координаты центра тяжести можно найти по формуле, справедливой для радиуса-вектора центра масс, о которой мы говорили в разделе “Центр масс системы материальных точек”. Положение центра тяжести можно вычислить также по формулам (7.40) и (7.41).
Центр тяжести можно определить и экспериментально.
Контрольные вопросы
1. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?
2. Чему равно ускорение центра масс тела, имеющего массу m и находящегося под действием сил  и
и  ?
?
3. От каких величин зависит угловое ускорение тела?
4. Могут ли момент импульса и угловая скорость вращающегося тела быть неколлинеарными?
5. Приведите примеры проявления закона сохранения момента импульса твердого тела.
6. Что такое момент инерции тела?
7. Какова роль момента инерции тела во вращательном движении?
8. Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.
9. Что такое момент импульса материальной точки? Твердого тела? Как определяется направление момента импульса?
10. В чем заключается физическая сущность закона сохранения момента импульса? В каких системах он выполняется? Приведите примеры.
11. Сопоставьте основные уравнения динамики поступательного и вращательного движений, прокомментировав их аналогии.
12. Что такое свободные оси (главные оси инерции)? Какие из них являются устойчивыми?
13. В каком случае кинетическая энергия вращающегося тела определяется формулой  ? Как ее вывести?
? Как ее вывести?
14. Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?
15. Что такое гироскоп? Каковы его основные свойства?
16. Что происходит с угловой скоростью прецессии при уменьшении скорости вращения гироскопа вокруг его оси?
17. Докажите, что угловая скорость прецессии не зависит от угла  .
.
18. Как влияет сила трения на вращение гироскопа?
19. Выведите формулу кинетической энергии твердого тела при плоском движении.
20. Что такое центр тяжести твердого тела. Как экспериментально и теоретически определить положение центра тяжести твердого тела?
21. Как определяется степень свободы твердого тела?
22. Что такое связи?
23. Сформулируйте условия равновесия твердого тела.
Лекция №8. Механика деформируемых тел
1. Упругие силы
Упругие силы действуют со стороны деформированного тела на тело, непосредственно соприкасающееся с этим деформированным телом. Данные силы действуют также со стороны деформированной части тела на другие смежные части этого же тела.
Под деформацией подразумевается изменение взаимного расположения точек тела.
Деформации сопровождаются изменением геометрической формы тела и его размеров.
На данное тело упругими силами могут действовать твердые, жидкие и газообразные тела. Упругие силы в твердых телах возникают как при изменении их формы, так и при изменении объема. В жидкостях упругие силы возникают лишь при изменении объема жидкости. Газ всегда действует упругими силами на стенки сосуда, в котором он находится, величина этих сил зависит от объема сосуда.
Упругие силы представляют собой проявление сил взаимодействия молекул, составляющих твердые, жидкие и газообразные тела. В конечном счете, происхождением они обязаны электрическому взаимодействию между частицами, входящими в состав молекул. Силы молекулярного взаимодействия очень быстро убывают с увеличением расстояния между молекулами и радиус действия их не более 10-7 – 10-8 см. Поэтому упругими силами взаимодействуют между собой только тела, находящиеся в непосредственном контакте.
Упругая сила действует только со стороны деформированного тела. Действительно, если тело не подвергается действию внешних сил, то каждая молекула тела находится в равновесном положении. При деформации тела изменяется положение каждой молекулы относительно соседних. Молекулы, находящиеся от данной молекулы на расстояниях, меньших равновесного, действуют на неё силами отталкивания, а молекулы, находящиеся на расстояниях, больших равновесного, – силами притяжения. В результате действия совокупности молекул, сдвинутых со своих равновесных положений, возникает сила, действующая на тело, непосредственно соприкасающееся с данным. Это и есть упругая сила.
Упругие силы возникают лишь при таких деформациях, когда при прекращении действия на тело внешних сил деформация исчезает, т.е. тело восстанавливает свою первоначальную форму и размеры. Такие деформации называются упругими.
Опыт показывает, что сила упругости  , возникающая при малых деформациях любого вида, пропорциональна величине деформации
, возникающая при малых деформациях любого вида, пропорциональна величине деформации  :
:
 (8.1)
(8.1)
Это положение называется законом Гука.
Коэффициент пропорциональности k зависит от свойств тела, подвергающегося деформации (его размеров, формы, вещества, из которого оно изготовлено), от вида деформации, от выбора величины, характеризующего деформацию, а также от температуры.
В качестве примера тела, действующего на другие тела упругой силой, рассмотрим пружину. Закон Гука для пружины имеет вид:  , где
, где 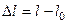 – деформация пружины, равная изменению её длины, причем
– деформация пружины, равная изменению её длины, причем  – длина недеформированной пружины,
– длина недеформированной пружины,  – длина деформированной (растянутой или сжатой). Коэффициент
– длина деформированной (растянутой или сжатой). Коэффициент  называется коэффициентом жесткости пружины. Он показывает, какую силу нужно приложить к данной пружине для её растяжения на единицу. Величина этого коэффициента зависит от числа витков, их диаметра, материала проволоки, из которой изготовлена пружина, и диаметра этой проволоки.
называется коэффициентом жесткости пружины. Он показывает, какую силу нужно приложить к данной пружине для её растяжения на единицу. Величина этого коэффициента зависит от числа витков, их диаметра, материала проволоки, из которой изготовлена пружина, и диаметра этой проволоки.
Направления сил упругости и деформаций противоположны. Рассмотрим пружину, один конец которой закреплен, а на другой конец прикреплено тело. Выберем систему координат, одна из осей которой (например, ось Х) направлена вдоль пружины, а начало её связано с концом недеформированной пружины. Тогда при смещении тела вдоль оси Х на некоторое расстояние деформация пружины, прикрепленной к этому телу, будет равна координате  этого тела. В этом случае упругая сила, действующая на тело со стороны пружины, будет иметь проекцию
этого тела. В этом случае упругая сила, действующая на тело со стороны пружины, будет иметь проекцию 
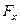 , которая согласно закону Гука равна
, которая согласно закону Гука равна
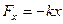 (8.2)
(8.2)
Знак минус показывает, что при смещении тела в положительном направлении оси Х проекция силы на эту же ось имеет отрицательное направление.
Упругие силы относятся к центральным силам, так как при любом положении тела деформация тела определяется координатой х.
Действие на твердое тело упругих сил со стороны других твердых тел проявляется в виде силы нормального давления. Например, на тело, лежащее на столе, действует упругая сила со стороны стола.
Твердые тела, действующие на некоторое тело упругими силами, могут ограничивать его движение. Например, такими ограничивающими движение телами являются рельсы, плоскости, по которым скользит тело, нити, связывающие тело с другими телами, оси, закрепленные в подшипниках и т.д. Тела, ограничивающие движение данного тела, называют связями, а упругие силы, которыми они действуют на это тело – силами связей или силами реакций. Измерить их практически невозможно, однако можно найти при помощи законов Ньютона, учитывая ограничения, накладываемые этими связями на движение тел. Например, тело соскальзывает с наклонной плоскости без трения. На тело действует сила тяжести, направленная вниз, и упругая сила связи (реакции) со стороны наклонной плоскости, направленная перпендикулярно поверхности соприкосновения тела и плоскости в сторону тела. Сила связи в уравнениях Ньютона фигурирует в качестве неизвестных.
2. Виды упругих деформаций
Деформации зависят от многих причин:
- от формы и размеров деформируемого тела;
- от величины, направления и точек приложения внешних сил;
- от свойств вещества, из которого изготовлено тело;
- от того, движется ли тело или оно неподвижно;
- от температуры.
Все эти причины могут комбинироваться самым различным образом. Поэтому виды деформаций весьма разнообразны.
Мы будем считать, что:
- деформированное тело неподвижно;
- деформируемое тело однородное, т.е. свойства вещества во всех точках тела одинаковы;
- температура деформируемого тела во всех его точках одинакова и постоянна;
- деформации малы, т.е. смещения точек тела относительно друг друга малы по сравнению с расстоянием между этими точками.
Существует несколько видов деформаций тел: одностороннее сжатие или растяжение, всестороннее растяжение или сжатие, кручение, сдвиг, изгиб. Каждый вид деформации вызывает появление соответствующей силы упругости. Однако все виды деформаций можно свести к двум видам: растяжению (или сжатию) и сдвигу.
Рассмотрим эти основные деформации несколько подробнее.
Пусть стержень длины  и поперечного сечения
и поперечного сечения 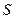 подвешен (рис. 8.1). Под влиянием деформирующей силы
подвешен (рис. 8.1). Под влиянием деформирующей силы  он растягивается, приобретает новую длину
он растягивается, приобретает новую длину 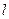 и в нем возникает сила упругости
и в нем возникает сила упругости  .
.

| Рис.8.1. |
Мерой деформации растяжения может служить величина  – изменение длины стержня, которую называют абсолютным удлинением. Другой величиной, характеризующей деформацию стержня, является относительное удлинение (удлинение каждой единицы длины стержня):
– изменение длины стержня, которую называют абсолютным удлинением. Другой величиной, характеризующей деформацию стержня, является относительное удлинение (удлинение каждой единицы длины стержня): .
.
Опыт показывает, что относительное удлинение стержня пропорционально деформирующей силе и обратно пропорционально площади поперечного сечения
 , (8.3)
, (8.3)
где a – коэффициент упругости при растяжении (сжатии) или коэффициент продольного удлинения (сжатия), зависящий только от материала стержня.
Отношение силы к сечению, на котором она действует, называется напряжением в данном сечении. Деформацию растяжения вызывает сила, нормальная к площади сечения, а возникающее напряжение называется нормальным напряжением рn:
рn =  (8.4)
(8.4)
В физической литературе напряжение, определяемое по формуле (8.4), называют также натяжением, если тело растягивают. Его обозначают буквой Т.
Тогда закон Гука для деформации растяжения (сжатия) примет вид:
 (8.5)
(8.5)
При рn=1 a =e, т.е. коэффициент упругости численно равен относительному удлинению стержня, происходящему под действием единичного напряжения.
Для характеристики упругих свойств материала пользуются величиной  , которая называется модулем упругости или модулем Юнга. Эта величина измеряется в Паскалях. Согласно формулам (8.4) и (8.5),
, которая называется модулем упругости или модулем Юнга. Эта величина измеряется в Паскалях. Согласно формулам (8.4) и (8.5), 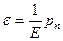
В качестве характеристики деформации сдвига берется величина
Е = рnпри e=1, т.е. модуль Юнга численно равен тому напряжению, которое вызывает единичное относительное удлинение, или абсолютное удлинение, равное длине стержня. Решив уравнение (8.3) относительно деформирующей силе и учитывая формулы (8.4) и (8.5), получим выражение
 (8.6)
(8.6)
где k– постоянный для данного стержня коэффициент. Соотношение (8.6) выражает закон Гука для стержня.
Опыт показывает, что под действием растягивающей силы изменяются не только продольные, но и поперечные размеры стержня. Если сила растягивающая, то поперечные размеры стержня уменьшаются. Пусть до деформации толщина стержня равна а0, а после деформации – а. Если сила растягивающая, то величина  называется относительным поперечным сжатием стержня. Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона:
называется относительным поперечным сжатием стержня. Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона: 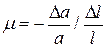 .
.
Рассмотрим деформацию сдвига. Возьмем однородное тело, имеющее форму прямоугольного параллелепипеда, нижнюю грань закрепим, а к его верхней грани приложим силу F,параллельную нижней грани.

| Рис.8.2 |
Если действие силы Fбудет равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникнет тангенциальное напряжение, т.е. напряжение, при котором сила направлена по касательной к поверхности, на которую она действует:  , где S– площадь грани. Под действием напряжений тело деформируется так, что одна грань сместится относительно другой на некоторое расстояние а. Если тело мысленно разбить на элементарные, параллельные рассматриваемым граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев. Поэтому деформация такого типа называется сдвигом.
, где S– площадь грани. Под действием напряжений тело деформируется так, что одна грань сместится относительно другой на некоторое расстояние а. Если тело мысленно разбить на элементарные, параллельные рассматриваемым граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев. Поэтому деформация такого типа называется сдвигом.
При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, повернется на некоторый угол j. В качестве характеристики деформации сдвига берется величина
 , (8.7)
, (8.7)
называемая относительным сдвигом. При упругих деформациях угол jбывает очень мал. Поэтому можно положить tgj»j. Следовательно, относительный сдвиг gоказывается равным углу сдвига j.
Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению:  .
.
Коэффициент Gзависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 450 (tgj=1), если бы при сколь угодно больших деформациях не был превзойден предел упругости. Измеряется Gкак и Е в Паскалях. Для большинства упругих тел G@0,4E.
3. Упругие и пластические деформации.
Предел упругости и предел прочности
Деформации твердых тел подчиняются закону Гука до известного предела. Обозначим в общем случае напряжение через  . Связь между относительной деформацией и напряжением
. Связь между относительной деформацией и напряжением  представляется в виде диаграммы напряжений, которую мы качественно рассмотрим для твердого тела (рис.8.3).
представляется в виде диаграммы напряжений, которую мы качественно рассмотрим для твердого тела (рис.8.3).
Из рисунка видно, что линейная зависимость, установленная Гуком, выполняется лишь для упругих тел при малых относительных деформациях, а именно до так называемого предела пропорциональности  , соответствующая области ОА. При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость
, соответствующая области ОА. При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость  уже не линейна) и до предела упругости
уже не линейна) и до предела упругости остаточные деформации не возникают.
остаточные деформации не возникают.
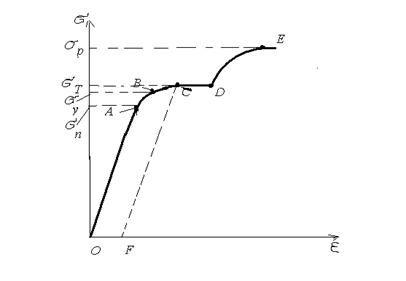
| Рис.8.3 |
Предел упругости практически совпадает с точкой В. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ОВ, а параллельной ей – СF. Фигура OABCFO называется областью упругого гистерезиса. Напряжение, при котором появляется заметная остаточная деформация (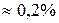 ), называется пределом текучести
), называется пределом текучести  . Ему соответствует точка С на кривой. В области СD деформация возрастает без увеличения напряжения, т.е. тело как бы “течет”. Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, если же она практически отсутствует – хрупкими. Деформация не исчезает и после прекращения воздействия на тело, когда она достаточно велика. Тогда деформацию называют пластической (текущей), в области которой лежит точка С.
. Ему соответствует точка С на кривой. В области СD деформация возрастает без увеличения напряжения, т.е. тело как бы “течет”. Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, если же она практически отсутствует – хрупкими. Деформация не исчезает и после прекращения воздействия на тело, когда она достаточно велика. Тогда деформацию называют пластической (текущей), в области которой лежит точка С.
При дальнейшем растяжении происходит разрушение тела. На рисунке в точке Е наступает разрыв. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности ( ).
).
Отметим, что и в случае упругой деформации первоначальная форма тела восстанавливается не мгновенно, а через некоторое время, измеряемое иногда часами и даже днями. Это явление называется упругим последействием.
4. Всестороннее растяжение и сжатие
Допустим, что однородное изотропное твердое тело имеет форму прямоугольного параллелепипеда, к противоположным граням которого приложены силы  , нормальные к этим граням. Соответствующие им натяжения обозначим
, нормальные к этим граням. Соответствующие им натяжения обозначим 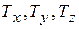 (рис.8.4). Определим деформации, которые возникнут под действием этих сил. Будем предполагать деформации малыми.
(рис.8.4). Определим деформации, которые возникнут под действием этих сил. Будем предполагать деформации малыми.
Направим координатные оси параллельно ребрам параллелепипеда. Пусть  – длины этих ребер. Если бы действовала только сила
– длины этих ребер. Если бы действовала только сила  , то ребро
, то ребро  получило бы приращение
получило бы приращение 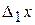 . Его значение определяется из соотношения
. Его значение определяется из соотношения  . Если бы действовала только сила
. Если бы действовала только сила 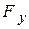 , то размеры параллелепипеда, перпендикулярные оси Y, сократились бы. В частности, ребро х при этом получило бы отрицательное приращение
, то размеры параллелепипеда, перпендикулярные оси Y, сократились бы. В частности, ребро х при этом получило бы отрицательное приращение  , которое можно вычислить по формуле
, которое можно вычислить по формуле 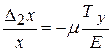 . Наконец, относительное приращение ребра под действием одной только силы было равно
. Наконец, относительное приращение ребра под действием одной только силы было равно 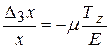 .
.

Рис. 8.4
Если бы все силы действовали одновременно, то согласно принципу суперпозиции малых деформаций результирующее удлинение ребра будет равно  . Аналогично вычисляются удлинения параллелепипеда, и вдоль остальных его ребер можно написать:
. Аналогично вычисляются удлинения параллелепипеда, и вдоль остальных его ребер можно написать:
 ,
,
 , (8.8)
, (8.8)
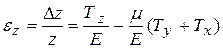 .
.
Рассмотрим частный случай, когда все натяжения 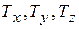 равны и отрицательны. В этом случае на параллелепипед со всех сторон действует постоянное давление
равны и отрицательны. В этом случае на параллелепипед со всех сторон действует постоянное давление  . Как видно из формул (8.8), все три относительные деформации
. Как видно из формул (8.8), все три относительные деформации 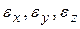 равны между собой и определяются выражением
равны между собой и определяются выражением
 (8.9)
(8.9)
Их можно выразить через относительные изменения объема параллелепипеда при деформации. Действительно, взяв логарифмические производные от обеих частей равенства  , получим
, получим 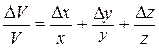 или
или 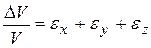 .
.
Поэтому формулу (8.9) можно представить в виде
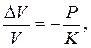 (8.10)
(8.10)
где постоянная К определяется выражением
 (8.11)
(8.11)
Эта постоянная называется модулем всестороннего сжатия.
Формула (8.11) применима к телам не только прямоугольной, но и произвольной форм. Для доказательства достаточно заметить, что произвольное тело можно разделить на малые части, каждая из которых имеет форму прямоугольного параллелепипеда. Эти части находятся под постоянным внешним давлением. Относительное изменение их объемов, а следовательно, и относительное изменение объема всего тела одинаковы и определяются формулой (8.10).
5. Энергия упругой деформации
Любое упруго деформированное тело обладает потенциальной энергией,так как изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.
Растяжение будем производить очень медленно, чтобы силу  , с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе
, с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе  . Тогда
. Тогда  где к, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна
где к, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна
 (8.12)
(8.12)
Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид
 , (8.13)
, (8.13)
если считать, что потенциальная энергия недеформированной пружины равна нулю.
Потенциальная энергия упруго деформированного стержня равна
где – объем стержня. Отношение энергии к тому объему , в котором она заключена, называется… Аналогично нетрудно получить, что плотность энергии деформации при сдвиге равна .Колебанияназываются свободными(или собственными),если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Для этих колебаний циклическую частоту обозначим как .
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания.За это время фаза колебания получает приращение 2л, т.е.  =
= , откуда
, откуда
 (11.5)
(11.5)
Величина, обратная периоду колебаний,
 (11.6)
(11.6)
т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний.Сравнивая (11.5) и (11.6), получим  .
.
Единица частоты – герц(Гц): 1 Гц – частота периодического процесса, при которой за 1с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s (соответственно скорость и ускорение):
 , (11.7)
, (11.7)
 , (11.8)
, (11.8)
т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (11.7) и (11.8) соответственно равны  и
и  . Фаза скорости (11.7) отличается от фазы величины (11.1) на
. Фаза скорости (11.7) отличается от фазы величины (11.1) на  , а фаза ускорения (11.8) отличается от фазы величины (11.1) на л. Следовательно,
, а фаза ускорения (11.8) отличается от фазы величины (11.1) на л. Следовательно,
– в моменты времени, когда х = 0, v приобретает наибольшие значения;
– когда же х достигает максимального отрицательного значения, то a приобретает наибольшее положительное значение (рис. 11.2).

| Рис.11.1 |
Из выражения (11.8) следует дифференциальное уравнение гармонических колебаний
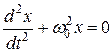 (11.9)
(11.9)
Решением этого уравнения являются выражения (11.1), (11.3) или (11.4).
2. Динамика колебательного движения
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается, например, формулой  .
.
В этом случае, как видно из формулы (11.8), при колебательном движении ускорение переменно. Следовательно, движение обусловлено действием переменной силы. Пусть под действием переменной силы  материальная точка массой m совершает гармоническое колебание с ускорением а. Тогда,
материальная точка массой m совершает гармоническое колебание с ускорением а. Тогда,  , так как
, так как  .
.
Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия). Эта сила стремится возвратить точку в положение равновесия, поэтому ее называют возвращающей силой. Возвращающей силой может быть, например, сила упругости, так как она тоже пропорциональна смещению и противоположна ему по знаку. Возвращающие силы могут иметь не только упругую, но и другую природу. В таких случаях они называются квазиупругими силами.
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
 (11.10)
(11.10)
или 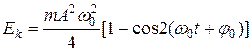 (11.11)
(11.11)
Потенциальная энергия материальнойточки, совершающей гармонические колебания под действием упругой силы F, равна
 (11.12)
(11.12)
или  (11.13)
(11.13)
Сложив (11.11) и (11.13), получим формулу для полной энергии:
 (11.14)
(11.14)
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.
Из формул (11.11) и (11.13) следует, что 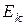 и
и  изменяются с частотой
изменяются с частотой 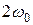 , т.е. с частотой, которая в два раза превышает частоту гармонического колебания.
, т.е. с частотой, которая в два раза превышает частоту гармонического колебания.
На рис. 11.3 представлены графики зависимости х, Ек =Т и Ер =II от времени. Так как средние значения <sin2a> = <cos2a> =1/2, то из формул (11.11), (11.13) и (11.14) следует, что средние значения 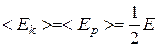 .
.

| Рис.11.3 |
3. Гармонический осциллятор. Пружинный, физический
и математический маятники
Гармоническим осцилляторомназывается система, совершающая колебания, описываемые уравнением вида
 (11.15)
(11.15)
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.
1. Пружинный маятник –это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы  , где k – коэффициент упругости, в случае пружины называемый жесткостью.
, где k – коэффициент упругости, в случае пружины называемый жесткостью.
Уравнение движения маятника 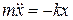 или
или 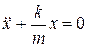
Из его решения следует, что пружинный маятник совершает гармонические колебания по закону  с циклической частотой
с циклической частотой
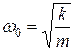 (11.16)
(11.16)
и периодом
 (11.17)
(11.17)
Формула (11.17) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела.
Потенциальная энергия пружинного маятника согласно (11.12) и (11.16) равна  .
.
2. Физический маятник– это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела (рис. 11.4).
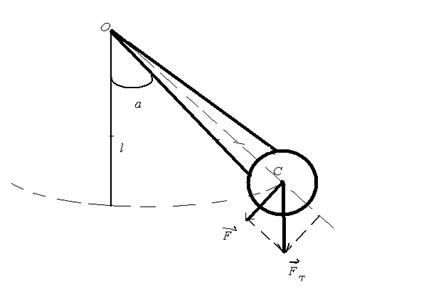
| Рис. 11.4 |
Пусть физический маятник совершает колебания вокруг неподвижной точки О. Обозначим массу маятника через m, длину маятника ОС, т.е. расстояние между точкой подвеса и центром масс маятника через  . Действуют две силы: сила тяжести
. Действуют две силы: сила тяжести  , приложенная к центру масс твердого тела С, и сила реакции опоры
, приложенная к центру масс твердого тела С, и сила реакции опоры  , приложенная к точке О.
, приложенная к точке О.
Если маятник отклонен из положения равновесия на некоторый угол а, то он под действием силы тяжести возвращается к положению равновесия, переходит его по инерции, отклоняется в противоположную сторону, затем опять переходит в положение равновесия и т.д. Центр тяжести маятника будет описывать дугу окружности. Возвращающая сила равна  (знак минус обусловлен тем, что направления
(знак минус обусловлен тем, что направления  и
и  всегда противоположны). При малых отклонениях (
всегда противоположны). При малых отклонениях ( )
) 
В соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы можно записать в виде
 (11.18)
(11.18)
где  – момент инерции маятника относительно оси, проходящей через точку О.
– момент инерции маятника относительно оси, проходящей через точку О.
Таким образом, уравнение движения физического маятника можно записать в виде  или
или
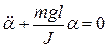 (11.19)
(11.19)
Обозначим  (11.20)
(11.20)
Получим уравнение
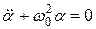 (11.21)
(11.21)
Оно идентично с (11.15). Следовательно, решение его известно:
 (11.22)
(11.22)
Из выражения (11.22) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой 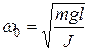 и периодом
и периодом
 (11.23)
(11.23)
В этой формуле  – приведенная длина физического маятника.
– приведенная длина физического маятника.
Точка О' на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качанийфизического маятника. Применяя теорему Штейнера, получим 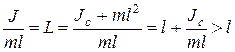 , т.е. 00' всегда больше ОС. Точка подвеса О и центр качаний О' обладают свойством взаимозаменяемости:если ось подвеса перенести в центр качаний, то точка О прежней оси подвеса станет новым центром качаний и период колебаний физического маятника не изменится.
, т.е. 00' всегда больше ОС. Точка подвеса О и центр качаний О' обладают свойством взаимозаменяемости:если ось подвеса перенести в центр качаний, то точка О прежней оси подвеса станет новым центром качаний и период колебаний физического маятника не изменится.
3. Математический маятник –это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.
Пусть длина маятника равна  . Тогда момент инерции математического маятника есть
. Тогда момент инерции математического маятника есть
 (11.24)
(11.24)
Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке – центре масс, то, подставив выражение (11.24) в формулу (11.23), получим выражение для периода малых колебаний математического маятника
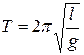 (11.25)
(11.25)
Сравнивая формулы (11.23) и (11.25), видим, что если приведенная длина L физического маятника равна длине  математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника –это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника –это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
4. Сложение гармонических колебаний одного направления
и одинаковой частоты. Биения
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Рассмотрим гармонические колебания одного направления и одинаковой частоты
 и
и  (11.26)
(11.26)
Очевидно, что уравнение результирующего колебания будет 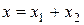 .
.
Подставим в него формулы (11.26), разложим их и введем обозначения
 (11.27)
(11.27)
 (11.28)
(11.28)
Здесь А и  – амплитуда и начальная фаза суммарного колебания. При этих обозначениях уравнение результирующего колебания имеет вид
– амплитуда и начальная фаза суммарного колебания. При этих обозначениях уравнение результирующего колебания имеет вид
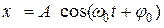 (11.29)
(11.29)
Из (11.29) видно, что результирующее колебание так же является гармоническим.
Для определения А и  решается система, состоящая из уравнений (11.27) и (11.28). Решая их, получим
решается система, состоящая из уравнений (11.27) и (11.28). Решая их, получим
 (11.30)
(11.30)
 (11.31)
(11.31)
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз  складываемых колебаний.
складываемых колебаний.
Проанализируем выражение (11.30) в зависимости от разности фаз  :
:
1) 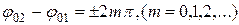 ,
,
тогда  т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
2)  ,
,
тогда 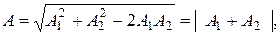 т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны 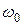 и
и  , причем
, причем  . Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:  и
и 
Складывая эти выражения и учитывая, что во втором сомножителе  , найдем
, найдем
 (11.32)
(11.32)
Получившееся выражение есть произведение двух колебаний. Так как  , то сомножитель, стоящий в скобках, почти не изменится, когда сомножитель
, то сомножитель, стоящий в скобках, почти не изменится, когда сомножитель 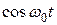 совершит несколько полных колебаний. Поэтому результирующее колебание х можно рассматривать как гармоническое с частотой
совершит несколько полных колебаний. Поэтому результирующее колебание х можно рассматривать как гармоническое с частотой 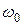 , а амплитуда изменится по следующему периодическому закону:
, а амплитуда изменится по следующему периодическому закону:
 (11.33)
(11.33)
Частота изменения  в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний:
в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний:  . Период биений
. Период биений 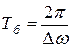 .
.
Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями – наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.
Любые сложные периодические колебания s = f(t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте
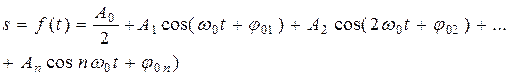 (11.34)
(11.34)
Представление периодической функции в виде (11.34) связывают с понятием гармонического анализа сложного периодического колебания,или разложения Фурье.
Члены ряда Фурье, определяющие гармонические колебания с частотами  называются первой(или основной), второй, третьей и т.д. гармоникамисложного периодического колебания.
называются первой(или основной), второй, третьей и т.д. гармоникамисложного периодического колебания.
5. Сложение взаимно перпендикулярных колебаний
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты  , происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты отсчета начальную фазу первого колебания возьмем равной нулю:
, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты отсчета начальную фазу первого колебания возьмем равной нулю:
 (11.35)
(11.35)
Разность фаз обоих колебаний равна  , A и В – амплитуды складываемых колебаний.
, A и В – амплитуды складываемых колебаний.
Уравнение траектории результирующего колебания находится исключением из выражений (11.35) параметра t. Запишем складываемые колебания в виде 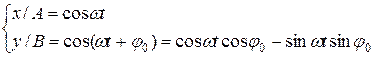
После несложных преобразований получим уравнение эллипса:
 (11.36)
(11.36)
Оси эллипса ориентированы относительно координатных осей произвольно. Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз. Рассмотрим некоторые частные случаи, представляющие физический интерес:
1)  . В данном случае эллипс вырождается в отрезок прямой
. В данном случае эллипс вырождается в отрезок прямой
 (11.37)
(11.37)
где знак плюс соответствует нулю и четным значениям т (рис. 11.5, а), знак минус – нечетным значениям т (рис. 11.5, б). Результирующее колебание является гармоническим колебанием с частотой  и амплитудой
и амплитудой  , совершающимся вдоль прямой (11.37), составляющей с осью х угол
, совершающимся вдоль прямой (11.37), составляющей с осью х угол 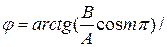
В данном случае имеем дело с линейно поляризованными колебаниями.
2)  .Вданном случае уравнение примет вид
.Вданном случае уравнение примет вид
 (11.38)
(11.38)

| 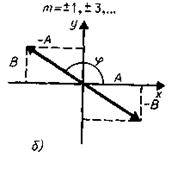
| 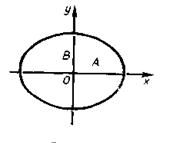
|
| Рис.11.5, а | Рис.11.5, б | Рис.11.5, в |
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис.11.5, в). Кроме того, если А=В, то эллипс (11.38) вырождается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу.Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 11.6 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху).

| Рис.11.6 |
Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу – широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
6. Свободные затухающие колебания
Рассмотрим свободные затухающие колебания– колебания, амплитуда которых из-за потерь энергии реальной колебательной системы с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах.
Закон затухающих колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы– идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука). Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.
Дифференциальное уравнение свободных затухающих колебанийлинейной системы задается в виде
 , (11.39)
, (11.39)
где s – колеблющаяся величина, описывающая тот или иной физический процесс, 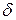 = const – коэффициент затухания,
= const – коэффициент затухания, 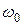 – циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при
– циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при  (при отсутствии потерь энергии) называется собственной частотойколебательной системы.
(при отсутствии потерь энергии) называется собственной частотойколебательной системы.
Решение уравнения (11.39) рассмотрим в виде
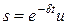 (11.40)
(11.40)
где u = u(t). После нахождения первой и второй производных выражения (11.40) и подстановки их в (11.39) получим
 (11.41)
(11.41)
Решение этого уравнения зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:
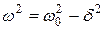 (11.42)
(11.42)
Тогда получим уравнение типа (11.4):  .
.
Решением его является функция  .
.
Таким образом, решение уравнения (11.39) в случае малых затуханий есть
 (11.43)
(11.43)
где 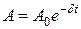 , (11.44)
, (11.44)
– амплитуда затухающих колебаний, – начальная амплитуда.
– начальная амплитуда.
Промежуток времени 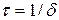 , в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.
, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины. Тогда период затухающих колебаний равен 
Если A(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение  называется декрементом затухания,а его логарифм
называется декрементом затухания,а его логарифм
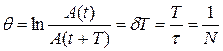 (11.45)
(11.45)
– логарифмическим декрементом затухания;N – число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная для данной колебательной системы величина.
Для характеристики колебательной системы пользуются понятием добротностиQ, которая при малых значениях логарифмического декремента равна
 (11.46)
(11.46)
(так как затухание невелико ( ), то Т принято считать равным T0).
), то Т принято считать равным T0).
Из формулы (11.46) следует, что добротность пропорциональна числу колебаний N, совершаемых системой за время релаксации.
Применим выводы, полученные для свободных затухающих колебаний линейных систем, для механических колебаний. В качестве примера рассмотрим пружинный маятник.
Для пружинного маятника массой т, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т.е.  где
где  – коэффициент сопротивления;знак минус указывает на противоположные направления силы трения и скорости.
– коэффициент сопротивления;знак минус указывает на противоположные направления силы трения и скорости.
При данных условиях закон движения маятника будет иметь вид
 (11.47)
(11.47)
Используя формулу 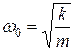 и принимая, что коэффициент затухания
и принимая, что коэффициент затухания
 , (11.48)
, (11.48)
получим дифференциальное уравнение затухающих колебаний маятника: 
Из предыдущих выражений вытекает, что маятник колеблется по закону
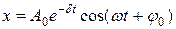 (11.49)
(11.49)
с частотой  .
.
Добротность пружинного маятника  .
.
При увеличении коэффициента затухания 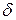 период затухающих колебаний растет и при
период затухающих колебаний растет и при  обращается в бесконечность, т.е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда
обращается в бесконечность, т.е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда  . Процесс не будет колебательным. Он называется апериодическим.
. Процесс не будет колебательным. Он называется апериодическим.
7. Вынужденные колебания
Чтобы в реальной механической колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью периодически действующей вынуждающей силы, изменяющейся по гармоническому закону:
 (11.50)
(11.50)
С учетом силы (11.50) закон движения для пружинного маятника запишется в виде .
.
Используя соответствующие обозначения, придем к уравнению
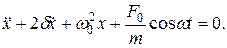 (11.51)
(11.51)
Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями.
(11.52) Частное решение этого уравнения будем искать в виде Найдем производные для : . Подставляя выражение для и его производных в уравнение (11.52), получим.
Произведя соответствующие преобразования, получаем релятивистский закон сложения скоростей специальной теории относительности:

| 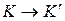
|
 , ,
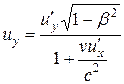 , ,
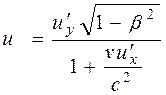
|  , ,
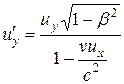 , (13.13) , (13.13)
 . .
|
Если материальная точка движется параллельно оси х, то скорость и относительно системы К совпадает с их, а скорость и' относительно К' – с и'х. Тогда закон сложения скоростей примет вид
 ,
,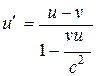 (13.14)
(13.14)
Легко убедиться в том, что если скорости v, и' и и малы по сравнению со скоростью света с, то формулы (13.14) и (13.13) переходят в закон сложения скоростей в классической механике. Таким образом, законы релятивистской механики в предельном случае для малых скоростей (по сравнению со скоростью света) переходят в законы классической физики, которая, следовательно, является частным случаем механики Эйнштейна для малых скоростей.
Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна. Действительно, если  , то формула (13.14)) примет вид
, то формула (13.14)) примет вид  (аналогично можно показать, что при
(аналогично можно показать, что при  скорость и' также равна с). Этот результат свидетельствует о том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна.
скорость и' также равна с). Этот результат свидетельствует о том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна.
Докажем также, что если складываемые скорости сколь угодно близки к скорости света с, то их результирующая скорость будет всегда меньше или равна с. В качестве примера рассмотрим предельный случай u' = v = c. После подстановки в формулу (13.14) получим и = с. Таким образом, при сложении любых скоростей результат не может превысить скорости света с в вакууме. Скорость света в вакууме есть предельная скорость, которую невозможно превысить.
5. Интервал между событиями
Преобразования Лоренца и следствия из них приводят к выводу об относительности длин и промежутков времени, значение которых в различных системах отсчета разное. В то же время относительный характер длин и промежутков времени в теории Эйнштейна означает относительность отдельных компонентов какой-то реальной физической величины, не зависящей от системы отсчета, т.е. являющейся инвариантной по отношению к преобразованиям координат. В четырехмерном пространстве Эйнштейна, в котором каждое событие характеризуется четырьмя координатами  , такой физической величиной является интервал между двумя событиями:
, такой физической величиной является интервал между двумя событиями:
 , (13.15)
, (13.15)
где 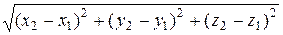 – расстояние между точками обычного трехмерного пространства, в которых эти события произошли. Введя обозначение
– расстояние между точками обычного трехмерного пространства, в которых эти события произошли. Введя обозначение 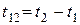 ,
,  , покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив
, покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив 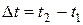 ,
, ,
,  ,
, 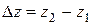 , выражение (13.15) можно записать в виде
, выражение (13.15) можно записать в виде 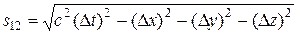 .
.
Интервал между теми же событиями в системе К' равен
 (13.16)
(13.16)
Согласно преобразованиям Лоренца (13.8),
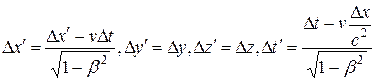 .
.
Подставив эти значения в (13.16), после элементарных преобразований получим, что  , т.е.
, т.е.  .
.
Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-временные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря на относительность длин и промежутков времени, течение событий носит объективный характер и не зависит от системы отсчета.
Теория относительности, таким образом, сформулировала новое представление о пространстве и времени, обобщенное далее в диалектическом материализме. Пространственно-временные отношения являются не абсолютными величинами, как утверждала механика Галилея-Ньютона, а относительными. Следовательно, представления об абсолютном пространстве и времени являются несостоятельными. Кроме того, инвариантность интервала между двумя событиями свидетельствует о том, что пространство и время органически связаны между собой и образуют единую форму существования материи – пространство-время. Пространство и время не существуют вне материи и независимо от нее.
Дальнейшее развитие теории относительности (общая теория относительности,или теория тяготения)показало, что свойства пространства-времени в данной области определяются действующими в ней полями тяготения. При переходе к космическим масштабам геометрия пространства-времени не является евклидовой (т.е. не зависящей от размеров области пространства-времени), а изменяется от одной области к другой в зависимости от концентрации масс в этих областях и их движения.
6. Основной закон релятивистской динамики материальной точки
Согласно представлениям классической механики, масса тела есть величина постоянная. Однако в конце XIX столетия на опытах с быстро движущимися электронами было установлено, что масса тела зависит от скорости его движения, а именно возрастает с увеличением скорости по закону
 , (13.17)
, (13.17)
где  – масса покояматериальной точки, т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой материальная точка находится в покое; с – скорость света в вакууме; т – масса точки в системе отсчета, относительно которой она движется со скоростью и. Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
– масса покояматериальной точки, т.е. масса, измеренная в той инерциальной системе отсчета, относительно которой материальная точка находится в покое; с – скорость света в вакууме; т – масса точки в системе отсчета, относительно которой она движется со скоростью и. Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона  оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.
Основной закон релятивистской динамикиматериальной точки имеет вид
 (13.18)
(13.18)
или
 (13.19)
(13.19)
где 
 ) (13.20)
) (13.20)
– релятивистский импульсматериальной точки.
Отметим, что уравнение (13.20) внешне совпадает с основным уравнением ньютоновской механики. Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (13.20). Таким образом, уравнение (13.20) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.
В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса:релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выражение для импульса.
Анализ формул (13.17) – (13.19) показывает, что при скоростях, значительно меньших скорости света, уравнение (13.20) переходит в основной закон классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально переход осуществляется при 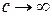 ). Таким образом, классическая механика – это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
). Таким образом, классическая механика – это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
Экспериментальное доказательство зависимости массы от скорости (13.20) является подтверждением справедливости специальной теории относительности.
7. Взаимосвязь массы и энергии
Найдем кинетическую энергию релятивистской частицы (материальной точки). Раньше было показано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:
 или dT=Fdr(13.21)
или dT=Fdr(13.21)
Учитывая, что dr = v dt, и подставив в (13.21) выражение (13.20), получим  .
.
Преобразовав данное выражение с учетом того, что vdv =vdv, а также учитывая формулу (13.20), придем к выражению
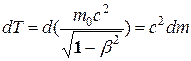 (13.22)
(13.22)
т.е. приращение кинетической энергии частицы пропорционально приращению ее массы.
Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя т0, то, проинтегрировав (13.22), получим
Т = (т – т0)с (13.23)
или кинетическая энергия релятивистской частицы имеет вид
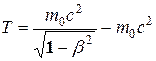 (13.24)
(13.24)
Разлагая в ряд 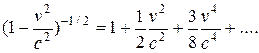 , пренебрегая членами второго порядка малости при v<<c, выражение (13.24) переходит в классическое:
, пренебрегая членами второго порядка малости при v<<c, выражение (13.24) переходит в классическое:  .
.
А. Эйнштейн обобщил положение (13.22), предположив, что оно справедливо не только для кинетической энергии материальной точки, но и для полной энергии, а именно: любое изменение массы 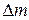 сопровождается изменением полной энергии материальной точки
сопровождается изменением полной энергии материальной точки
 (13.25)
(13.25)
Отсюда А. Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:
 (13.26)
(13.26)
Уравнение (13.26), равно как и (13.25), выражает фундаментальный закон природы – закон взаимосвязи (пропорциональности) массы и энергии:полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле.
Учитывая выражение (13.23), закон (13.26) можно записать в виде Е = т0 с2 + Т, откуда следует, что покоящееся тело (Т = 0) также обладает энергией Е0 = т0с2, называемой энергией покоя.Классическая механика энергию покоя Е0 не учитывает, считая, что при v =0 энергия покоящегося тела равна нулю.
В силу однородности времени в релятивистской механике, как и в классической, выполняется закон сохранения энергии:полная энергия замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Из формул (13.26) и (13.20) найдем релятивистское соотношение между полной энергией и импульсом частицы:
 ,
,  (13.27)
(13.27)
Возвращаясь к уравнению (13.26), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко всем формам энергии, т.е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса
т = Е/с2, (13.28)
и, наоборот, со всякой массой связана определенная энергия (13.20).
Рассматривая выводы специальной теории относительности, видим, что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений. Масса тела не остается постоянной величиной, а зависит от скорости тела; длина тел и длительность событий не являются абсолютными величинами, а носят относительный характер; наконец, масса и энергия оказались связанными друг с другом, хотя они и являются качественно различными свойствами материи.
Эту ломку укоренившихся представлений некоторые философы пытались использовать для распространения двух разновидностей идеализма: энергетизма и философского релятивизма. Первая из этих теорий рассматривала возможность преобразования массы в энергию и, наоборот, энергии в массу, доказывая «эквивалентность материи и энергии». Закон взаимосвязи массы и энергии действительно утверждает, что любые превращения энергии тела сопровождаются изменениями его массы, однако при этом масса не «переходит в энергию». Закон взаимосвязи массы и энергии является подтверждением неразрывности материи и движения – одного из основных положений диалектического материализма.
Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи – пространство-время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи.
Контрольные вопросы
1. В чем физическая сущность механического принципа относительности?
2. В чем заключается правило сложения скоростей в классической механике?
3. 3.Каковы причины возникновения специальной теории относительности?
4. В чем заключаются основные постулаты специальной теории относительности?
5. Зависит ли от скорости движения системы отсчета скорость тела? скорость света?
6. Запишите и прокомментируйте преобразования Лоренца. При каких условиях они переходят в преобразования Галилея?
7. Какой вывод о пространстве и времени можно сделать на основе преобразований Лоренца?
8. 8.Одновременны ли события в системе К', если в системе К они происходят в одной точке и одновременны? в системе А" события разобщены, но одновременны? Обосновать ответ.
9. Какие следствия вытекают из специальной теории относительности для размеров тел и длительности событий в разных системах отсчета? Обосновать ответ.
10. При какой скорости движения релятивистское сокращение длины движущегося тела составит 25%?
11. В чем состоит «парадокс близнецов» и как его разрешить?
12. В чем заключается релятивистский закон сложения скоростей? Как показать, что он находится в согласии с постулатами Эйнштейна?
13. Как определяется интервал между событиями? Доказать, что он является инвариантом при переходе от одной инерциальной системы отсчета к другой.
14. Какой вид имеет основной закон релятивистской динамики материальной точки? Чем он отличается от основного закона ньютоновской механики?
15. В чем заключается закон сохранения релятивистского импульса? релятивистской массы?
16. Как выражается кинетическая энергия в релятивистской механике?
17. При каком условии релятивистская формула для кинетической энергии переходит в классическую формулу?
18. Сформулируйте и запишите закон взаимосвязи массы и энергии. В чем его физическая сущность? Приведите примеры его экспериментального подтверждения.
Учебное издание
Фатыхов Миннехан Абузарович
Механика
Редактор Н.Р. Ахтямова Технический редактор И.В. Пономарев– Конец работы –
Используемые теги: Уфа, 20080.037
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Уфа 2008
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов