Доказательство

<=

Пусть граф G непланарен, тогда он cодержит подграф Н, гомеоморфный либо графу К5, либо графу К3,3(по теореме Куратовского). Стягивая ребра подграфа Н, инцидентные вершинам степени 2, мы получим граф К5 или граф К3,3.

=>

Предположим, что G содержит подграф Н, стягиваемый к К3,3 и что вершина v графа К3,3 получена стягиванием подграфа Нv графа Н. В графе К3,3 вершина v инцидентна трём (не обязательно различным) рёбрам e1, e2, e3; как рёбра из Н они инцидентны трём вершинам v1, v2, v3 подграфа Нv. Если v1, v2, v3 различны , то можно найти вершину w из Нv и три простые цепи, ведущие из w в эти вершины и пересекающиеся только в w.(Можно проделать аналогичное построение и в том случае, когда не все вершины различны: при этом простые цепи вырождаются в отдельные вершины).

5.4 Хроматическое число графа.

Граф называется р-хроматическим, если его вершины можно раскрасить р красками так, чтобы смежные вершины не были раскрашены одинаково. Наименьшее значение р называется хроматическим числом графа и обозначается g(G). Доказано, что хроматическое число всякого плоского графа (графа, который можно изобразить на плоскости без пересечений ребер вне вершин) не превышает 5 (остается нерешенной проблема четырех красок: всякую политическую карту мира можно раскрасить четырьмя красками, то есть всякий плоский граф является 4-хроматическим)

Минимальное число красок для раскрашивания ребер графа без одинакового окрашивания смежных ребер называют хроматическим классом графа.

 

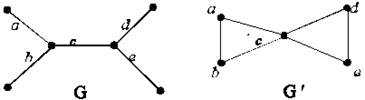
Хроматический класс графа G совпадает с хроматическим числом графа G', который получается из G заменой ребер вершинами с сохранением смежности .

Пусть графы G и H соответственно p+1- и q+1-хроматические. Граф G+H является r+1-хроматическим, где

(символ Е определяет поразрядное суммирование двоичных представлений чисел с приведение по модулю 2; например, 5Е6=3).

Пусть графы G и H соответственно p и q -хроматические. Граф GґH является r-хроматическим, где r = min(p,q).

 

5.5 Раскраска графов

Определение 1.Подмножество V1 Í V вершин графа G = (V, E) называется независимым, если никакие две вершины из V1 не соединяются ребром.

Определение 2.Пусть есть некоторое множество C = {C1, C2, …, Cm} — множество

цветов. Тогда раскраской графа G = (V, E) (вершинной) называется любое отображение

φ: V ® C. Раскраска называется правильной, если для любого цвета вершины этого цвета об-

разуют независимое множество.

Пример: На следующем рисунке показана правильная раскраска.

 

 

Красный Синий

 

 

Зеленый Зеленый

 

Синий Красный

Лемма :В планарном графе без петель и кратных рёбер существует вершина v:

deg v £5.

Доказательство:Пусть G — планарный граф с p вершинами и q рёбрами. Пусть в G нет вершин степени 0 и 1. Тогда q £ 3(p – 2) < 3p. Пусть dmin — минимальная степень вершин в

G. Тогда получаем

p

6 p >2q =å deg vi³pdmin

i=1

 

 

Отсюда dmin < 6, то есть dmin £ 5. Лемма доказана.

 

Теорема :Вершины любого планарного графа можно правильно раскрасить в не более чем 5 цветов.

Доказательство:Проведём индукцию по числу вершин p.

1) Базис индукции: p = 1 — очевидно.

2) Пусть для p < p0 утверждение справедливо и пусть G = (V, E) — планарный граф с

|V| = p0. Согласно лемме 2 в G есть вершина v степени не более 5. Рассмотрим укладку на

плоскости графа G без пересечения рёбер. Удалим из G вершину v и все инцидентные ей

рёбра. Получим планарный граф G1 с числом вершин p0 – 1. По предположению индукции

его вершины можно правильно раскрасить в 5 цветов C1, C2, C3, C4, C5. Пусть в G вершина v

смежна с v1, v2, …, vk, где k £5. Возможны два случая:

a) Среди цветов вершин v1, v2, …, vk в G нет цвета Ci (1 £i £5). Тогда вершине v

припишем цвет Ci и получим правильную раскраску графа G в 5 цветов.

b) Степень вершины v равна 5 и среди вершин v1, v2, …, v5 в G1 есть все 5 цветов.

Без ограничения общности будем считать, что в укладке графа G рёбра (v, v1),

(v, v2), (v, v3), (v, v4), (v, v5) выходят из v в порядке по часовой стрелке и что

C (vi) = Ci, i = 1, …, 5. Пусть A — множество всех вершин в G1, до которых можно

дойти из v1 по рёбрам графа G1, используя только вершины цветов C1 и C3.

Возможны два варианта:

i) v3ÏA. Тогда в A поменяем цвета C1 ® C3, C3 ® C1. Так как вершины из A не смежны с другими вершинами цветов C1 и C3, то останется правильная раскраска и среди v1, v2, v3, v4, v5 не будет цвета C1. Тогда вершине v припишем цвет C1.

ii) v3ÎA. Это значит, что в A есть цепь из v1 в v3, все вершины которой имеют цвета C1 и C3. Эта цепь вместе с рёбрами (v3, v) и (v, v1) образует цикл в G, причём вершины v2 и v4 лежат по разные стороны от этого цикла. Это значит, что из v2 нельзя пройти в v4 в графе A только по вершинам цветов C2 и C4. Пусть B — множество всех вершин в G, до которых можно дойти из v2 по рёбрам графа G, используя только вершины цветов C2 и C4. Тогда v4ÏB и далее поступаем как в i).

В любом случае вершины графа G можно правильно раскрасить в не более чем 5 цветов,

и теорема доказана.

Теорема:

Трех красок мало.

Доказательство:

1

4 Пример доказывает, что 3-х красок мало

2 3

Утверждение: В графе G найдется вершина степени не больше 5.

Доказательство. Предположим, что это не так, т.е. существует планар-

ный граф, степень любой вершины которого не меньше шести. Для каждой

вершины подсчитаем выходящие из нее ребра; складывая эти числа по всем

вершинам, получим удвоенное число ребер (т.к. каждое ребро соединяет две

вершины). Таким образом, для нашего графа 2q≥ 6p. С другой стороны,

подсчитаем число ребер на границе каждой области, на которые граф делит

плоскость; поскольку в каждом цикле графа не менее трех ребер, получим

2q ≥ 3r. Умножая последнее неравенство на 3 и складывая с предыдущим,

получим 6q ≥6p+ 6rили 6(p + r - q) ≤0, что противоречит формуле

Следует сказать, что американскими математиками была доказана теорема, о том, что четырех красок достаточно. Однако, в этом доказательстве есть шаги, связанные с очень большими переборами вариантов, выполненные с использованием компьютера. Так что с точки зрения «пуританской» математики можно считать, что теорема пока не доказана…

 

Задача: На предприятии планируется выполнить 8 работ: v₁,v₂,…v₈. Для выполнения этих работ необходимы механизмы а₁,а₂,…,а₆. Использование механизмов для проведения каждой из работ определяется следующей таблицей Т:

 

Работа механ.	v1	v2	v3	v4	v5	v6	v7	v8
a1	+		+				+	+
a2		+		+
a3			+			+	+
a4	+	+		+	+
a5			+		+			+
a6					+	+		+

 

Никакой из механизмов не может быть занят одновременно на двух работах. Все работы выполняются за одно и тоже время t. Как распределить механизмы, чтобы суммарное время выполнения всех работ было наименьшим?

Решение: Рассмотрим граф G, множество вершин V которого состоит из планируемых работ, т.е. V={v₁,v₂,…,v₈}. Вершины v_i и v_j (при i≠j) соединим ребром в том и только в том случае, когда существует хотя бы один механизм, который используется при выполнении и той и другой работы. Мы получим граф, изображенный на рис.

рис.

Граф содержит четырехэлементный полный подграф {v₁,v₂,v₄,v₅}, поэтому для правильной раскраски графа потребуется, как минимум четыре краски. Раскрасим эти вершины так, как показано на рис. Далее, вершины v₃ и v₈ смежны между собой и смежны вершинам v₁ и v₅, раскрашенным первой и четвертой красками. Одна из этих вершин, следовательно, должна быть раскрашена второй, другая третьей красками. Осталось раскрасить вершины v₆ и v₇. Вершину v₆ красим первой, а v₇ – четвертой красками. Мы получили правильную раскраску графа четырьмя красками. Следовательно, все работы можно выполнить за время 4t по такому графику: сначала выполняются работы v₁ и v₆, затем v₂ и v₈, v₃ и v₄ и, наконец, v₅ и v₇.