Задача.

Шесть человек участвуют в шахматном турнире, который проводится в один круг, то есть каждый шахматист встречается со всеми участниками по одному разу. Нужно доказать, что среди них всегда найдутся три участника турнира, которые провели уже все встречи между собой или еще не сыграли друг с другом ни одной партии.

Решение. Любые два участника турнира находятся между собой в одном из двух отношений: они либо уже сыграли между собой, либо еще не сыграли.

 

Каждому участнику поставим в соответствие вершину графа. Соединим вершины попарно ребрами двух цветов. Пусть ребро красного цвета (обозначенное цифрой 1) означает, что двое уже сыграли между собой, а синего (пронумерованное цифрой 2) — что не сыграли. Получим полный граф с шестью вершинами и ребрами двух цветов.

Теперь для решения задачи достаточно доказать, что в таком графе обязательно найдется "треугольник" с одноцветными сторонами.

Каждая вершина полученного графа принадлежит пяти ребрам. Скольким шахматистам одного цвета может принадлежать произвольная вершина такого графа? Пять принадлежащих одной вершине ребер могут быть окрашены без учета порядка следующим образом: 22222, 12222, 11222, 11122, 11112, 11111. То есть каждая вершина принадлежит, по меньшей мере, трем шахматистам одного цвета. Пусть, например, вершина va принадлежит трем ребрам красного цвета:

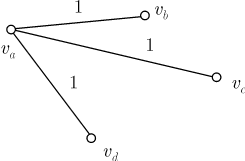
Какого цвета ребра могут соединять вершины vb ,vc и vd? Если хотя бы одно из них окажется красным, как на рисунке,

то получится треугольник с красными сторонами. Если же все эти ребра синие, как на рисунке,

то они вместе образуют "треугольник" с синими сторонами.

Задача решена. Рассмотрены все возможности. В каждом случае нашлись три шахматиста, или все сыгравшие между собой по одной партии, или не сыгравшие между собой ни одной партии.

5.6 Цикломатическое число.

 

Можно рассматривать не просто графы, а мультиграфы (X,U), где Х - множество вершин, U - множество ребер (в отличие от обычного графа каждая пара вершин может быть связана более чем одним ребром). Например, формулы органической химии - типичный пример мультиграфа.

 

Если взять мультиграф G с n вершинами, m ребрами и p компонентами связности, то число ν(G)=m-n+ p называется цикломатическим числом мультиграфа. (ρ(G)=n- p)

 

Теорема 1: Пусть G’ – мультиграф, полученный из мультиграфа G добавлением нового ребра между вершинами a и b; если a и b совпадают или могут быть соединены цепью в G, то: ρ(G’) = ρ(G); ν(G’) = ν(G) + 1; В противном случае: ρ(G’) = ρ(G) + 1; ν(G’) = ν(G);

Доказательство: (Непосредственно).

Следствие: ρ(G) ≥ 0; ν(G) ≥ 0;

Доказательство: Для графа G, образованного всеми вершинами V, но без ребер имеем:

ρ(G) = 0; ν(G) = 0;

Каждое добавление ребра либо увеличивает ρ, не меняя ν, либо увеличивает ν, не меняя ρ. Таким образом, в процессе построения графа G числа ρ и ν могут только возрастать.

 

Удобно следующим образом отождествлять циклы мультиграфа с векторами:

придадим каждому ребру графа G произвольную ориентацию; если цикл μ проходит через ребро u_k в направлении его ориентации r_k раз и в противоположном направлении s_k раз, то полагаем c^k = r_k - s_k .

Вектор (c¹, c², …, c^k, … , c^m) m-мерного пространства R^m называют вектором-циклом, соответствующим циклу μ и обозначают через .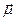

Циклы μ, μ’, μ’’ называют независимыми, если соответствующие им векторы линейно независимы. Это свойство не зависит от выбора ориентации ребер.

 

Теорема 2: Цикломатическое число ν(G) мультиграфа G равно наибольшему количеству независимых циклов.
Доказательство: Рассмотрим граф без ребер, образованный всеми вершинами G и, добавляя к нему ребро за ребром, построим данный мультиграф G. В силу теоремы 1 цикломатическое число увеличивается на единицу, когда добавление ребра приводит к образованию новых циклов и не меняется в противном случае. Пусть перед добавлением ребра u_k уже имелась база, состоящая из независимых циклов μ₁, μ₂, … и что добавление u_k повлекло за собой возникновение циклов ν₁, ν₂, … . Если среди новых циклов есть простые:

пусть, например, ν₁ – простой. ν₁^k = 1. Очевидно, ν₁ не может линейно выражаться через μ_i (μ₁ ^k = μ₂ ^k = … = 0). C другой стороны, ν₂ (и аналогично ν_3, …) можно линейно выразить через ν₁, μ₁, μ₂ … Действительно, вектор ν₂ - ν₂ ^k ν₁ соответствует некоторому циклу, не содержащему ребро u_k (этот цикл получается из ν₂ заменой ребра u_k оставшейся частью ν₁ с измененным направлением обхода) и значит линейно выражается через μ₁, μ₂ … Таким образом, каждый шаг, увеличивающий на единицу цикломатическое число, в то же время на единицу увеличивает наибольшее количество независимых циклов.

 

Следствие 1: Граф G не имеет циклов тогда и только тогда, когда ν(G) = 0.

Следствие 2: Граф G имеет один единственный цикл тогда и только тогда, когда ν(G) = 1.

6 Представления графов в виде матрицы смежности

(и матрицы инцидентности для ориентированных графов).

Информация о структуре графа может быть задана при помощи матрицы бинарного состоящей из нулей и единиц.

Пусть – граф, в котором множество вершин имеет 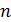элементов: .

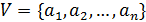Матрицей смежности графа называется матрица порядка 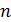, определенная следующим образом:

Для ориентированных графов:

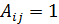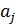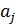Если , то вершина называется последователем вершины , а – предшественником . Вершины и 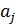называются смежными, ес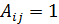ли или .

Если граф - мультиграф, то в матрице смежности элемент по определению равен числу дуг, исходящих из вершины и заходящих в вершину .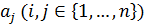

Пример:

Граф , изображенный на рисунке имеет матрицу смежности:

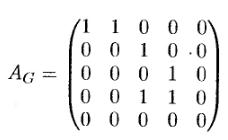
Если - граф без петель, то в матрице смежности по главной диагонали стоят нулевые элементы:

6.1Теорема:

Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременными перестановками строк и столбцов (т.е. одновременно с перестановкой -й и -й строк переставляются 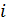-й и -й столбцы).

Согласно этой теореме по матрице смежности граф восстанавливается однозначно с точностью до изоморфизма.

В мультиграфе дуга представленная упорядоченной парой 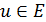называется инцидентной по вершине , если эта дуга начинается или заканчивается вершиной

, , то матрицей инцидентности 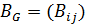мультиграфа называется матрица размерности 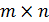, определяемая по следующему правилу:

Пример:

Мультиграф , изображенный на рисунке, имеет матрицу инцидентности: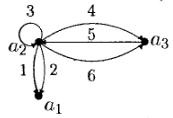

Определение:

Мультиграфы и и 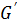изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановками строк и столбцов.

Развернуть

Открыть в широком формате